Imię i nazwisko: Tomasz Wydmański	ĆWICZENIE ,,M7” WYZNACZANIE LICZBY REYNOLDSA
Kierunek i rok: Fizyka I rok	Ocena z kolokwium: ....................................... data ....................... podpis...........................	Ocena ze sprawozdania: ....................................... data ....................... podpis...........................	Ocena końcowa: ....................................... data ....................... podpis...........................
Nazwisko prowadzącego zajęcia: dr Z.Olesik

I.WSTĘP TEORETYCZNY

Przepływ płynów:

Jednym ze sposobów opisu ruchu płynu jest podzielenie płynu na nieskończenie małe elementy objętości, które możemy nazwać cząstkami płynu, i śledzenie ruchu każdej z tych cząstek. Jest to ogromne zadanie. Musielibyśmy przypisać każdej takiej cząstce współrzędne x, y, z i określić je jako funkcje czasu t. Dla cząstki płynu, która w chwili t₀ znajdowała się w punkcie x₀, y₀, z₀, współrzędne x, y, z w chwili t byłyby okreś1one przez funkcje x(x₀, y₀, z₀, t₀, t), y(x₀, y₀, z₀, t₀, t) i z(x₀, y₀, z₀, t₀, t) służące następnie do opisu płynu. Takie postępowanie, rozwinięte po raz pierwszy przez Josepha Louisa Lagrange'a (1736-1813), jest bezpośrednim uogólnieniem pojęcia mechaniki punktów materialnych.

Istnieje inne podejście, rozwinięte przez Leonharda Eulera (1707—1783), które w większości wypadków jest bardziej wygodne. Rezygnujemy w nim z prób opisania historii każdej cząstki płynu i zamiast tego określamy gęstość i prędkość płynu w każdym punkcie przestrzeni oraz w każdej chwili czasu. Ruch płynu będzie opisywany przez podanie gęstości ρ(x, y, z, t) oraz prędkości v(x, y, z, t) w punkcie (x, y, z) i w czasie t. W ten sposób koncentrujemy naszą uwagę na tym, co się dzieje w pewnym określonym punkcie przestrzeni oraz w pewnym określonym czasie, a nie na tym, co się dzieje z pewną określona cząstką. Jakakolwiek wielkość używana do opisu stanu płynu, na przykład ciśnienie p, będzie miała określoną wartość w każdym punkcie przestrzeni i w każdej chwili czasu. Chociaż przy takim opisie płynu koncentrujemy się na punkcie przestrzeni, a nie na cząstce płynu, to jednak nie możemy pominąć, przynajmniej dla krótkich przedziałów czasu dt, śledzenia samych cząstek. Do cząstek tych przecież, a nie do punktów przestrzeni, stosuje się prawa mechaniki. W celu zrozumienia istoty uproszczeń, które będziemy stosowali, rozważmy na początku pewne ogólne własności.

­1. Przepływ być ustalony (laminarny) albo nieustalony. Mówi się, że ruch płynu jest ustalony, kiedy prędkość płynu v jest w dowolnie wybranym punkcie stała w czasie. Oznacza to, że w dowolnym punkcie przepływu ustalonego prędkość każdej przechodzącej przez ten punkt cząstki płynu jest zawsze taka sama. W pewnym innym punkcie cząstka może poruszać się z inną prędkością, ale każda następna cząstka przechodząca przez ten drugi punkt zachowuje się w nim zupełnie tak samo, jak zachowywała się cząstka pierwsza.

Warunki takie mogą być osiągnięte przy niskich prędkościach przepływu; przykładem takiego ruchu jest łagodnie płynący strumyk. W przepływie nieustalonym, zachodzącym na przykład w ujściach rzek podczas przypływu morskiego, prędkości v są funkcją czasu. W przypadku przepływu turbulentnego, jaki powstaje w wodospadach, prędkości zmieniają się bezładnie od punktu do punktu, a także w miarę upływu czasu.

2. Przepływ może być wirowy lub bezwirowy. Przepływ jest bezwirowy wtedy, gdy w żadnym punkcie element płynu nie ma względem tego punktu wypadkowej prędkości kątowej. Możemy sobie wyobrazić małe kółko z łopatkami zanurzone w poruszającym się płynie. Ruch płynu jest bezwirowy, gdy kółko nie obraca się podczas ruchu; w przeciwnym razie ruch jest wirowy. Ruch różnego rodzaju wirów jest przepływem wirowym.

3. Przepływ może być ściśliwy lub nieściśliwy. Zazwyczaj można przyjmować, że przepływ cieczy jest nieściśliwy. Jednak nawet bardzo ściś1iwy gaz może czasami podlegać nieistotnym zmianom gęstości. Przepływ jego jest wtedy praktycznie biorąc nieściśliwy. Takim przykładem prawie nieściśliwego przepływu jest ruch powietrza względem skrzydeł samolotu, podczas lotu z prędkością dużo mniejszą od prędkości głosu w powietrzu. W takich wypadkach gęstość jest stała, niezależna od x, y, z oraz t, i w związku z tym matematyczny opis przepływu jest znacznie uproszczony.

4.Wreszcie przepływ może być lepki lub nielepki. Lepkość w ruchu płynów jest odpowiednikiem tarcia w ruchu ciał stałych. W wielu przypadkach, takich jak zagadnienia smarowania, lepkość jest bardzo istotną cechą. Czasem jest jednak do pominięcia. Lepkość wywołuje pojawienie się sił stycznych między warstwami płynu poruszającymi się względem siebie. Wynikiem lepkości są również stopniowe straty (dysypacja) energii mechanicznej.

Przy omawianiu dynamiki płynów ograniczymy się głównie do przepływów ustalonych, bezwirowych, nieściśliwych i nielepkich.

Przepływ laminarny cieczy:

Ruch warstwowy, czyli laminarny - nazwa ta pochodzi stąd, że wyróżnić możemy warstwy cieczy poruszające się z różnymi szybkościami. Chodzi tu zresztą o szybkości niewielkie, a grubość płynącej w ten sposób warstwy cieczy jest rzędu grubości warstwy granicznej. Przykład przepływu laminarnego stanowi ciecz płynąca przez wąską rurkę np. kapilarę. Rozkład szybkości przepływu cieczy w rurce przedstawia rysunek:

Największą szybkość przepływu posiada ciecz płynąca wzdłuż osi rurki, na ściankach szybkość ta spada do zera, gdyż ciecz przylega do ścianek. Między atomami cieczy i naczynia wytworzą się tzw. siły przylegania, które powodują, że ciecz przy ściankach nie porusza się.

Warto zwrócić uwagę na to, że przepływ laminarny cieczy przez rurkę jest przepływem wirowym.

Przepływ turbulentny cieczy:

Gdy wartość liczby Reynoldsa dla przepływu cieczy lepkiej w rurze przekracza 1160, przepływ zmienia swój charakter: z laminarnego staje się turbulentny. Tę zmianę charakteru możemy za Reynoldsem pokazać za pomocą doświadczenia pokazanego niżej:

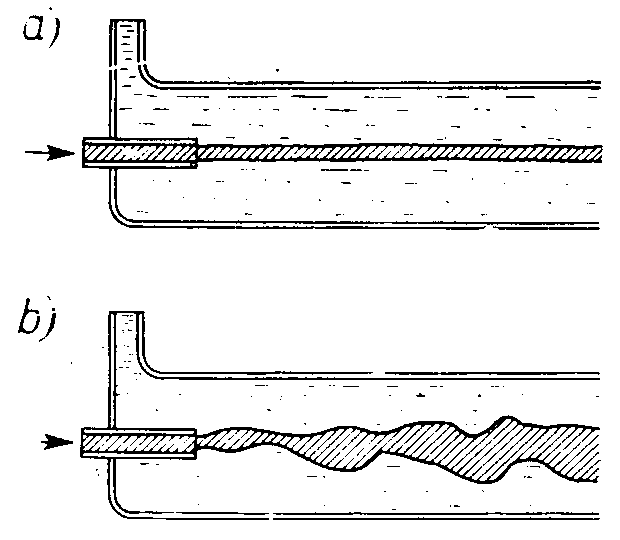
Do płynącej przez rurę cieczy wprowadzamy za pomocą dodatkowej rurki wąski strumień zabarwionej cieczy. Gdy przepływ jest laminarny, zabarwiony strumień płynie prostolinijnie, gdy zwiększymy szybkość przepływu, po przekroczeniu krytycznej wartości liczby Reynoldsa strumień zabarwionej cieczy staje się nieregularny - tworzą się zagięcia.

Rozkład szybkości przepływu cieczy wzdłuż średnicy rurki ma przy przepływie turbulentnym inny przebieg niż przy przepływie laminarnym, co przedstawia rysunek:

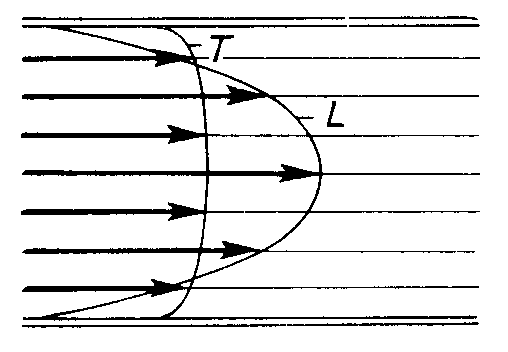
T - przepływ turbulentny ; L - przypływ laminarny.

W przepływie laminarnym występuje siła tarcia wewnętrznego, którą można zapisać:

η - współczynnik lepkości

s - pole przekroju

- pochodna prędkości

Różnica ciśnień p₁ i p₂ powoduje ruch płynu działając na cylinder o promieniu z siłą:

F = πz²(p₁ - p₂)

W przypadku gdy F_t + F = 0 wystąpi przepływ stacjonarny gdy s = 2πzl

Objętość cieczy przepływającej w czasie t przez rozważany walec wyraża się wzorem:

Podstawiając za V(z) wyżej nadmienione wyrażenie otrzymam:

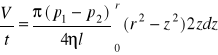
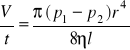
równanie Poiseuille'a

Równanie to mówi, że prędkość przepływu laminarnego przez rurke (walec) jest wprost proporcjonalny do różnicy ciśnień i czwartej potęgi promienia rurki a odwrotnie proporcjonalny do jej długości.

Prawo Poiseuille'a określa natężenie przepływu laminarnego cieczy przez wąską poziomą rurkę.

Równanie Bernoulliego:

ρ - gęstość płynu

h - wysokość słupa płynu

V - prędkość płynu

W przepływie ustalonym suma trzech ciśnień, zewnętrznego p, hydrostatycznego ρgh, hydrodynamicznego
jest dla danej strugi cieczy wielkością stałą.

W naszym doświadczeniu miarą różnicy ciśnień jest różnica poziomów Δh cieczy w rurkach.

p₁-p₂ = ρgΔh

Podstawiając do wzoru Poiseuille'a otrzymujemy:

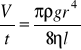
Jest to zależność liniowa o współczynniku:

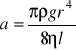
Wyznaczam promień wewnętrzny rurki:

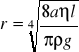
Po podstawieniu wyznaczam liczbę Reynoldsa:

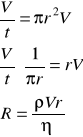
II.CZĘŚĆ PRAKTYCZNA

Wyniki otrzymane podczas przeprowadzenia doświadczenia zestawiłem w tabeli nr. 1

Tab.1

Δh[m]	Δhśr[m]	t1[s]	t2[s]	t3[s]	tśr[s]		l[m]
0,35 0,318 0,347	0,338	260,4	276,1	276,2	270,9	1,84 · 10^-7	1,10
0,319 0,34 0,293	0,317	279,4	317,9	304,1	300,46	1,66 · 10^-7	0,97
0,366 0,327 0,316	0,366	335,1	283,2	309,8	309,36	1,61 · 10^-7	1
0,196 0,32 0,278	0,264	468,1	302,1	306,8	359	1,38 · 10^-7	0,76
0,318 0,335 0,275	0,309	307,9	346,9	342,8	332,53	1,50 · 10^-7	0,90

By skorzystać z metody regresji linowej korzystam z wyników otrzymanych w tabeli nr. 2

Tab.2

xi(Δh)	yi	xi^2	yi^2	xi · yi
0,338	1,84 · 10^-7	0,114	3,39 · 10^-13	6,22 · 10^-8
0,317	1,66 · 10^-7	0,1	2,76 · 10^-13	5,15 · 10^-8
0,366	1,61 · 10^-7	0,134	2,59 · 10^-13	5,89 · 10^-8
0,264	1,38 · 10^-7	0,0697	1,90 · 10^-13	3,64 · 10^-8
0,309	1,50 · 10^-7	0,0955	2,25 · 10^-13	4,64 · 10^-8
1,594

Obliczam współczynniki a i b ze wzoru:

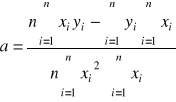
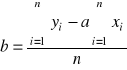
a = - 0,00175

b = 0,000558

Obliczam niepewność dla współczynnika a i b ze wzoru:

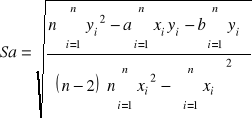
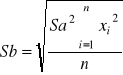
Sa = 0,00282

Sb = 0,000905

Obliczam promień wewnętrzny rurki:

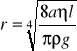
η - 1,002 · 10^-3kg/m²s

l = 1m

ρ - 100kg/m³

r = 0,45 · 10^-5

Obliczam niepewność maksymalną Δr:

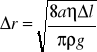
Δr = 0,670 · 10^-5

Obliczam liczbę Reynoldsa dla największej wartości Δh:

Re = 759,4

Wnioski:

Doświadczenie miało na celu wyznaczenie liczby Reynoldsa, w związku z tym iż liczba ta wyniosła 759,4 przepływ jest laminarnym. Wynikłe niepewności mogą być spowodowane niedokładnością przyrządów.

1

---