Budownictwo Rok I	WYZNACZANIE WSPÓŁCZYNNIKA ABSORPCJI PROMIENI γ	06.03.2008
Ćw. nr 11	Alicja Wisełka

1. Opis zagadnienia

Absorpcja to pochłanianie fal przez cząsteczki i atomy. Zjawisko to prowadzi do zmian poziomów energetycznych: rotacyjnych i wibracyjnych cząsteczek, przeskoku elektronów w atomach, jonizacji atomów.

Przemiana γ jest przejściem jądra od stanu wzbudzonego do stanu o niższej energii, która polega na emisji kwantu promieniowania elektromagnetycznego (fotonu), nazywanego kwantem γ dla podkreślenia jego jądrowego pochodzenia.

,(*)-stan wzbudzony jądra X

Promieniowanie γ jest promieniowaniem elektromagnetycznym o długości fali z przedziału 10^-10 ÷ 10^-15 m. Posiada dużą zdolność przenikania przez materię, a oddziaływać może z elektronami, jadrami, polem magnetycznym elektronów, jak również polem elektrycznym jąder. Wymienione oddziaływania mogą prowadzić do całkowitej absorpcji lub też do rozproszenia promieniowania γ. W praktyce trzy zjawiska odgrywają istotną rolę, a mianowicie :

• Absorpcja fotoelektryczna polegająca na całkowitym przekazaniu energii kwantu γ jednemu z elektronów powłoki elektronowej atomu i oderwaniu go od atomu.

• Rozproszenie komptonowskie, które zachodzi wówczas, gdy kwant γ zderzy się sprężyście z jednym z elektronów swobodnych względnie z elektronem związanym, o energii wiązania dużo mniejszej od energii kwantu, tak ze można go uważać za elektron swobodny. W wyniku tego procesu w miejsce pierwotnego kwantu pojawia się kwant rozproszony o mniejszej energii.

• Zjawisko tworzenia par występuje, gdy kwant γ posiada w polu elektrycznym jąder atomów absorbentu energie większą od 1,02 MeV. W wyniku tego oddziaływania powstaje para cząsteczek: elektron i pozyton.

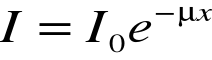
Na skutek zachodzenia wyżej wymienionych procesów oddziaływania natężenie strumienia promieni γ w miarę przechodzenia przez ośrodek maleje. Natężenie I strumienia promieniowania γ w zależności od grubości warstwy absorbenta x maleje według prawa:

=I₀ - natężenie wiązki padającej na absorbent,

I - natężenie po przejściu warstwy absorbentu o grubości x,

μ- całkowity liniowy współczynnik absorpcji (osłabienia), (zależy od materiału absorbenta, energii promieniowania γ),

Równanie to jest słuszne w warunkach dobrej geometrii, tzn. gdy wiązka promieni jest równoległa i wąska.

Inne zagadnienia związane z promieniowaniem:

• 
  Masowy współczynnik pochłaniania

• Grubość połówkowego osłabiania
  

W ćwiczeniu wykorzystany zostanie licznik Geigera - Müllera (G-M).

Przechodzące przez licznik cząsteczki wywołują wyładowania elektryczne w gazie zawartym w detektorze. Przepływające impulsy między anodą i katodą zasilacza i oporem R wytwarzają krótkie impulsy napięcia. Impulsy te są doprowadzone na siatkę lampy wzmacniacza impulsów, wzmocnione i policzone przez układ zliczający.

2. Tabela pomiarów

GRUBOŚĆ ABSORBENTA x [m]	Liczba zliczeń Nx [imp.]

III Obliczenia

1. Natężenie promieniowania gamma obliczyłam ze wzoru:

Ix = Nx/t [Ix]=imp/s

Od otrzymanej wartości należy odjąć natężenie tła. It=5 [imp/s]

Przykładowe wyniki obliczania natężenia promieniowania:

Io - wartość natężenia promieniowania żródła

Io = 57840/300 - 5 =187,8=188 [imp/s]

Pozostałe wyniki:

Lp	grubość absorbenta [m]	Ix [imp/s]	Ix-It [imp/s]
0	0	193	188
1	0,00009	142	137
2	0,00018	115	110
3	0,00027	97	92
4	0,00036	83	78
5	0,00045	72	67
6	0,00054	64	59
7	0,00063	55	50
8	0,00072	51	46
9	0,00081	45	40
10	0,0009	42	37

2. Wykres I obrazuje zależność f(x) = Ix

Za niepewność standardową przyjęłam wartość u(Ix-It) = √(Ix-It)

Niepewność standardowa natężenia źródła wynosi:

u(Io)= √Io=√188=13,7

Pozostałe wyniki:

Lp	grubość absorbenta [m]	Ix-It [imp/s]	u(Ix)=√(Ix)
0	0	188	13,7
1	0,00009	137	11,7
2	0,00018	110	10,5
3	0,00027	92	10
4	0,00036	78	8,8
5	0,00045	67	8,2
6	0,00054	59	7,7
7	0,00063	50	7,1
8	0,00072	46	6,8
9	0,00081	40	6,4
10	0,0009	37	6,0

3. Wykres II ilustruje zależność f(x)=ln(Ix)

Ix-It=(Io-It)e^-μx

Ln(Io-It)/(Ix-It)=μx

Jest to funkcja liniowa wiec wykresem zależności powinna być linia prosta jednak z przyczyny błędu pomiarów linia wykresu nie przybrała takiej postaci.

Np. Ln((Io-It)/(lnI1-It))=ln(188/137)=ln(1,37)=0,3133549=0,313

Lp	grubość absorbenta x[m]	Ix-It [imp/s]	ln(Io-It)/(Ix-It)
0	0	188	0
1	0,00009	137	0,313
2	0,00018	110	0,539
3	0,00027	92	0,72
4	0,00036	78	0,88
5	0,00045	67	1
6	0,00054	59	1,2
7	0,00063	50	1,3
8	0,00072	46	1,4
9	0,00081	40	1,5
10	0,0009	37	1,6

Korzystając z programu komputerowego Excel zastosowałam metodę regresji liniowej. Otrzymane dane:

a= 1734,32

b= 0,18

Δa= 92,42

Δb= 0,05

Prosta regresji ma postać:

y=1734,32x+0,18

(prosta ta widoczna jest na wykresie II)

Zatem:

Liniowy współczynnik pochłaniania wynosi: a= 1734,32 = μ

a jego niepewność standardowa: Δa=92,42.

Niepewność złożoną u(ln((Io-It)/(Ix-It))) określiłam z prawa przenoszenia niepewności zawartego w skrypcie:

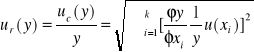
Dla funkcji f(x)=ln((Io-It)/(Ix-It)) wzór ten przyjmuje postać:

u(ln(Ix))=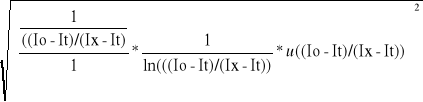

Przykładowo:

u(ln((Io-It)/(I1-It))=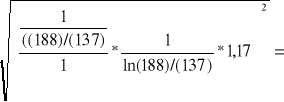
0,0272

Pozostałe wyniki:

Lp	grubość absorbenta [m]	(Io-It)/(Ix-It)	u(Io-It)/(ix-It)= √(Io-It)/(ix-It)	u(ln((Io-It)/(Ix-it)))
0	0	1	1	0
1	0,00009	1,37	1,17	0,0272
2	0,00018	1,71	1,31	0,0222
3	0,00027	2,1	1,4	0,022
4	0,00036	2,4	1,6	0,023
5	0,00045	2,8	1,7	0,024
6	0,00054	3,2	1,8	0,026
7	0,00063	3,7	1,9	0,029
8	0,00072	4,1	2,0	0,031
9	0,00081	4,6	2,2	0,035
10	0,0009	5,1	2,3	0,038

5)Grubość połówkowego osłabienia x1/2 wynosi:

x1/2=ln2/μ = 0,693147 / 1734,32= 0,000399665

IV Wyniki

Natężenie promieniowania gamma po przejściu przez absorbent o odpowiednich grubościach wynosi wg moich obliczeń:

Bez absorbenta: I=188 +-14 [imp/s]

0,00009 m : I=137+- 12 [imp/s]

0,00018 m : I=110 +- 11 [imp/s]

0,00027 m : I=92 +- 10 [imp/s]

0,00036 m : I=78 +- 9 [imp/s]

0,00045 m : I=67 +- 8 [imp/s]

0,00054 m : I=59 +- 8 [imp/s]

0,00063 m : I=50 +- 7 [imp/s]

0,00072 m : I=46 +- 7 [imp/s]

0,00081 m : I=40 +- 6 [imp/s]

0,0009 m : I=37 +- 6 [imp/s]

A liniowy współczynnik pochłaniania wynosi: μ = 1734,32

V Wnioski

W ćwiczeniu wyznaczono zależność wartości natężenia promieniowania od grubości warstwy absorbenta. Oto otrzymane wyniki natężenia od grubości absorbenta:

I₀=188 +-14 [imp/s]

I₁=137+- 12 [imp/s]

I₂=110 +- 11 [imp/s]

I₃=92 +- 10 [imp/s]

I₄=78 +- 9 [imp/s]

I₅=67 +- 8 [imp/s]

I₆=59 +- 8 [imp/s]

I₇=50 +- 7 [imp/s]

I₈=46 +- 7 [imp/s]

I₉=40 +- 6 [imp/s]

I₁₀=37 +- 6 [imp/s]

Zależność tą obrazuje wykres pierwszy. Krzywa ma charakter logarytmiczny. Wyznaczono również zależność logarytmu natężenia promieniowania od grubości warstwy absorbenta. Zależność tą przedstawia wykres drugi. Wykres ten powinien być zależnością liniową (czyli zależnością proporcjonalną), jednak nie stało się tak z powodu błędów pomiarów. Obliczono również wartość współczynnika pochłaniania μ, który jest odwrotnie proporcjonalny do grubości absorbenta.

Z przeprowadzonych pomiarów oraz obliczeń możemy wywnioskować, że wraz ze wzrostem grubości absorbenta natężenie promieniowania malało.

7

gdzie ρ - gęstość absorbenta

gdzie

x_1/2 - grubość absorbenta, dla której:

---