Budownictwo Rok I
|
WYZNACZANIE DŁUGOŚCI FALI ŚWIETLNEJ ZA POMOCĄ SIATKI DYFRAKCYJNEJ |
23.03.2008 |
Ćw. nr 12 |
Alicja Wisełka |
|
Opis teoretyczny
Fale świetlne (elektromagnetyczne) związane są z rozchodzeniem się w przestrzeni zmiennego pola elektrycznego E i magnetycznego H, przy czym wektor natężenia pola elektrycznego jest prostopadły do wektora natężenia pola magnetycznego. Kierunki drgań tych wektorów są prostopadłe do kierunku rozchodzenia się fali, tak więc fala świetlna jest falą poprzeczną.
Zjawisko dyfrakcji to ugięcie się fali, odchylenie się od prostoliniowości. Zjawisko to można wyjaśnić w oparciu o zasadę Huyghensa, głoszącą, że każdy punkt, do którego dotrze zaburzenie (fala) staje się źródłem nowej fali cząstkowej. Wypadkowe zaburzenie rozchodzące się w ośrodku jest sumą wszystkich fal cząstkowych.
Zjawisko dyfrakcji wraz ze zjawiskiem interferencji, czyli nakładania się fal, znalazło zastosowanie przy wyznaczaniu długości fali świetlnej. Najprostszym przyrządem służącym do tego celu jest siatka dyfrakcyjna, czyli szereg równomiernie rozmieszczonych szczelin wytworzonych w materiale nieprzeźroczystym. Odległość pomiędzy środkami dwu sąsiednich szczelin nazywamy stałą siatki (d).
Gdy na siatkę pada światło monochromatyczne o długości fali λ. Na ekranie otrzymamy wówczas szereg prążków, na przemian jasnych i ciemnych. Powstanie jasnych prążków wynika z interferencyjnego wzmocnienia promieni pochodzących z sąsiednich szczelin siatki.
Różnica dróg optycznych promieni pochodzących z sąsiednich szczelin wynosi:
![]()
![]()
- różnica dróg optycznych
d - stała siatki
![]()
- kąt ugięcia
Ugięcie na siatce dyfrakcyjnej:
Wzmocnienie interferencyjne w danym punkcie przestrzeni zachodzi wtedy, kiedy różnica dróg optycznych interferujących promieni jest równa całkowitej wielokrotności długości fali:
![]()
k- liczba całkowita
λ- długość fali promienia interferencyjnego
czyli: ![]()
WYKONANIE POMIARÓW:
Średnia odległość prążka od szczeliny: ![]()
Wartość sinusa kąta ugięcia α wyznaczamy z zależności trygonometrycznych. Jeżeli oznaczymy odległość miedzy siatką dyfrakcyjną a miejscem na ekranie, w którym powstał prążek l to:
![]()
Korzystając w prawa Pitagorasa otrzymamy: ![]()
b- odległość miedzy ekranem a siatka
otrzymujemy: 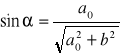
Ostatecznie otrzymujemy: 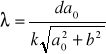
Natomiast stała siatki dyfrakcyjnej wyraża się wzorem:
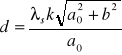
Pomiary
TABELA POMIARÓW
Rodzaj światła |
Rząd widma |
Odległość prążka od szczeliny |
Odległość ekran-siatka b [m] |
Długość fali λ [nm] |
||
|
|
Na lewo a1 [m] |
Na prawo a2 [m] |
Średnia a0 [m] |
|
|
|
|
|
|
|
|
|
III Obliczenia
1) Stała siatki dyfrakcyjnej wynosi:
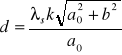
Wiedząc, że długość fali światła sodowego wynosi 588,9 nm wyliczyłam stałą siatki dyfrakcyjnej kolejno dla 3 prób a za wynik przyjęłam średnią arytmetyczną tych wyników.
Przykład obliczeń dla prążka pierwszego rzędu światła sodowego:
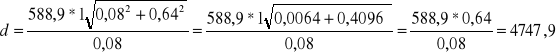
Pozostałe wyniki:
RODZAJ SWIATŁA I RZĄD WIDMA |
ODLEGŁOŚĆ PRĄŻKÓW OD SIEBIE |
ŚREDNIA ODLEGŁOŚĆ PRĄZKÓW OD ŚRODKA |
DŁUGOŚĆ FALI [nm] |
STAŁA SIATKI DYFRAKCYJNEJ |
SREDNIA STAŁA SIATKI |
Światło sodowe |
[m] |
|
|
|
|
1 |
0,16 |
0,08 |
588,9 |
4747,9 |
4819,9 |
2 |
0,32 |
0,16 |
|
4856,2 |
|
3 |
0,5 |
0,25 |
|
4855,6 |
|
Stała tej siatki dyfrakcyjnej wynosi: d=4819,9 [nm]
2)Długość fali wyraża się wzorem: 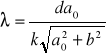
Jednostka: 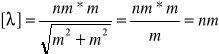
Znając już stałą siatki wyliczyłam długości fali świetlnych dla poszczególnych filtrów, następnie je uśredniłam.
Przykładowo:
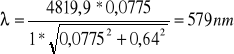
Pozostałe wyniki obrazuje poniższa tabela:
SWIATŁO MIKROSKOPOWE |
ODLEGŁOŚĆ PRĄŻKÓW OD SIEBIE |
ŚREDNIA ODLEGŁOŚĆ PRĄZKÓW OD ŚRODKA a |
DŁUGOŚĆ FALI |
SREDNIA DŁ. FALI [nm] |
POMARANCZOWE |
||||
1 |
0,155 |
0,0775 |
579 |
583 |
2 |
0,32 |
0,16 |
584 |
|
3 |
0,502 |
0,251 |
587 |
|
CZERWONE |
||||
1 |
0,175 |
0,0875 |
653 |
638 |
2 |
0,349 |
0,174 |
634 |
|
3 |
0,542 |
0,271 |
626 |
|
FIOLETOWE |
||||
1 |
0,123 |
0,0615 |
462 |
451 |
2 |
0,238 |
0,119 |
440 |
|
3 |
||||
ZIELONE |
||||
1 |
0,143 |
0,0715 |
535 |
539 |
2 |
0,297 |
0,148 |
545 |
|
3 |
0,455 |
0,228 |
538 |
|
3) Niepewność wzorcowania obliczyłam ze wzoru u(an) = an * Δdx gdzie Δdx=0,005 [m]
Np. dla światła sodowego u(a1)= 0,08* 0,005 = 0,0004 [m]
otrzymałam następujące wyniki:
RODZAJ SWIATŁA I RZĄD WIDMA |
ODLEGŁOŚĆ PRĄZKÓW |
ŚREDNIA ODLEGŁOŚĆ |
NIEPEWNOŚĆ WZORCOWANIA u(a) |
|
[m] |
||
Światło sodowe |
|||
1 |
0,16 |
0,08 |
0,0004 |
2 |
0,32 |
0,16 |
0,0008 |
3 |
0,5 |
0,25 |
0,0012 |
Światło mikroskopowe |
|||
POMARANCZOWE |
|
||
1 |
0,155 |
0,0775 |
0,000388 |
2 |
0,32 |
0,16 |
0,0008 |
3 |
0,502 |
0,251 |
0,00126 |
CZERWONE |
|
||
1 |
0,175 |
0,0875 |
0,000438 |
2 |
0,349 |
0,1745 |
0,000872 |
3 |
0,542 |
0,271 |
0,00136 |
FIOLETOWE |
|
||
1 |
0,123 |
0,0615 |
0,000308 |
2 |
0,238 |
0,119 |
0,000595 |
3 |
BRAK WIDOCZNOŚCI |
|
|
ZIELONE |
|
||
1 |
0,143 |
0,0715 |
0,000358 |
2 |
0,297 |
0,1485 |
0,000742 |
3 |
0,455 |
0,2275 |
0,00114 |
Niepewność eksperymentatora obliczyłam ze wzoru:
u(b) = b * Δex =0,64 * 0,002 = 0,0013 [m]
4) Niepewności całkowite pomiaru uc(d) i uc(λ) obliczyłam według wzoru ze skryptu:
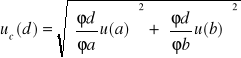
Pochodne cząstkowe wynoszą:
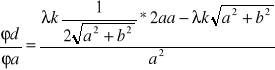
po przekształceniu: 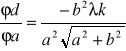
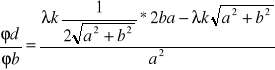
po przekształceniu: 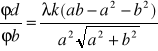
Znając wcześniej wyliczone wartości u(a) i u(b) obliczyłam niepewność pomiary uc(d):
Np. dla prążków rzędu pierwszego światła przechodzącego przez filtr pomarańczowy niepewność całkowita wynosi:
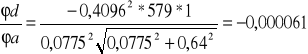
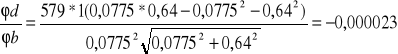
![]()
Wynik ten jest wyrażony w metrach. Wiedząc, że nm=10-9 m otrzymałam wynik: u(d)=38 nm
POM. |
niepewność wzorcowania u(a) |
(φd/φa) |
(φd/φb) |
u(d) [nm] |
1 |
0,000388 |
-0,0000618 |
-0,000023 |
38 |
2 |
0,0008 |
-0,000028352 |
-0,000010025 |
26 |
3 |
0,001255 |
-0,000016643 |
-0,000005990 |
22 |
CZER. |
||||
1 |
0,00044 |
-0,000054 |
-0,00002 |
35 |
2 |
0,00087 |
-0,000026 |
-0,000009 |
25 |
3 |
0,0014 |
-0,000015 |
-0,000006 |
22 |
FIOL. |
||||
1 |
0,00031 |
-0,000077655 |
-0,000029313 |
44 |
2 |
0,00059 |
-0,000039150 |
-0,000014079 |
29 |
3 |
||||
ZIEL. |
||||
1 |
0,00036 |
-0,000066 |
-0,000029 |
40 |
2 |
0,00074 |
-0,000031 |
-0,000011 |
27 |
3 |
0,0011 |
-0,000019 |
-0,0000067 |
23 |
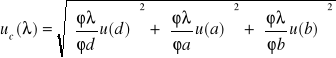
Pochodne cząstkowe wynoszą:
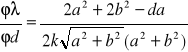
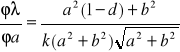
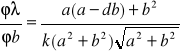
Znając wcześniej obliczoną wartość uc(λ) otrzymałam wyniki:
Dla prążków rzędu pierwszego światła przechodzącego przez filtr pomarańczowy niepewność całkowita wynosi:
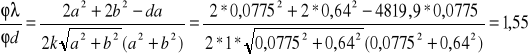
![]()
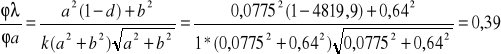
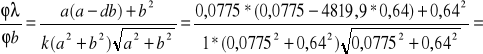
0,39
![]()
=58 [nm]
Pozostałe wyniki:
POMARANCZOWE |
φλ/φd |
φλ/φa |
φλ/φb |
u [nm] |
1 |
1,55 |
0,39 |
0,39 |
58 |
2 |
0,76 |
0,28 |
0,28 |
20 |
3 |
0,48 |
0,22 |
0,22 |
11 |
CZERWONE |
|
|
|
|
1 |
1,55 |
0,39 |
0,39 |
54 |
2 |
0,75 |
0,29 |
0,29 |
19 |
3 |
0,48 |
0,23 |
0,23 |
10 |
FIOLETOWE |
|
|
|
|
1 |
1,56 |
0,39 |
0,39 |
69 |
2 |
0,77 |
0,28 |
0,28 |
23 |
3 |
|
|
|
|
ZIELONE |
|
|
|
|
1 |
1,55 |
0,39 |
0,39 |
62 |
2 |
0,76 |
0,28 |
0,28 |
20 |
3 |
0,49 |
0,22 |
0,22 |
11 |
Z otrzymanych wyników wyliczyłam średnią arytmetyczną dla każdego rodzaju światła.
Niepewności pomiarowe wyniosły dla światła:
Pomarańczowego : 30 [nm]
Czerwonego: 28 [nm]
Fioletowego: 46 [nm]
Zielonego: 31[nm]
WYNIKI KOŃCOWE:
SWIATŁO MIKROSKOPOWE |
DŁ. FALI [nm] |
POMARANCZOWE |
|
|
583,5 +- 30 |
|
|
|
|
CZERWONE |
|
|
637,8+-28 |
|
|
|
|
FIOLETOWE |
|
|
450,8 +-46 |
|
|
|
|
ZIELONE |
|
|
539,3 +-31 |
|
|
|
|
WNIOSKI:
Celem przeprowadzonego ćwiczenia było wyznaczenie długości fali świetlnej za pomocą siatki dyfrakcyjnej. Otrzymane wyniki zgadzają się z wynikami na poszczególnych filtrach:
RODZAJ FILTRA |
MÓJ WYNIK [nm] |
WYNIK Z FILTRÓW [nm] |
POMARAŃCZOWY |
583,5 +-30 |
595+-7 |
CZERWONY |
637,8+-28 |
640+-17,2 |
FIOLETOWY |
450,8+-46 |
442+-6 |
ZIELONY |
539,3+-31 |
533+-9 |
Zanim jednak do tego doszło obliczyłam stałą siatki dla znanej długości fali światła lampy sodowej (d=4819,9 [nm]). Następnie wyznaczone zostały długości fal świetlnych dla światła z lampy mikroskopowej przepuszczonego przez filtry.
Obliczone błędy powstałe w czasie pomiarów zostały uwzględnione w przeprowadzonych obliczeniach.
4
B
A
Δ
d
α
Ekran
l
a
b
Wyszukiwarka
Podobne podstrony:
Wyznaczanie długości fali światła za pomocą siatki dyfrakcyjnej, Monika Wojakowska
Lab 24, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatk
CW 79, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatki
POPRAWA, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siat
24 Wyznaczanie długości fali światła za pomocą siatki dyfrakcyjnej i spektrometru
Ćw 85-Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
fizy2 sprawozdanie15 wersja2, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali ś
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej”, Szkoła, Fizyka
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej, Wrocław, dn. 16.11.94
Ćw 85 Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej 3 DOC
więcej podobnych podstron