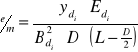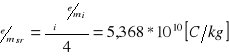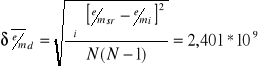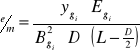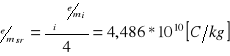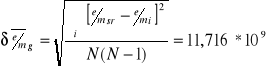POLITECHNIKA WROCŁAWSKA |
Spraw. Wyk.: Piotr BARON |
Wydział Informatyki i Zarządzania |
|||
LABORATORIUM Z FIZYKI Rok: 2 Semestr: 3 |
|||||
Data 26.10.1998 |
Temat: Wyznaczanie stosunku e/m elektronu |
Ocena: |
|||
Nr.lab. : 1. Nr.ćw. : 52. |
|
|
|||
I. CEL ĆWICZENIA.
Celem ćwiczenia jest zapoznanie się ze zjawiskiem ruchu elektronów w polu elektrycznym i magnetycznym oraz z metodami wyznaczania ładunku właściwego elektronu.
II. WSTĘP TEORETYCZNY.
II.1. Ruch elektronów w polu elektrycznym i magnetycznym.
II.1.1. Siła działająca na elektron w polu elektrycznym o natężeniu E.
F = e E
Praca sił pola elektrycznego powoduje tylko zmianę energii kinetycznej elektronów, więc z zasady zachowania energii można napisać:
![]()
![]()
- prędkość poruszającego się elektronu w polu elektrycznym
II.1.2. Siła działająca na elektron poruszający się z prędkością v, w jednorodnym polu magnetycznym.
Fm = e v B sin α
Gdy B = const., to siła Fm ma charakter siły dośrodkowej, wtedy:
r - promień toru kołowego, po którym porusza się elektron w jednorodnym polu magnetycznym.
II.2. Metoda Thomsona (poprzecznego pola magnetycznego).
Metoda Thomsona polega na odchyleniu wiązki elektronów w poprzecznym polu magnetycznym i zrównoważeniu tego odchylenia za pomocą poprzecznego pola elektrycznego. Wiązka elektronów po odchyleniu w polu magnetycznym o kąt ϕ, zostawia ślad na ekranie w odległości y od początkowego położenia.
y = (L - l/2) ϕ = (L -l/2) l/r - prawdziwe dla małych kątów
L - odległość ekranu od punktu wejścia elektronów w pole magnetyczne
l - obszar kołowy, na którym B ≠ 0.
y =
Za pomocą poprzecznego pola elektrycznego kompensujemy wychylenie y. W momencie działania obu pól zachodzi związek:
Fm = Fe
e v B = e E
v = E/B
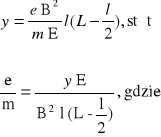
B = μo
E = U/d
II.3. Metoda podłużnego pola magnetycznego.
Na elektron poruszający się z prędkością v wzdłuż linii sił pola magnetycznego, w punkcie A działamy polem elektrycznym. Wiązka elektronów uzyskuje prędkość składową prostopadłą do linii sił pola magnetycznego , a tor ruchu ma kształt spiralny. Po wykonaniu pełnego okresu, czyli po czasie T = , elektron przetnie oś x w odległości l od punktu A
l = v T =
Wartość e/m obliczam ze wzoru:
B = μon/b I, gdzie b - długość solenoidu
n - liczba zwojów
III. OPIS PRZYRZĄDÓW POMIAROWYCH.
Miliamperomierz LM-3 (klasa dokładności 0,5)
Woltomierz LM-3 (klasa dokładności 0,5)
Woltomierz napięcia przyspieszającego LIF-04-025-1 (klasa dokładności 1,5)
IV. WYNIKI POMIARÓW I ICH BŁĘDY.
Metoda podłużnego pola magnetycznego.
IV.1. Tabela wielkości do przyjęcia w ćwiczeniu:
L.p. |
x=n/b [zw/m] |
lx [m] |
ly [m] |
μo [Vs/Am] |
Wartości |
7200±50 |
0.221 |
0.183 |
4 π * 10-7 |
Dla współrzędnych Y-kowych
L.p. |
I [A] |
U [V] |
|
Δ |
ε |
1 |
0,415 ± 0,004 |
800 ± 22,5 |
1,338*1011 |
1,355*1010 |
10,134% |
2 |
0,434 ± 0,004 |
900 ± 22,5 |
1,376*1011 |
1,394*1010 |
10,136% |
3 |
0,446 ± 0,004 |
1000 ± 22,5 |
1,447*1011 |
1,467*1010 |
10,141% |
4 |
0,468 ± 0,004 |
1100 ± 22,5 |
1,446*1011 |
1,466*1010 |
10,138% |
5 |
0,479 ± 0,004 |
1200 ± 22,5 |
1,506*1011 |
1,526*1010 |
10,137% |
6 |
0,489 ± 0,004 |
1300 ± 22,5 |
1,566*1011 |
1,586*1010 |
10,133% |
7 |
0,499 ± 0,004 |
1400 ± 22,5 |
1,619*1011 |
1,641*1010 |
10,137% |
8 |
0,511 ± 0,004 |
1500 ± 22,5 |
1,654*1011 |
1,676*1010 |
10,137% |
Dla współrzędnych X-sowych
L.p. |
I [A] |
U [V] |
|
Δ |
ε |
1 |
0,302 ± 0,004 |
800 ± 22,5 |
1,732*1011 |
1,755*1010 |
10,137% |
2 |
0,309 ± 0,004 |
900 ± 22,5 |
1,861*1011 |
1,886*1010 |
10,138% |
3 |
0,313 ± 0,004 |
1000 ± 22,5 |
2,016*1011 |
2,043*1010 |
10,134% |
4 |
0,318 ± 0,004 |
1100 ± 22,5 |
2,148*1011 |
2,177*1010 |
10,136% |
5 |
0,322 ± 0,004 |
1200 ± 22,5 |
2,461*1011 |
2,316*1010 |
9,413% |
6 |
0,328 ± 0,004 |
1300 ± 22,5 |
2,386*1011 |
2,418*1010 |
10,136% |
7 |
0,335 ± 0,004 |
1400 ± 22,5 |
2,463*1011 |
2,496*1010 |
10,137% |
8 |
0,338 ± 0,004 |
1500 ± 22,5 |
2,592*1011 |
2,628*1010 |
10,138% |
Obliczenia i wzory:
ładunek właściwy elektronu:
błąd bezwzględny ładunku właściwego:
Δ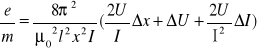
Błąd pomiarowy woltomierza:
kV=1,5 - klasa dokładności
zV=1500 [V] - zakres pomiarowy
![]()
Błąd pomiarowy amperomierza:
kA=0,5
zA=0,75 [A]
![]()
Wartość średnia ładunku właściwego
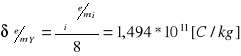
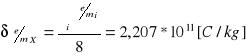
Średni błąd kwadratowy pojedynczego pomiaru
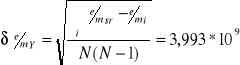
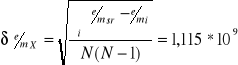
Błąd względny
![]()
Metoda Thomsona (poprzecznego pola magnetycznego).
IV.2. Tabela wielkości do przyjęcia w ćwiczeniu:
L.p. |
n |
R [m] |
d [m] |
L [m] |
D [m] |
μo [Vs/Am] |
Wartości |
650 |
0.05 ± 0.001 |
0.004 ±0.0001 |
0.09 ±0.001 |
0.100 ± 0.001 |
4 π * 10-7 |
n - ilość zwojów w cewce Helmholtza,
R - promień cewki,
d -odległość płytek odchylających,
D -średnica obszaru działania pola magnetycznego,
L - odległość ekranu od punktu wejścia elektronu w pole magnetyczne.
IV.2. Tabela wyników:
Pomiary wykonano dwa razy, przy przesunięciu plamki w górę i w dół ekranu:
Dla przesunięcia w dół:
L.p. |
y1 [m] |
I [A] |
U [V] |
B [Vs/m2] |
ΔB [Vs/m2] |
ε |
E [V/m] |
ΔE [V/m] |
|
Δ |
ε |
1 |
0,005 |
0,0115± 0,00015 |
11± 0,375 |
0,000269 |
8,88*10-6 |
3,3% |
2750 |
162,5 |
4,750*1010 |
5,944*109 |
12,5% |
2 |
0,010 |
0,0225± 0,00015 |
24± 0,375 |
0,000526 |
1,4*10-5 |
2,66% |
6000 |
243,75 |
5,421*1010 |
5,088*109 |
9,4% |
3 |
0,015 |
0,0348± 0,00015 |
38± 0,375 |
0,000814 |
1,98*10-5 |
2,43% |
9500 |
331,25 |
5,377*1010 |
4,49*109 |
8,3% |
4 |
0,020 |
0,0435± 0,00015 |
49± 0,375 |
0,001017 |
2,38*10-5 |
2,34% |
12250 |
400 |
5,922*1010 |
4,705*109 |
7,9% |
Dla przesunięcia w górę:
L.p. |
y2 [m] |
I [A] |
U [V] |
B [Vs/m2] |
ΔB [Vs/m2] |
ε |
E [V/m] |
ΔE [V/m] |
|
Δ |
ε |
1 |
0,005 |
0,0122± 0,00015 |
12± 0,375 |
0,000285 |
9,21*10-6 |
3,23% |
3000 |
168,75 |
4,617*1010 |
5,58*109 |
12,1% |
2 |
0,010 |
0,0250± 0,00015 |
24± 0,375 |
0,000584 |
1,52*10-5 |
2,60% |
6000 |
243,75 |
4,398*1010 |
4,076*109 |
9,3% |
3 |
0,015 |
0,0370± 0,00015 |
34± 0,375 |
0,000865 |
2,08*10-5 |
2,4% |
8500 |
306,25 |
4,260*1010 |
3,583*109 |
8,41% |
4 |
0,020 |
0,0475± 0,00015 |
46± 0,375 |
0,001110 |
2,57*10-5 |
2,32% |
11500 |
381,25 |
4,667*1010 |
3,708*109 |
7,9% |
Obliczenia i wzory:
Dla przesunięcia w dół: i = 1..4 - ilość pomiarów
|
dla przesunięcia w górę: i = 1..4 - ilość pomiarów
|
Rachunek błędów:
Błąd pomiarowy woltomierza:
kV=0,5 - klasa dokładności
zV=75 [V] - zakres pomiarowy
![]()
Błąd pomiarowy amperomierza:
kA=0,5
zA=0,030 [A]
![]()
Błąd bezwzględny natężenia pola elektrycznego:
![]()
Błąd bezwzględny natężenia pola magnetycznego:
![]()
Błąd bezwzględny ładunku właściwego:
![]()
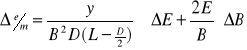
Błąd względny
![]()
V.WNIOSKI I DYSKUSJA WYNIKÓW.
Celem ćwiczenia było zapoznanie się ze zjawiskiem ruchu elektronów w polu magnetycznym i elektrycznym oraz obliczenie stosunku e/m dwoma metodami.
Metoda podłużnego pola magnetycznego wydaje mi się dokładniejsza, ze względu na mniejszą możliwość wystąpienia błędu. Plamka na ekranie była dobrze widziana i nie było problemu z jej identyfikacją. Wynik e/m wyszedł również zbliżony do rzeczywistej wartości.
Na błąd wyniku w metodzie Thomsona ma wpływ wielkość i nieostrość plamki, na ekranie lampy oscyloskopowej oraz fakt, że plamka przy zmianie natężenia pola, nie przesuwa się po lini pionowej, lecz nachylonej pod pewnym kątem. Oprócz tego na oscyloskop mogły działać pola magnetyczne urządzeń, znajdujących się w sąsiedztwie.
Na pewno na błąd w obydwu metodach mają również wpływ moje kłopoty ze wzrokiem oraz niedokładności amperomierzy i woltomierzy, są to jednak błędy małe.
- 7 -
Wyszukiwarka
Podobne podstrony:
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne, Politechnika WGGiG, Fizyka
rozne10, Politechnika WGGiG, Fizyka
rozne10, Politechnika WGGiG, Fizyka
rozne3, Politechnika WGGiG, Fizyka
rozne2, Politechnika WGGiG, Fizyka
rozne9, Politechnika WGGiG, Fizyka
więcej podobnych podstron