ru

Kiniuś™

Statystyka

Dr Elżbieta Grabowska

(notatki z wykładu 5)

29.03.2009 (niedziela)

WSKAŹNIKI ZRÓŻNICOWANIA (ROZPROSZENIA, DYSPERSJI)

DLA DANYCH ILOŚCIOWYCH

ROZSTĘP

Wstępną, orientacyjną, pozycyjną miarą zróżnicowania jest rozstęp, czyli odległość między wynikiem minimalnym a maksymalnym.

rozstęp = 150 - 195 cm

wartość rozstępu = 45 cm

Podstawową klasyczną miarą zróżnicowania danych ilościowych jest wariancja, czyli przeciętny kwadrat odchyleń od średniej.

WARIANCJA

Wariancję wyznacza się z następującego wzoru:

1) dla danych indywidualnych

2) dla danych punktowych

3) dla danych klasowych

uwaga!

Podane wzory to tzw. wariancja dla próby (wariancja estymatorem nieobciążonym)

Stosuje się również wariancję dla populacji z estymatorem

Dla populacji:

Wariancja - przyjmuje wartość minimalną = 0 gdy nie ma żadnego zróżnicowania, natomiast jej wartość maksymalna jest nieokreślona.

Wyniku wariancji nie interpretujemy, używamy go porównawczo (większa wariancja większe zróżnicowanie)

Kiniuś™

ODCHYLENIE STANDARDOWE

Bardzo wygodnym wskaźnikiem rozproszenia danych ilościowych jest odchylenie standardowe.

Jest to miara absolutna tzn. jej miano jest zgodne z mianem średniej.

S - informuje, jakie jest przeciętne odchylenie wyników w próbie od średniej.

wyniki zgodne z normą

(-1SD,+1SD)

obszar przeciętnej

zmienności

85-115 - norma dla populacji

1 prawo Czebyszewa

- W 1 SD mieści się 2/3 - ok. 68% populacji

2 prawo Czebyszewa

- W 2 SD mieści się ok. 95% populacji

3 prawo Czebyszewa

- W 3SD mieści się ok. 99,7 % populacji

! Prawie cała populacja mieści się w 3 odchyleniach standardowych.

(Odchylenie standardowe nie ma wartości 0)

Kiniuś™

WSPÓŁCZYNNIK ZMIENNOŚĆI

Dla oceny wielkości zróżnicowanie danych w próbie stosuje się pomocniczy współczynnik zmienności - v

Zasada interpretacji v:

v	zróżnicowanie
0 0,01-10% 11-33,3 % 33,4- 68 % 69-90 % 91-100 % pow.100 %	brak nikłe słabe umiarkowane silne bardzo silne ekstremalnie silne

v informuje ile procent ze średniej stanowi wielkość odchylenia standardowego, czyli jak duże jest zróżnicowanie w stosunku do średniej.

1. Przykład dla danych indywidualnych

cecha mierzona: liczba zapisanych stron na wykładzie.

l.p	xi	xi -	(x- )^2
1 2 3 4 5	2 3 3 4 6	-2,2 -0,2 -0,2 +0,8 +1,8	4,84 0,04 0,04 0,64 3,24
N=5	21	0	8,80

przeciętnie zapisano 4,2 str.

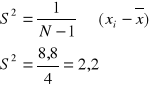
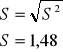
- dąży do zera

Interpretacja:

Długość notatek poszczególnych osób odchyla się przeciętnie o 1,48 kartki w górę lub w dół od średniej.

Pozwala nam to wyznaczyć obszar przeciętnej zmienności.

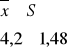
x_typ - obszar wyników najbardziej zbliżonych do średniej.

- S < x_typ <
+ S

4,20 - 1,48 4,20 + 1,48

2,72 < x_typ < 5,68

v informuje, że zróżnicowanie długości notatek mierzona odchyleniem standardowym

stanowi 35,2% ze średniej
, a więc badana grupa 5 osób jest umiarkowanie zróżnicowana ze

względu na długość notatek.

Kiniuś™

2.Przykład dla danych punktowych

cecha mierzona: liczba posiadanych płaszczy wiosennych.

0 1 2 3	10 12 7 1	0 12 14 3
	N=30	29	20,967

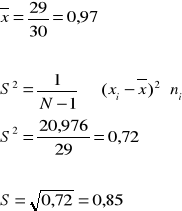
Przeciętnie na 1 osobę przypada 0,97 płaszcza.

Przeciętne odchylenie od
wynosi 0,85 płaszcza.

- S < x_typ <
+ S

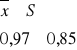
0,97 - 0,85 0,97 + 0,85

0,12 < x_typ < 1,82

( w zaokrągleniu typowe jest posiadanie od 0 do 2 płaszczy)

Grupa jest silnie zróżnicowana ze względu na ilość posiadanych płaszczy wiosennych.

3. Przykład dla danych klasowych

0-8 8-16 16-24	2 7 2	4 12 20	8 84 40
	N=11		132	256

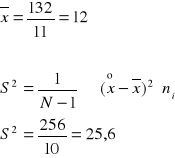
- S < x_typ <
+ S

12 - 5,06 12 + 5,06 6,94 < x_typ < 17,06

Grupa jest zróżnicowana umiarkowanie.

Kiniuś

SKOŚNOŚĆ - ASYMETRIA ROZKŁADU DANYCH

Rozkład normalny

nie ma asymetrii

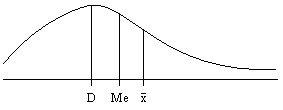
Rozkład prawostronny (dodatni)

Przewaga wyników niskich

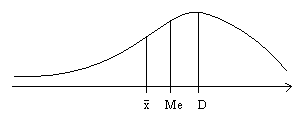
Rozkład lewostronny (ujemny)

Przewaga wyników wysokich

Najprostszym wskaźnikiem skośności jest współczynnik skośności (mieszany)

informuje o sile i kierunku skośności

(przy bardzo silnej skośności może przekraczać 1)

Zasada interpretacji:

WSK	Skośność
0 0,01-0,10 0,11-0,39 0,39-0,68 0,69-0,90 0,91-1,00 >1,00	Brak Nikła Słaba Umiarkowana Silna Bardzo silna Ekstremalnie silna

np.

W_SK = - 8,89 silna przewaga wyników niższych od średniej

(Dane z zadań z poprzednich 2 stron)

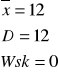
brak skośności

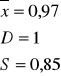
śladowa skośność ujemna

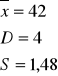
bardzo słaba skośność dodatnia

Kiniuś™

W_sk ma bardzo poważne wady:

- nie da się go wyznaczyć, gdy nie ma dominanty

- gdy dominanta jest mało wyrazista jego wynik może być dość przypadkowy

- jeżeli dla danych punktowych, dominanta jest wrażeniem skrajnym w szeregu danych to wynik W_sk może być mniej wiarygodny.

W SPSS i Exelu wyznaczana jest dokładna klasyczna miara asymetrii, czyli współczynnik A.

Współczynnik A pokazuje siłę i kierunek asymetrii

- 3 moment centralny

dane indywidualne:

dane punktowe:

dane klasowe:

Współczynnik asymetrii A - przybiera wartości: -2 < A < +2

(ale w przypadkach bardzo silnej asymetrii może przekraczać 2)

A	Asymetria
0 0,01-0,20 0,20-0,80 0,81-1,20 1,21-1,80 1,81-2,00 >2	brak nikła słaba umiarkowana dość silna bardzo silna ekstremalna

4

---