30. Cykl Carnota - obieg termodynamiczny, złożony z dwóch przemian izotermicznych i dwóch przemian adiabatycznych. Cykl Carnota jest obiegiem odwracalnym. Do realizacji cyklu potrzebny jest czynnik termodynamiczny, który może wykonywać pracę i nad którym można wykonać pracę. Cykl składa się z następujących procesów: -Sprężanie izotermiczne - czynnik roboczy styka się z chłodnicą, ma temperaturę chłodnicy i zostaje poddany procesowi sprężania w tej temperaturze (T₂). Czynnik roboczy oddaje ciepło do chłodnicy. -Sprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem, jest poddawany sprężaniu aż uzyska temperaturę źródła ciepła (T₁). -Rozprężanie izotermiczne - czynnik roboczy styka się ze źródłem ciepła, ma jego temperaturę i poddawany jest rozprężaniu izotermicznemu w temperaturze T₁, podczas tego cyklu ciepło jest pobierane ze źródła ciepła. Rozprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem i jest rozprężany aż czynnik roboczy uzyska temperaturę chłodnicy (T₂).

Dla układu tego definiuje się sprawność jako stosunek pracy wykonanej do ilości ciepła pobranego ze źródła ciepła.

Cykl Carnota jest odwracalny i może przebiegać w odwrotnym kierunku wówczas układ przekazuje energię cieplną od ciała o niższej temperaturze do ciała o wyższej temperaturze.

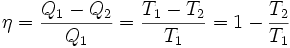
5. Pierwsza, druga i trzecia zasady Newtona: formułowanie i przykłady zastosowania.

Pierwsza zasada Newtona - Ciało pozostaje w stanie spoczynku lub w stanie stałej prędkości (0 przyśpieszenie) gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa 0)

a = 0 gdy F_wypadkowa = 0

Druga zasada Newtona - Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało

czyli F_wyp = ma

Zwróćmy uwagę, że w definicji F mówimy o pojedynczej sile, a tu mamy do czynienia z siłą wypadkową.

Trzecia zasada Newtona - gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jak ciało pierwsze działa na drugie

F_A->B = -F_B->A­

6. Druga zasada Newtona. Siła tarcia. Współczynnik tarcia statycznego i kinetycznego.

Druga zasada Newtona - Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało

czyli F_wyp = ma

Zwróćmy uwagę, że w definicji F mówimy o pojedynczej sile, a tu mamy do czynienia z siłą wypadkową.

Siła tarcia - Siły kontaktowe, o których mówiliśmy są normalne (prostopadłe) do powierzchni. Istnieje jednak składowa siły kontaktowej leżąca w płaszczyźnie powierzchni. Jeżeli ciało pchniemy wzdłuż stołu to po pewnym czasie ciało to zatrzyma się. Z drugie zasady dynamiki wiemy, że jeżeli ciało porusza się z przyspieszeniem to musi działać siła. Taką siłę nazywamy siłą tarcia.

Stosunek siły Ts do nacisku Fn nazywamy współczynnikiem tarcia statycznego µ_s. µ_s =Ts/Fn

Współczynnik tarcia kinetycznego = µ_k = Tk/Fn

7. Trzecia zasada Newtona. Siły kontaktowe.

Trzecia zasada Newtona - gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jak ciało pierwsze działa na drugie

F_A->B = -F_B->A­

Siły kontaktowe - Gdy dwa ciała są dociskane do siebie to występują między nimi siły kontaktowe. Źródłem tych sił jest odpychanie pomiędzy atomami. Przy dostatecznie małej odległości występuje przekrywanie chmur elektronowych i ich odpychanie rosnące wraz z malejącą odległością. To jest siła elektromagnetyczna i może być bardzo duża w porównaniu z siłami grawitacyjnymi.

9. Pole grawitacyjne wewnątrz kuli

Rozpatrzmy teraz pole czaszy kulistej o masie m i promieniu R. Dla r > R pole jest równe Gm/r² tj. tak jakby cała masa była skupiona w środku kuli.

Rozważmy przyczynki od dwóch leżących naprzeciwko siebie powierzchni A₁ i A₂ w punkcie P wewnątrz czaszy. Fragment A₁ czaszy jest źródłem siły F₁ ~ A₁/(r₁)² ciągnącej w lewo. Powierzchnia A₂ jest źródłem siły ciągnącej w prawo F₂ ~ A₂/(r₂)² .
Mamy więc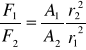
Z rozważań geometrycznych widać, że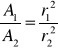
(pola powierzchni stożków ~ do kwadratu wymiarów liniowych)

Po podstawieniu do pierwszego równania otrzymujemy
Tak więc wkłady wnoszone przez A₁ i A₂ znoszą się. Można w ten sposób podzielić całą czaszę i uzyskać siłę wypadkową równą zero. Tak więc wewnątrz czaszy pole grawitacyjne jest równe zeru. Pole wewnątrz czaszy mającej skorupę dowolnej grubości też jest zero bo możemy podzielić tę skorupę na szereg cienkich warstw koncentrycznych.

Na rysunku poniżej przedstawiono pełną kulę o promieniu R i masie M.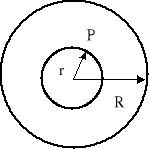
W punkcie P pole pochodzące od zewnętrznej warstwy jest zerem. Pole pochodzi więc tylko od kuli o promieniu r czyli

a = Gm/r² lub a = GρV/r²

Dla kuli V = 4πr³/3. Gęstość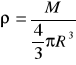
więc pole w punkcie P wynosi
Widzimy, że pole zmienia się liniowo z r.

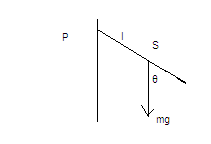
Rzut poziomy to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje się ciału prędkość początkową skierowaną poziomo.

Jak widać na rysunku, ciało wykonuje równocześnie ruch w kierunku poziomym (ciało oddala się w poziomie od miejsca wyrzucenia) oraz w kierunku pionowym (ciało opada do dołu).

Rzut poziomy jest więc złożeniem dwóch ruchów:
- w kierunku poziomym ruch ciała jest jednostajny prostoliniowy z prędkością v₀,
- w kierunku pionowym ruch jest jednostajnie przyspieszony bez prędkości początkowej - czyli swobodny spadek (w tym ruch działa na ciało siła ciężkości mg).

A. RÓWNANIE TORU RZUTU POZIOMEGO

Współrzędna x jest równa drodze przebytej ruchem jednostajnym poziomym, zatem:

Współrzędna y jest równa drodze przebytej ruchem jednostajnie przyspieszonym pionowym (swobodny spadek), zatem:

Łączymy oba wzory:

Wartości v₀ oraz g są stałe dla danego ruchu, więc weźmy sobie jakąś stałą A równą

stąd:

Wniosek:
Torem ruchu poziomego jest parabola.

B. OBLICZENIE CZASU RZUTU POZIOMEGO

Czas rzutu poziomego jest równy czasowi każdego ruchu składowego. Obliczymy go jako czas swobodnego spadku z wysokości h:

zatem:

C. OBLICZENIE ZASIĘGU RZUTU

Zasięg rzutu poziomego z jest równy drodze przebytej w kierunku poziomym ruchem jednostajnym w czasie t.

---