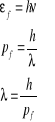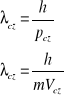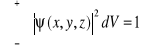Falowe właściwości cząstek

Fizyk francuski Louis de Broglie sformułował w 1924 r. hipotezę:

Jeśli światło, które traktujemy jako falę wykazuje cechy korpuskularne (ma naturę dualną) to również cząstki (np. elektrony) powinny wykazywać właściwości falowe. Zatem ruch cząstki możną opisać w języku falowym. Fale odpowiadające cząstkom są to tzw. fale materii (fale de Broglie'a).

W 1929 r. de Broglie otrzymał nagrodę Nobla.

Hipoteza fal materii

foton		cząstka
	wnioskując z analogi

Elektron przyśpieszony w polu elektrycznym przy napięciu U uzyskuje energię kinetyczna
, stad

Zatem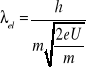
;

Jeśli U = 100 V to

Kwantowanie orbit zgodnie z hipoteza de Broglie'a

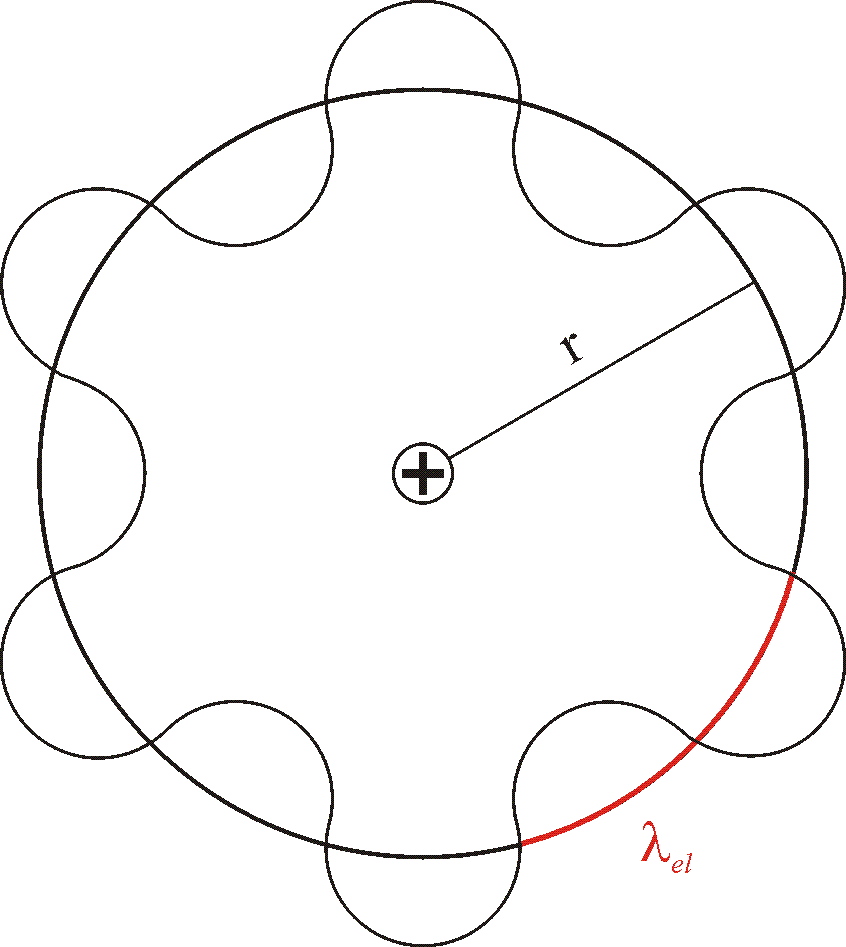
λ_el - długość fali de Broglie'a związanej z elektronem

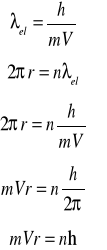
Otrzymujemy warunek kwantowy Bohra

Warunek kwantowy Bohra zawiera treść falową:

na obwodzie bohrowskiej orbity mieścić się musi całkowita liczba długości fali związanej z elektronem.

Najprostszym sposobem pogodzenia obrazu korpuskularnego z falowym jest przyjęcie interpretacji statystycznej:

natężenie fali związanej z cząstką w jakimś punkcie daje prawdopodobieństwo znalezienia cząstki w tym punkcie.

Fale de Broglie'a nazywamy falami prawdopodobieństwa.

Odpowiednikiem doświadczenia Younga byłoby, w przypadku fal materii, następujące doświadczenie.

P - w tym punkcie jest maksymalne prawdopodobieństwo dotarcia elektronu

P₂ - w tym punkcie prawdopodobieństwo dotarcia elektronu jest równe zero

Rysunek przedstawia formowanie się obrazu interferencyjnego w doświadczeniu A. Lorii. Na ekran kierował on strumień kilku elektronów na sekundę. Po dostatecznie długim czasie uwidacznia się interferencyjna struktura obrazu.

Rząd wielkości λ_el jest taki, jak długość fali promieniowania X, zatem falowe właściwości elektronów można doświadczanie zbadać tak samo, jak zbadano falową naturę promieniowania X.

Należy wiązkę elektronów skierować na kryształ. Doświadczenie taki przeprowadzili Clinton Davisson i Lester Germer (fizycy amerykańscy) i niezależnie fizyk angielski George Thomson oraz fizyk polski Szczepan Szczeniawski.

Doświadczenie Davissona-Germera (1927 r.)

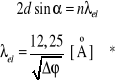
Otrzymana z równania Bragga długość fali okazała się równa długości fali obliczonej ze wzoru *.

Fala płaska de Broglie'a nie nadaje się do opisu ruchu cząstki, bo nie jest zlokalizowana przestrzennie. Taką lokalizację przestrzenną posiada paczka falowa.

E. Schrödinger wprowadził założenie, że cząstkom można przypisać fale ograniczone w przestrzeni (paczki falowe). Paczkę falową można złożyć z widma ciągłego fal, w pewnym przedziale częstości.

	Superpozycja dwóch fal harmonicznych o mało różniących się częstotliwościach (dudnienia).
	Superpozycja n fal harmonicznych Paczka falowa Prędkość grupowa ma sens fizyczny prędkości ruchu cząstki.

Erwin Schrödinger korzystając z analogii klasycznych, zapisał równanie, pozwalające znaleźć funkcję falową ψ opisującą cząstkę w określonym stanie oraz energię ε cząstki w tym stanie.

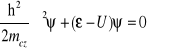
równanie Schrödingera

gdzie:

ε - energia całkowita cząstki

U - energia potencjalna

Max Born zaproponował związanie amplitudy fali de Broglie'a w każdym punkcie przestrzeni z prawdopodobieństwem znalezienia cząstki w otoczeniu tego punktu.

Prawdopodobieństwo znalezienia cząstki w elemencie objętości dV otaczającym punkt jest równe kwadratowi modułu funkcji falowej opisującej cząstkę pomnożonemu przez ten element objętości:

gdzie:

ψ - funkcja falowa ψ(x,y,z,t)

Kwadrat modułu amplitudy fali de Broglie'a w danym punkcie jest miarą prawdopodobieństwa znalezienia się cząstki w tym punkcie.

Rozumowanie prowadzące do równania Schrödingera

Równanie fali rozchodzącej się w kierunku osi x zapisujemy:

Przyjmując t jako parametr obliczmy pochodną cząstkową

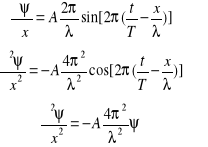
Stąd

Dla cząstki energia mechaniczna

gdzie
(ze wzoru na długość fali de Broglie'a)

Zatem:

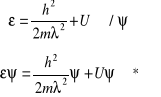
ale
. Wstawiamy do wzoru *

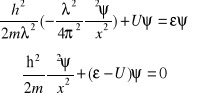
Równanie opisuje dualną naturę cząstek:

m - masa, jest atrybutem cząstki materialnej

ψ - funkcja falowa

	gęstość prawdopodobieństwa znalezienia cząstki w punkcie o współrzędnych (x,y,z)
	prawdopodobieństwo znalezienia cząstki w obszarze dV
	pewność znalezienia cząstki

Zasada nieoznaczoności Wernera Heisenberga

Zasada nieoznaczoności Heisenberga jest konsekwencją falowego opisu ruchu mikrocząstek, z wykorzystaniem pojęcia paczki falowej.

Z teorii ruchu falowego wynika, że rozciągłość Δx pewnego ciągu fal jest związana z faktem, iż musi on zawierać fale o liczbach falowych z przedziału Δk (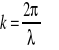
).

Wykazano, że miedzy Δx i Δk istnieje związek:

Δx * Δk ≥ 1

ale liczba falowa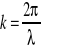
, zaś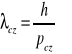
, stąd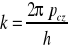
oraz ... (?)

Możemy więc zapisać:

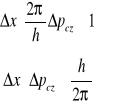
zasada nieoznaczoności

Heisenberga

Iloczyn nieoznaczoności współrzędnej położenia cząstki w kierunku danej osi (Δx) i nieoznaczoności rzutu pędu cząstki na daną oś układu współrzędnych (Δp_x) nie może być mniejszy od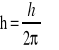
.

Przykłady:

1. Prędkość o masie 0,1 g określona jest z dokładnością

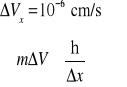
stąd można obliczyć
(niemierzalne)

Nieoznaczoność położenia elektronu w atomie w najgorszym przypadku równa rozmiarom atomu (10^-10 m). Wówczas nieoznaczoność prędkości V_x ≈ 10⁶ m/s. Tego rzędu ...

  nieoznaczoność energii

t - nieoznaczoność czasu

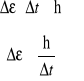
W stanie podstawowym atomu t = ∞ ;  = 0

W stanie wzbudzonym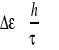
;  - czas życia w stanie zbudzonym 10^-8 s

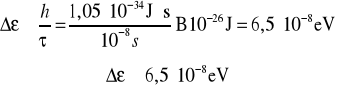
Wyemitowany kwant energii przy przejściu atomu ze stanu wzbudzonego do stanu podstawowego równa się:

Energia wypromieniowanego fotonu nie jest dokładnie równa  - ₀. Nieoznaczoność energii wynosi .

Falowe właściwości cząstek • Fizyka 2002 - 2003

8

---