RÓWNOWAGI CHEMICZNE

Obecnie przechodzimy do chyba najważniejszej części termodynamiki chemicznej czyli omówienia stanów równowagi dla reakcji chemicznych i wpływu parametrów środowiska (temperatury i ciśnienia) na położenie stanu równowagi. Jest to bardzo istotne z punktu widzenia praktycznego, gdyż pozwala przewidzieć, w jakich warunkach powinna być prowadzona reakcja, aby uzyskać jak największą wydajność w otrzymaniu produktów. Ponadto poznamy, jak można wykorzystać zbiory danych termodynamicznych do obliczania stałych równowagi, przewidywania wpływu temperatury na stan równowagi reakcji.

Rozpatrujemy układ zamknięty, znajdujący się w stałej temperaturze i pod stałym ciśnieniem, w którym zachodzi reakcja :

Kiedy przebiega reakcja chemiczna, liczby moli poszczególnych reagentów zmieniają się, ubywa substratów, przybywa produktów. Wobec tego skład układu zmienia się ciągle. Wiemy też, że entalpia swobodna zależy od składu czyli liczby moli poszczególnych składników w układzie. Ale ponieważ układ jest zamknięty czyli nie wymienia masy (materii) z otoczeniem, to zmiany liczby moli poszczególnych reagentów można ze sobą powiązać i opisać zmiany składu przy pomocy jednej zmiennej tak zwanej liczby postępu reakcji  (ksi).

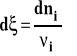
Wobec tego dla naszej przykładowej reakcji mamy :

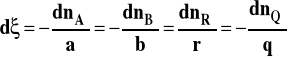
Przy substratach mamy znak minus, bo ich ilość się zmniejsza w toku reakcji. W układzie zamkniętym entalpia swobodna jest funkcją temperatury, ciśnienia i składu, który jak już wiemy, w tym wypadku można opisać jedną zmienną.

Jej różniczkę możemy zapisać następująco :

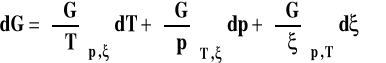
Znamy znaczenie pierwszych dwu pochodnych w tym wyrażeniu, są to minus entropia układu i objętość układu.

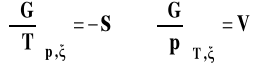
Pozostaje pytanie, czym jest pochodna entalpii swobodnej po liczbie postępu reakcji przy stałym ciśnieniu i temperaturze. Nazywamy ją entalpią swobodną reakcji.

Entalpia swobodna reakcji

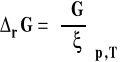
Na rysunku 1 pokazano, jak zmienia się entalpia swobodna układu w toku reakcji, gdy liczba postępu reakcji zmienia się od zera do jeden.

Rysunek 1. Zmiany entalpii swobodnej układu, w którym zachodzi reakcja chemiczna, w funkcji liczby postępu reakcji 

Widzimy, że kiedy wychodzimy od substratów, to entalpia swobodna układu maleje, osiąga minimum, a następnie rośnie. Interpretacja entalpii swobodnej reakcji na tym rysunku, to nachylenie stycznej do krzywej w danym punkcie. Początkowo, gdy entalpia swobodna układu maleje, entalpia swobodna reakcji jest ujemna, czyli reakcja przebiega samorzutnie z lewa na prawo. W minimum styczna ma nachylenie zero, czyli układ znajduje się w stanie równowagi, entalpia swobodna reakcji wynosi zero. Na prawo od minimum, entalpia swobodna układu rośnie, a więc entalpia swobodna reakcji jest dodatnia. W tym kierunku reakcja nie może dalej samorzutnie zachodzić. Na rysunku zaznaczono też standardową entalpię swobodną reakcji, która jest różnicą entalpii swobodnych czystych, rozdzielonych produktów i czystych, rozdzielonych substratów.

Jeśli wykreślimy zależność pierwszej pochodnej entalpii swobodnej układu po liczbie postępu reakcji czyli entalpii swobodnej reakcji w funkcji liczby postępu reakcji, to uzyskamy zależność pokazaną na rysunku 2.

Rysunek 2. Zależność entalpii swobodnej reakcji od liczby postępu reakcji

Reakcje egzergoniczne i endergoniczne

Kiedy liczba postępu reakcji jest mała, mniejsza od wartości dla stanu równowagi, to entalpia swobodna reakcji jest ujemna, reakcja zachodzi samorzutnie i jak wiemy, jej entalpia swobodna może być przekształcona na pracę użyteczną. Taka reakcja jest egzergoniczna. Po przekroczeniu punktu równowagi, aby reakcja przebiegała dalej z lewa na prawo, należałoby dostarczyć do układu pracę z zewnątrz, czyli jest ona niesamorzutna, wymuszona. W tym obszarze reakcja jest więc endergoniczna. W stanie równowagi reakcja nie jest ani egzergoniczna ani endergoniczna.

Pozostaje pytanie, dlaczego na krzywej opisującej zależność entalpii swobodnej układu od liczby postępu reakcji pojawia się minimum. Wyjaśnijmy to sobie na prostym przykładzie pokazanym na rysunku 3. Weźmy pod uwagę prostą reakcję w fazie gazowej, przy czym zakładamy doskonałe zachowanie układu.

Każdy z czystych reagentów ma pewną entalpię swobodną molową G_m^o. W toku reakcji zmienia się liczba moli każdego z reagentów. Jeśli na początku jest 1 mol substratu A, to w toku reakcji jego ilość maleje do zera, a produktu B rośnie od zera do jeden. W omawianym przykładzie liczba postępu reakcji jest po prostu równa ułamkowi molowemu składnika A. Gdyby entalpia swobodna układu zmieniała się tylko na skutek zmiany liczby moli składników, to można by wyrazić ją wzorem :

Jest to zależność liniowa (linia 1 na rysunku 3). Ale reagenty w toku reakcji mieszają się ze sobą cały czas i należy uwzględnić entalpię swobodna mieszania, która dla mieszaniny gazów doskonałych wyrazi się jako :

Entalpia swobodna mieszania ma zawsze wartość ujemną i w omawianym przykładzie osiąga minimum dla ułamka molowego obu składników w mieszaninie równego 0,5 (linia 2 na rysunku 3). Rzeczywista entalpia swobodna układu jest sumą obu udziałów. Linia 3 na rysunku 3 to suma zależności 1 i 2. W efekcie mamy na niej minimum wyznaczające stan równowagi reakcji.

Rysunek 3. Pochodzenie minimum na krzywej opisującej entalpię swobodną układu, w którym zachodzi reakcja chemiczna, od liczby postępu reakcji.

Jeżeli temperatura i ciśnienie są stałe, to różniczka opisują entalpię swobodną układu wyraża się następująco :

Z drugiej strony wiemy, że dla układu wieloskładnikowego możemy ją wyrazić przez potencjały chemiczne reagentów.

Zmianę liczby moli każdego z reagentów można wyrazić poprzez zmianę liczby postępu reakcji :

Ostatecznie możemy napisać :

Porównując oba wyrażenia na różniczkę entalpii swobodnej

otrzymujemy :

Otrzymany wzór jest podstawą do dalszej dyskusji równowag chemicznych.

Weźmy z powrotem pod uwagę przykładową reakcję :

Entalpię swobodną tej reakcji można wyrazić przez potencjały chemiczne następująco :

Potencjał chemiczny składnika opisany jest wzorem :

przy czym nie określamy obecnie, jak definiujemy stan standardowy i do czego odnosimy aktywność składnika. Podstawiamy wyrażenia opisujące potencjał chemiczny każdego ze składników do wzoru na entalpię swobodną reakcji :

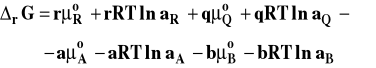
Porządkujemy to wyrażenie łącząc wyrazy zawierające logarytm razem :

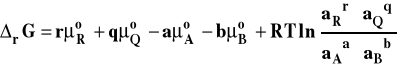
Różnica potencjałów chemicznych standardowych produktów i substratów, to nic innego jak standardowa entalpia swobodna reakcji.

Ostatecznie otrzymujemy wzór noszący nazwę izotermy van't Hoffa.

Izoterma van't Hoffa

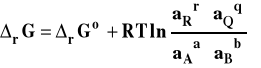
Izoterma van't Hoffa określa kierunek przebiegu reakcji chemicznej w warunkach izotermiczno-izobarycznych w zależności od aktualnego składu mieszaniny reakcyjnej. Aby z niej skorzystać, należy podstawić do wzoru wartości aktywności dla danego, aktualnego składu mieszaniny. Jeżeli _rG < 0 , to reakcja przebiera samorzutnie z lewa na prawo. Jeżeli _rG > 0 , to reakcja przebiera samorzutnie z prawa na lewo. Jeżeli _rG = 0 , to reakcja osiągnęła stan równowagi.

W stanie równowagi

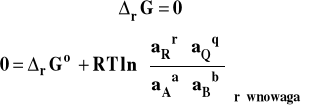
Stosunek iloczynów aktywności produktów i substratów, podniesionych do potęgi takiej, jak ich współczynnik stechiometryczny w równaniu reakcji, w stanie równowagi nazywamy stałą równowagi reakcji chemicznej.

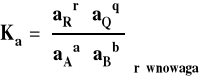
Stałą równowagi można powiązać ze standardową entalpią swobodną reakcji.

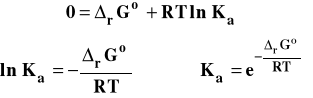
Na podstawie otrzymanego wzoru możemy wnioskować, czy stała równowagi jest mniejsza czy większa niż jeden.

Jeżeli _rG^o < 0 , to K_a > 1.

Jeżeli _rG^o > 0 , to K_a < 1.

Jeżeli _rG^o = 0 , to K_a = 1.

Ten ostatni przypadek należy traktować jako raczej teoretyczny, aczkolwiek może się zdarzyć w reakcjach wymiany izotopowej. W efekcie, jeśli na podstawie tablic termodynamicznych obliczymy standardową entalpię swobodną reakcji, to możemy na tej podstawie ocenić wielkość stałej równowagi tej reakcji.

Przejdziemy teraz do bardziej szczegółowego opisu równowag reakcji w rozmaitych przypadkach.

Reakcje w fazie gazowej, gdy gazy traktujemy jako gazy doskonałe

Weźmy jeszcze raz pod uwagę przykładową reakcję :

Entalpię swobodną tej reakcji można wyrazić przez potencjały chemiczne następująco :

Potencjał chemiczny gazu doskonałego można opisać równaniem :

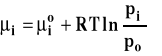
W tym wypadku stan standardowy, to stan czystego gazu pod ciśnieniem standardowym p_o, w dowolnej ustalonej temperaturze. Wartość standardowego potencjału chemicznego, przy tak wybranym stanie standardowym zależy tylko od temperatury.

Kiedy podstawimy do wzoru na entalpię swobodną reakcji wyrażenia opisujące potencjał chemiczny poszczególnych reagentów, otrzymamy :

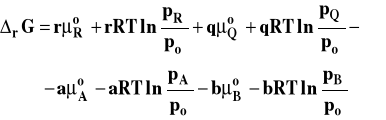
Po uporządkowaniu tego wzoru otrzymamy postać izotermy van't Hoffa dla reakcji w fazie gazowej, gdy gazy traktujemy jako doskonałe.

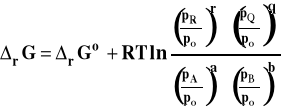
gdzie :

Ponieważ potencjały chemiczne standardowe przy przyjętym stanie standardowym zależą tylko od temperatury, to standardowa entalpia swobodna zależy też tylko od temperatury. Stałą równowagi dla reakcji w fazie gazowej, gdy gazy traktujemy jako gazy doskonałe, można zapisać następująco.

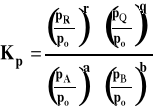
Należy pamiętać, że do wzoru podstawiamy wartości ciśnień reagentów w stanie równowagi (dla uproszczenia opuszczamy nawias i indeks oznaczający równowagę, jak to było we wzorze ogólnym). Dla podkreślenia, ze stała równowagi wyrażona jest przez ciśnienia, oznaczamy ją K_p. Należy pamiętać, że w stałej równowagi K_p, uwzględniamy tylko reagenty gazowe. Na przykład, dla reakcji :

stałą równowagi zapiszemy następująco :

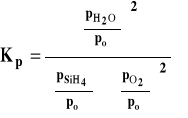
Stała równowagi K_p jest związana ze standardową entalpią swobodną reakcji wzorem :

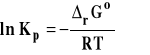
Ponieważ standardowa entalpia swobodna reakcji w tym wypadku zależy tylko od temperatury, to stała K_p zależy tylko od temperatury.

Dla reagentów gazowych możliwy jest też inny wybór stanu standardowego. Możemy jako stan standardowy wybrać stan czystego gazu pod dowolnym ciśnieniem i w dowolnej temperaturze. Wówczas potencjał chemiczny wyraża się wzorem :

Przy tak wybranym stanie standardowym potencjał chemiczny standardowy zależy od ciśnienia i temperatury. Po podstawieniu do ogólnego wzoru :

otrzymujemy

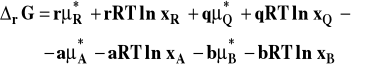
Izoterma van't Hoffa przybiera teraz postać :

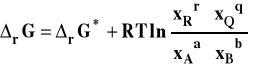
gdzie :

Stała równowagi oznaczana jako K_x, aby podkreślić, że jest wyrażona przez ułamki molowe, przybiera teraz postać :

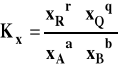
i jest związana ze standardową entalpią swobodną reakcji następująco :

Przy obecnym doborze stanu standardowego, potencjały chemiczne standardowe zależą od temperatury i ciśnienia, więc standardowa entalpia swobodna reakcji, a co za tym idzie, stała równowagi K_x zależy od temperatury i ciśnienia.

Mamy więc dwa sposoby opisania równowagi dla reakcji w fazie gazowej przez stałe równowagi K_p i K_x. Powstaje pytanie, czy są one ze sobą jakoś powiązane czy nie. Odpowiedź brzmi, tak, są powiązane. Ciśnienie cząstkowe każdego z reagentów w mieszanie równowagowej można zgodnie z prawem Daltona wyrazić jako iloczyn ułamka molowego w mieszaninie i ciśnienia całkowitego.

Po podstawieniu do wzoru na K_p, otrzymujemy :

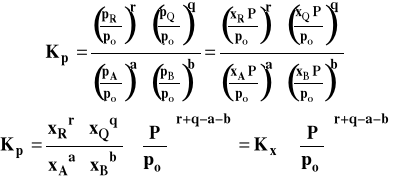
Ostatecznie związek pomiędzy K_p i K_x możemy zapisać :

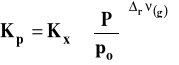
gdzie :

Należy pamiętać, że uwzględniamy w tym wzorze tylko reagenty gazowe.

Reakcje w fazie gazowej dla gazów rzeczywistych

Jak wiemy, dla gazów rzeczywistych w równaniu na potencjał chemiczny zastępujemy ciśnienie lotnością.

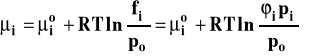
Stanem standardowym jest hipotetyczny stan gazu pod ciśnieniem standardowym w dowolnej ustalonej temperaturze, gdyby pod ciśnieniem zachowywałby się on gaz doskonały. Zastosowanie tego równania prowadzi do stałej K_p, w której ciśnienia zastąpione są lotnościami.

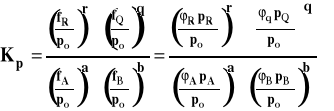
Można też stan standardowy odnieść do czystego gazu pod dowolnym stałym ciśnieniem i w dowolnej ustalonej temperaturze i potencjał chemiczny wyrazić jako :

gdzie : a_i - aktywność γ_i - współczynnik aktywności

Wówczas po zastosowaniu tego równania otrzymujemy stałą K_x.

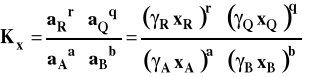
Tak jak dla gazów doskonałych, stała K_p zależy tylko od temperatury, a K_x od temperatury i ciśnienia.

Reakcje w roztworach

Reakcje przebiegające w roztworach można opisać, wyrażając stężenia jako ułamki molowe, poprzez stałą K_x. Jednak w roztworach rozcieńczonych użycie ułamków molowych jest niewygodne. Znacznie częściej korzystamy ze stężeń molarnych (lepszy wybór) lub molowych. Potencjał chemiczny składnika w roztworze doskonałym wyrażamy przy użyciu stężenia molarnego następująco :

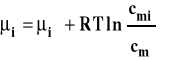
gdzie :
- potencjał chemiczny standardowy
- stężenie standardowe 1 mol/kg
- stężenie molarne substancji rozpuszczonej

Stanem standardowym jest stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/kg w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem. Potencjał chemiczny w tak dobranym stanie standardowym jest potencjałem chemicznym standardowym, którego wartość zależy od temperatury i ciśnienia. Prowadzi to stałej równowagi K_m, wyrażonej przez stężenia molarne.

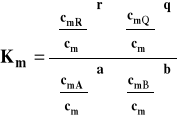
Ponieważ potencjały chemiczne standardowe zależą w tym wypadku od temperatury i ciśnienia, to stała równowagi K_m, zależy także od temperatury i ciśnienia.

Dla roztworu rzeczywistego zamiast stężenia podstawiamy aktywność, która jest funkcją stężenia roztworu, temperatury i ciśnienia.

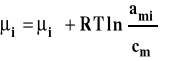
Aktywność można powiązać ze stężeniem przez współczynnik aktywności.

Stanem standardowym jest hipotetyczny stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/kg w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem, gdyby zachowywał się on jak w roztworze idealnie rozcieńczonym. Stałą równowagi można zapisać wówczas jako :

Jak wiemy, potencjał chemiczny składnika w roztworze może też być wyrażony przez stężenie molowe. W roztworze idealnym (doskonałym) równanie opisujące potencjał chemiczny wygląda następująco :

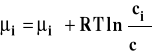
gdzie :
- potencjał chemiczny standardowy
- stężenie standardowe 1 mol/dm³
- stężenie molowe substancji rozpuszczonej

Stanem standardowym jest stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/dm³ w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem. Potencjał chemiczny w tak dobranym stanie standardowym jest potencjałem chemicznym standardowym, którego wartość zależy od temperatury i ciśnienia. Zastosowanie tego równania w ogólnym równaniu opisującym równowagę chemiczną prowadzi do stałej równowagi K_c wyrażonej przez stężenia molowe.

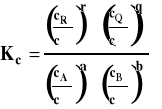
Ponieważ potencjały chemiczne standardowe w tym przypadku zależą od temperatury i ciśnienia, to stała równowagi K_c zależy od temperatury i ciśnienia.

Dla roztworu rzeczywistego zamiast stężenia podstawiamy aktywność, która jest funkcją stężenia roztworu, temperatury i ciśnienia.

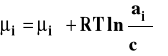
Aktywność można powiązać ze stężeniem przez współczynnik aktywności.

Stanem standardowym jest hipotetyczny stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/dm³ w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem, gdyby zachowywał się on jak w roztworze idealnie rozcieńczonym. Stałą równowagi K_c wyrazimy wówczas następująco :

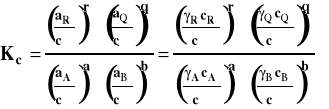
Stałe równowagi K_m i K_c stosowane są najczęściej do opisu równowag jonowych w roztworach. Należy dodać, że wszystkie stałe równowagi, niezależnie od tego czy są wyrażane przez ciśnienia czy stężenia są bezwymiarowe.

Zreasumujmy te rozważania. Ogólny wzór na stałą równowagi wyrażony jest przez aktywności reagentów.

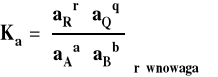
W zależności od tego, jaki układ rozpatrujemy (reakcje w fazie gazowej czy w roztworach) i czy możemy go traktować jako doskonały, czy też musimy jako rzeczywisty, co innego podstawiamy jako aktywność reagenta, i inaczej przyjmujemy stan standardowy. Czasem przyjmuje się mieszany układ odniesienia, jeśli w reakcji uczestniczą zarówno gazy jak i reagenty w roztworze. Wówczas aktywności reagentów gazowych wyrażamy przez ciśnienia, a reagentów w roztworze przez stężenia. Sposoby wyrażania aktywności i ich zastosowanie zebrano w tabeli poniżej.

Ka	stan standardowy	Aktywność	Zastosowanie
Kp	czysty składnik pod ciśnieniem standardowym 10^5 Pa w dowolnej temperaturze		gaz doskonały
Kp	czysty składnik pod ciśnieniem standardowym 10^5 Pa w dowolnej temperaturze		gaz rzeczywisty
Kx	czysty składnik pod dowolnym ciśnieniem i w dowolnej temperaturze (w odpowiednim stanie skupienia)		gaz doskonały ; roztwór doskonały
Kx	czysty składnik pod dowolnym ciśnieniem i w dowolnej temperaturze (w odpowiednim stanie skupienia)		gaz rzeczywisty; roztwór rzeczywisty
Kc	substancja rozpuszczona pod dowolnym ciśnieniem i w dowolnej temperaturze przy stężeniu standardowym c^⊗ = 1 mol/dm^3		roztwór doskonały
Kc	substancja rozpuszczona pod dowolnym ciśnieniem i w dowolnej temperaturze przy stężeniu standardowym c^⊗ = 1 mol/dm^3		roztwór rzeczywisty
Km	substancja rozpuszczona pod dowolnym ciśnieniem i w dowolnej temperaturze przy stężeniu standardowym cm^⊕ = 1 mol/kg		roztwór doskonały
Km	substancja rozpuszczona pod dowolnym ciśnieniem i w dowolnej temperaturze przy stężeniu standardowym cm^⊕ = 1 mol/kg		roztwór rzeczywisty

Wpływ temperatury i ciśnienia na stan równowagi reakcji chemicznej

W sposób jakościowy wpływ warunków (temperatury i ciśnienia) na stan równowagi reakcji chemicznej określa reguła (zasada) przekory Le Chateliera-Brauna.

Sens tej zasady jest taki, że układ poddany zmianie stara się jej sprzeciwić, stąd nazwa „reguła przekory”. Jeśli do układu będziemy dostarczać ciepło (ogrzewać go), to zareaguje on tak aby to ciepło pochłonąć. Jeśli będziemy zabierać od niego ciepło (ochładzać go), to zareaguje wydzieleniem ciepła. Jeśli zaczniemy układ sprężać (zwiększymy ciśnienie), to będzie on starał się zmniejszyć swoją objętość. Popatrzmy na dwu przykładach, jak można na podstawie reguły przekory przewidzieć wpływ temperatury i ciśnienia na stan równowagi reakcji.

PRZYKŁAD 1

Omówić wpływ temperatury i ciśnienia na stan równowagi reakcji :

reakcja egzotermiczna

Podana reakcja jest egzotermiczna, czyli wydziela się w jej toku ciepło, gdy zachodzi ona tak jak jest zapisana (z lewa na prawo). Reakcja odwrotna będzie wobec tego endotermiczna czyli w jej toku będzie pochłaniane ciepło. Jeśli będziemy podwyższać temperaturę w tym układzie (dostarczać do niego ciepło), to układ będzie starał się to ciepło pochłonąć i równowaga reakcji będzie się przesuwać w lewo (w stronę substratów), gdyż w tym kierunku reakcja jest endotermiczna. I odwrotnie, obniżanie temperatury, będzie prowadziło do przesunięcia stanu równowagi na prawo. Aby przedyskutować wpływ ciśnienia, musimy ocenić, co ma większą objętość - substraty czy produkty. W tej reakcji mamy trzy mole gazowych substratów, a tylko dwa mole gazowych produktów. W toku reakcji zmniejsza się więc objętość układu reakcyjnego. Wobec tego wzrost ciśnienia, będzie powodował przesunięcie stanu równowagi na prawo, gdyż sprężamy układ. Zmniejszanie ciśnienia będzie przesuwało stan równowagi w lewo, bo to zwiększa objętość układu.

PRZYKŁAD 2

Omówić wpływ temperatury i ciśnienia na stan równowagi reakcji :

reakcja endotermiczna

W tym wypadku, gdy układ reakcyjny będziemy ogrzewać, to dostarczone ciepło będzie pochłaniane i stan równowagi będzie przesuwał się w prawo. Czyli wzrost temperatury przesuwa w tym wypadku stan równowagi w kierunku produktów. Natomiast spadek temperatury będzie przesuwał stan równowagi w kierunku substratów, gdyż reakcja w odwrotną stronę jest egzotermiczna. Po obu stronach równania reakcji mamy taką samą liczbę moli reagentów gazowych czyli objętość układu w toku reakcji praktycznie się nie zmienia. Wobec tego ciśnienie nie będzie miało wpływu na położenie stanu równowagi w tej reakcji.

Reguła przekory, co należy podkreślić jeszcze raz, opisuje jedynie w sposób jakościowy, wpływ temperatury i ciśnienia na stan równowagi reakcji. Stan równowagi jest opisywany przez stałą równowagi, ale nie należy mylić obu tych dwu pojęć, co nagminnie czynią studenci. W sposób ilościowy opisujemy wpływ temperatury i ciśnienia na stałe równowagi. Jak wiemy, stan równowagi w zależności od wybranego stanu standardowego i stanu reagentów, może być opisany przez rozmaite stałe równowagi : K_p, K_x, K_m i K_c. Wartość stałej K_p zależy tylko od temperatury. Natomiast wartość pozostałych trzech stałych zależy od temperatury i ciśnienia.

Wpływ temperatury na stałą równowagi reakcji chemicznej - izobara van't Hoffa

Rozpatrujemy układ zamknięty, w którym zachodzi reakcja chemiczna pod stałym ciśnieniem. Skorzystamy z równania Gibbsa-Helmholtza :

Które dla wielkości standardowych dla reakcji możemy zapisać jako :

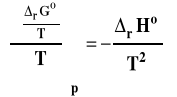
Standardowa entalpia swobodna reakcji jest związana ze stałą równowagi następującą zależnością :

We wzorze tym K_a oznacza dowolnie wyrażoną stałą równowagi czyli K_p, K_x, K_m bądź K_c. Po podstawieniu do wzoru Gibbsa-Helmholtza i zróżniczkowaniu otrzymujemy :

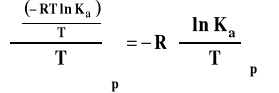
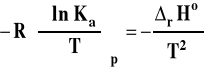
Izobara van't Hoffa

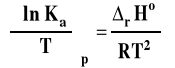
Powyższy wzór przedstawia izobarę van't Hoffa w postaci różniczkowej. Pozwala on ocenić, jaki będzie wpływ zmian temperatury na wartość stałej równowagi reakcji chemicznej.

Jeśli _rH^o < 0 (reakcja egzotermiczna), to stała równowagi K_a maleje, gdy temperatura rośnie. Spadek temperatury będzie powodował wzrost wartości stałej równowagi.

Jeśli _rH^o > 0 (reakcja endotermiczna), to stała równowagi K_a rośnie, gdy temperatura rośnie. Spadek temperatury będzie powodował spadek wartości stałej równowagi.

Aby móc obliczyć wartość stałej równowagi w jakiejś temperaturze, gdy znana jest w innej, musimy równanie izobary van't Hoffa przekształcić do postaci scałkowanej. W tym celu rozdzielamy zmienne :

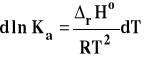
Następnie całkujemy to wyrażenie w granicach od T₁ do T₂ i odpowiednich stałych równowag w tych temperaturach.

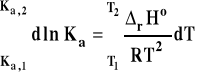
Całkowanie lewej strony jest bardzo proste.

Jeśli chodzi o prawą stronę tego równania, to sposób postępowania, będzie zależał od konkretnego zagadnienia. Jeśli zakres rozpatrywanych temperatur jest niewielki, to możemy przyjąć, że standardowa entalpia reakcji nie zależy od temperatury. Wówczas :

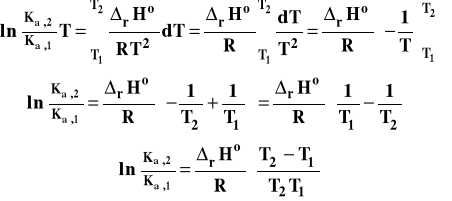
Otrzymany wzór pozwala także na obliczenie entalpii reakcji, jeśli wyznaczymy w sposób doświadczalny dwie stałe równowagi w dwu różnych temperaturach.

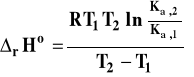
Jeśli zakres rozpatrywanych temperatur jest dość szeroki i nie można przyjąć, że entalpia reakcji jest stała, do wzoru pod całkę podstawiamy funkcję opisującą zależność entalpii reakcji od temperatury i całkujemy numerycznie. Niestety w tym w tym wypadku, nie można podać żadnego gotowego wzoru końcowego, a dla dokonania obliczeń, trzeba umieć całkować !

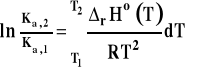
Potrzebną zależność entalpii reakcji od temperatury znajdujemy z prawa Kirchoffa, wyznaczając całkę niewłaściwą (z ruchomą górną granicą całkowania).

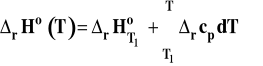
Powiedzieliśmy już, że w oparciu o scałkowaną postać izobary van't Hoffa można wyznaczyć entalpię reakcji. Poszukiwana wielkość może być obarczona dużym błędem, gdyż obliczona jest w oparciu o dwa wyniki. Jeśli są one obarczone błędem, to wynik ostateczny jest obarczony błędem i to większym niż błąd wyznaczenia samej stałej równowagi, gdyż błędy się sumują.

Aby uniknąć wpływu przypadkowych błędów na wyznaczenie entalpii reakcji, mierzy się (wyznacza doświadczalnie) stałe równowagi w kilku, kilkunastu różnych temperaturach. Następnie przekształcamy różniczkową postać izobary van't Hoffa przy założeniu, że entalpia reakcji jest stała. Będzie to oczywiści wartość średnia w badanym zakresie temperatur.

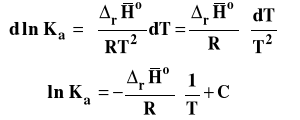
Widzimy z otrzymanej zależności, że logarytm ze stałej równowagi jest liniową funkcją odwrotności temperatury. Wobec tego współczynnik kierunkowy takiej prostej jest równy :

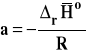
Należy wobec tego sporządzić wykres zależności lnK_a od 1/T, następnie znaleźć równanie prostej najlepiej pasującej do punktów na wykresie metodą najmniej sumy kwadratów (Excel zrobi to za nas). Współczynnik kierunkowy prostej na wykresie interpretujemy jako tangens kąta nachylenia prostej do osi argumentów. Mając wartość tego współczynnika kierunkowego, możemy obliczyć entalpię reakcji.

Ten sposób wyznaczania entalpii reakcji pokazany jest na rysunku 4. Zauważmy, że gdy reakcja jest egzotermiczna (_rH^o < 0), to na wykresie uzyskamy prostą o nachyleniu dodatnim, a gdy reakcja jest endotermiczna (_rH^o > 0), to nachylenie prostej będzie ujemne (rysunek 5).

Rysunek 4. Wyznaczanie entalpii reakcji w oparciu o izobarę van't Hoffa.

Rysunek 5. Zależność lnK od 1/T dla reakcji egzotermicznej i endotermicznej.

Wpływ ciśnienia na stałą równowagi reakcji chemicznej - izoterma van Laara-Plancka

Rozpatrujemy układ zamknięty, w którym zachodzi reakcja chemiczna, w stałej temperaturze. Z ogólnych zależności termodynamicznych wiemy, że :

co dla zmian standardowych dla reakcji możemy zapisać jako :

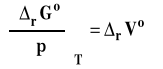
Symbol _rV^o oznacza standardową zmianę objętości w reakcji chemicznej, czyli różnicę objętości molowych w warunkach standardowych produktów i substratów, pomnożone przez odpowiednie współczynniki stechiometryczne w równaniu reakcji chemicznej.

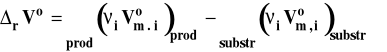
Standardowa entalpia swobodna reakcji chemicznej jest związana ze stałą równowagi następująco :

Po podstawieniu do pochodnej i przekształceniach, otrzymujemy :

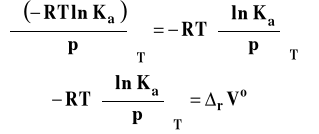
Izoterma van Laara-Plancka

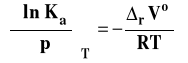
Izoterma van Laara-Plancka określa wpływ ciśnienia na stałą równowagi reakcji chemicznej w stałej temperaturze. Należy dodać, że pod ogólnie oznaczoną stałą K_a kryją się stałe K_x, K_m lub K_c, gdyż one zależą od ciśnienia. Natomiast, jak pamiętamy, stała równowagi wyrażona przez ciśnienia K_p nie zależy od ciśnienia. Ta postać stałej izotermy van Laara-Plancka pozwala wnioskować, jaki jest wpływ ciśnienia na wartość stałej równowagi.

Jeżeli _rV^o < 0 (reakcja zachodzi ze zmniejszeniem objętości czyli objętość produktów jest mniejsza niż substratów), to K_a rośnie, gdy ciśnienie rośnie.

Jeżeli _rV^o > 0 (reakcja zachodzi ze wzrostem objętości czyli gdy objętość produktów jest większa niż substratów), to K_a maleje, gdy ciśnienie rośnie.

Możemy izotermę van Laara-Plancka zapisać w postaciach szczegółowych dla K_x, K_m lub K_c.

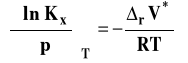
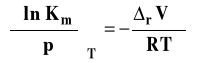
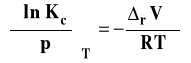
Stałą K_x stosuje się zwykle dla opisu reakcji w fazie gazowej, zaś K_m i K_c dla reakcji w roztworach. Przyjrzymy się obecnie bliżej zastosowaniu tej izotermy w różnych przypadkach.

Wpływ ciśnienia na stałą równowagi reakcji w fazie gazowej

Skorzystamy z izotermy van Laara-Plancka zapisanej dla stałej K_x.

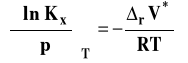
W tym wypadku standardową zmianę objętości w reakcji chemicznej możemy wyrazić następująco :

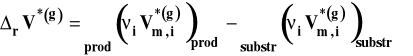
We wzorze tym uwzględniamy tylko reagenty gazowe. Zakładamy, że gazy zachowują się w sposób doskonały. W związku z tym objętość molową w stanie standardowym dla reagentów gazowych możemy wyrazić, korzystając z równania stanu gazu doskonałego jako :

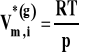
Wobec tego :

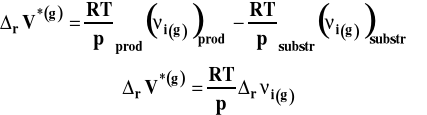
Po podstawieniu do izotermy van Laara-Plancka, otrzymujemy :

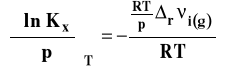
Ostatecznie izoterma van Laara-Plancka przybiera postać :

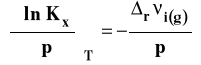
gdzie :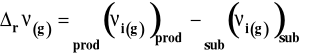

Jeżeli
(liczba moli gazowych produktów jest mniejsza niż substratów), to K_x rośnie wraz ze wzrostem ciśnienia.

Jeżeli
(liczba moli gazowych produktów jest większa niż substratów), to K_x maleje wraz ze wzrostem ciśnienia.

Jeżeli
(liczba moli gazowych produktów jest taka sama jak substratów), to ciśnienie nie ma wpływu na K_x.

Należy zauważyć, że w przypadku reakcji w fazie gazowej zmiany objętości mogą być znaczne i pływ ciśnienia na zmiany wartości stałej K_x, może być bardzo istotny.

Możemy ten wzór przekształcać dalej. Rozdzielamy zmienne i całkujemy w granicach od p₁ do p₂.

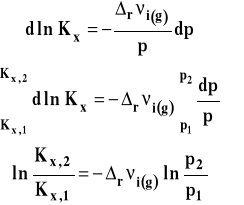
Po opuszczeniu logarytmów otrzymujemy ostatecznie:

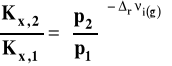
Wpływ ciśnienia na stałą równowagi reakcji w roztworach

Dla reakcji w roztworach używa się zwykle stałych K_m (lepszy wybór) lub K_c. Izoterma van Laara-Plancka, w przypadku, gdy używamy stężenia molarnego ma postać :

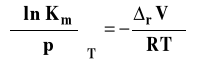
W przypadku reakcji w roztworach (a ogólniej z udziałem tylko faz skondensowanych - cieczy i ciał stałych) zmiany objętości w reakcji są rzędu cm³ (10^-6 m³), Zauważmy, że wówczas wartość ułamka po prawej stronie ma bardzo małą wartość, co powoduje, że wpływ ciśnienia na wartość stałej równowagi jest nieznaczny. Aby stała równowagi zmieniła się w zauważalny sposób ciśnienie musi się zmienić o kilka rzędów wielkości.

Możemy z dobrym przybliżeniem założyć, że zmiana objętości w reakcji jest stała i przekształcić izotermę van Laara-Plancka do postaci scałkowanej. W tym celu rozdzielamy zmienne i całkujemy w granicach od p₁ do p₂.

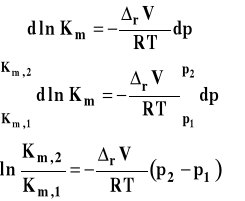
Analogicznie możemy uzyskać scałkowaną postać izotermy van Laara-Plancka dla stałej K_c.

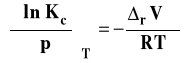
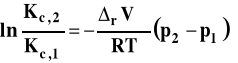
Różniczka liczby postępu reakcji to stosunek różniczkowej zmiany liczby moli danego reagenta do jego współczynnika stechiometrycznego w równaniu reakcji.

Entalpia swobodna reakcji chemicznej _rG to zmiana entalpii swobodnej układu zamkniętego o nieskończenie dużej ilości, w którym zachodzi reakcja chemiczna w warunkach izotermiczno-izobarycznych, gdy liczba postępu reakcji zmienia się o jeden, a skład układu się nie zmienia.

G

_rG>0

_rG=0

_rG<0

p,T = const

0 ξ → 1

G

stan równowagi

→

reakcja endergoniczna

reakcja egzergoniczna

T,p = const

_rG

0

1

_rG

Reakcja egzergoniczna to taka, w wyniku której uzyskujemy pracę użyteczną.

Reakcja endergoniczna to taka, która do zajścia w określonym kierunku wymaga nakładu pracy z zewnątrz.

Gdy układ znajdujący się w stanie równowagi zostanie poddany działaniu czynnika zaburzającego równowagę (bodźca), reaguje w taki sposób, aby zminimalizować zaburzenie.

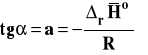
1/T

lnK

lnK

1/T





reakcja endotermiczna

reakcja egzotermiczna

---