Bryła sztywna - Zadanie 1

Treść: Cztery jednakowe kulki, każda o masie m, połączono czterema nieważkimi prętami tak, że znajdują się w wierzchołkach kwadratu o boku a. Ile wynosi moment bezwładności otrzymanego układu względem osi obrotu (przerywana linia)? Kulki traktujemy jako punkty materialne.

Dane: n = 4; m - masa każdej z kulek A, B, C i D; a - długość pręta, z którego wykonano bok kwadratu

Szukane: I = ?

Wzory:

Rysunek:

Rozwiązanie:
Rozwiązanie tego zadania polega na przekształceniu wzoru na całkowity moment bezwladności układu, a więc do dzieła :)
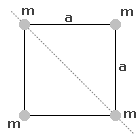
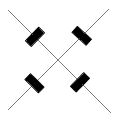
Moment bezwładności bryły to suma momentów bezwładności wszystkich punktów tej bryły, czyli dla kwadratu:

Moment bezwładności jednego punktu bryły, to iloczyn jego masy i odległości od osi obrotu.

Teraz zauważmy, że przekątna kwadratu ma długość

a odległość punktów A i C od osi obrotu to połowa długości tej przekątnej czyli:

Widzimy też, że punkty B i D leżą na osi obrotu, czyli:

Teraz wstawiamy wartości tych promieni do naszego wzoru:

A więc moment bezwładności wynosi: I=ma².

Bryła sztywna - Zadanie 2

Treść: Stosunek mas dwóch kul wynosi m1 /m2=1/2, zaś stosunek ich promieni r1 /r2=2. Jaki jest stosunek ich momentów bezwładności względem osi przechodzącej przez środki kul?

Dane: m1 /m2 = 1/2 r1 /r2 = 2

Szukane: I1 / I2 = ?

Wzory:

Szukamy stosunku I₁ /I₂.
Korzystając ze wzoru na moment bezwładności kuli:

oraz:

Liczymy stosunek i po przekształceniach otrzymujemy:

Korzystając z założeń naszego zadania otrzymujemy:

Stosunek momentów bezwładności tych kul wynosi:

Bryła sztywna - Zadanie 3

Treść: Ile wynosi praca, jaką należy wykonać, aby koło zamachowe o momencie bezwładności 1 kg^.m^2 rozpędzić tak, by wykonywało 60 obrotów w ciągu jednej minuty?

Dane: I = 1kg^.m^2 f = 60 min^-1 = 60/60 s^-1 = 1 Hz

Szukane: W = ?

Wzory:

Wiemy, że jeżeli ciało posiada pewną energię, to może wykonać pracę, która będzie równa energii tego ciała. Aby ciału "dostarczyć" energii należy więc wykonać pewną pracę, której wartość jest równa wartości energii jaką chcemy, aby to ciało posiadało.
Mówimy krótko, że praca jest równoważna energii. W naszym przypadku chcemy, żeby koło zamachowe o zadanym momencie bezwładności wykonywało określoną liczbę obrotów, czyli, żeby miało określoną energię kinetyczną ruchu obrotowego. Praca, jaką należy wykonać, aby koło zamachowe tak się zachowywało, jest liczbowo równa energii kinetycznej ruchu obrotowego naszego koła zamachowego.

A ponieważ:

więc praca jaką należy wykonać nad kołem liczbowym:

Teraz podstawimy dane

Zauważmy, że częstotliwość f wynosi 1 herc, czyli w ciągu sekundy wykonywany jest jeden obrót. Na koniec sprawdźmy jeszcze jednostkę:

Praca jaką należy wykonać wynosi: W = 20 J

Bryła sztywna - Zadanie 4

Treść: Ile wynosi moment bezwładności cienkiej, jednorodnej obręczy o masie m i promieniu r względem osi prostopadłej do płaszczyzny wyznaczonej przez obręcz i przechodzącej przez punkt P leżący na obręczy (przerywana linia na rysunku)?

Dane: m - masa obręczy r - promień obręczy

Szukane: I=?

Wzory:

Rozwiązanie:
Rozwiązanie tego zadania ogranicza się do skorzystania z twierdzenia Steinera. Oznaczmy długość odcinka OP przez a, aby można było z tego twierdzenia skorzystać.
Zauważmy ponadto, że a=r. No to do dzieła :)

(DLA DOCIEKLIWYCH)
Wyprowadzimy więc sobie wzór na I₀.
Wiemy, że moment bezwładności dowolnej bryły to suma momentów bezwładności wszystkich punktów wchodzących w skład bryły względem danej osi obrotu, co ilustruje wzór

Mamy mały problem, ponieważ obręcz składa się z nieskończenie wielu punktów.
Dokonamy tego poprzez całkowanie. Podzielmy (w ramach eksperymentu myślowego) obręcz na na nieskończenie małe elementy o długości dx. Oznaczmy elementy bezwładności każdego z tych elementów przez dI. Wprowadźmy sobie gęstość liniową jako stosunek masy do długości. W naszym przypadku

Gdzie λ to właśnie gęstość liniowa.
Element dx naszej obręczy możemy traktować jako punkt, a więc jego moment bezwładności wyraża wzór:

Przez m_dx oznaczyłem masę tego elementu tarczy.
Ale zauważmy, że

Więc nasze równanie przyjmuje postać

Teraz obustronnie scałkujemy to równanie i trochę przekształcimy

A więc słusznie zastosowaliśmy taki, a nie inny wzór na moment bezwładności obręczy :)

Szukany moment bezwładności wynosi I=2mr².

Bryła sztywna - Zadanie 5

Treść: Z jednorodnego krążka 1 o masie M i promieniu R wycięto krążek 2 o promieniu r=R/2, którego środek znajdował się w odległości r od środka krążka 1 (styczny wewnętrznie). Krążek 2 doklejono do krążka 1, tak że otwór po wycięciu i doklejony krążek są symetryczne względem środka krążka 1. Ile wynosi moment bezwładności otrzymanego układu względem osi prostopadłej do jego powierzchni i przechodzącej przez środek krążka 1?

Dane: R r = R/2 a = r Z - oś obrotu M - masa tarczy 1 m - masa tarczy 2

Szukane: I = ?

Wzory:

Rysunek:

Rozwiązanie:
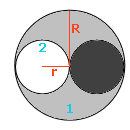
Na początku zauważmy, że tarcza 2 względem osi obrotu Z posiada moment bezwładności, który, zarówno przed jego wycięciem, jak i po wycięciu i przestawieniu, jest taki sam i równy:

a to odległość osi obrotu Z od osi związanej ze środkiem masy, a ponieważ tarcza jest jednorodna, przeto a = r.
Zauważmy, że moment tarczy 1 po wycięciu tarczy 2 i przed jej ponownym przyłożeniem jest równy:

Natomiast po przyłożeniu tarczy 2 po przeciwnej stronie osi obrotu moment bezwładności naszego układy będzie równy:

Z przedstawionych obliczeń wynika, że moment bezwładności tak skonstruowanego krążka jest taki sam, jak moment bezwładności całego krążka 1 i wynosi 0.5MR².

Bryła sztywna - Zadanie 6

Treść: Energia kinetyczna ciała obracającego się ruchem jednostajnie przyspieszonym wzrosła czterokrotnie. Jak zmieniło się w tym czasie przyspieszenie kątowe?

Dane: E = 4 E0

Szukane: Δε=?

Wzory:

Rozwiązanie:
W zadaniu mamy dwa stany - jeden początkowy (oznaczać będziemy go indeksem "0") i końcowy (bez indeksu).
Z zadania wiemy, że:

Zamieniamy więc energię kinetyczną zgodnie ze wzorem 1) - oczywiście moment bezwładności I jest bez zmian, ponieważ rozpatrujemy to samo ciało:

Przez ω rozumiemy prędkość kątową po czasie t (czyli po wzroście energii). Jest ona równa

czyli prędkości kątowej początkowej plus przyrostowi prędkości kątowej po czasie t.
Porównując dwa powyższe wzory:

A ponieważ:

to

Zatem przyspieszenie kątowe się nie zmienia, co jest oczywiste dla ruchu jednostajnie przyspieszonego, w którym zmianie ulega prędkość kątowa w czasie t.

Bryła sztywna - Zadanie 7

Treść: Punkt materialny o masie m=1kg obiega okrąg o promieniu r=1m ruchem jednostajnym z prędkością kątową ω= 2s^-1. Ile wynosi moment siły dośrodkowej względem środka okręgu?

Dane: m = 1 kg r = 1 m ω = 2 s^-1

Szukane: M = ?

Wzory:

Rozwiązanie:
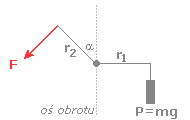
Przypomnijmy sobie najpierw, że w ruchu jednostajnym po okręgu jedyną działającą siłą jest siła dośrodkowa skierowana - jak sama nazwa mówi - do środka okręgu.
Naszym zadaniem jest policzenie wartości momentu siły dośrodkowej względem środka okręgu, który jest środkiem obrotu. Wiemy, że moment siły wyraża się wzorem:

czyli skalarnie:

Ostatni element powyższego wzoru to sinus kąta zawartego pomiędzy wektorem siły a wektorem odległości (promienia).
Pamiętajmy, że wektor siły dośrodkowej jest równoległy do wektora promienia wodzącego, więc:

Widzimy więc, że szukany moment siły dośrodkowej jest równy 0 Nm.

Bryła sztywna - Zadanie 8

Treść: Walec o masie m i promieniu r wiruje wokół osi O pod wpływem siły F. Ile wynosi przyspieszenie kątowe walca?

Dane: m r F α = 1/2 π

Szukane: ε = ?

Wzory:

Rozwiązanie:
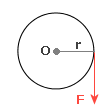
Na początek wyjaśnię dlaczego:

Otóż siła jest styczna do pobocznicy walca (prostopadła do promienia), a α to kąt między promieniem walca r a siłą F.
Siła ta ma niezerowy moment względem osi obrotu walca, który z łatwością można wyznaczyć korzystając z definicji

Ponieważ moment siły ma niezerową wartość, więc mamy do czynienia z ruchem jednostajnie przyspieszonym. Skorzystajmy z II zasady dynamiki Newtona dla ruchu obrotowego:

Na koniec wyprowadzimy jednostkę

Bryła sztywna - Zadanie 9

Treść: Jaką wartość musi przyjąć siła F, aby układ pokazany na rysunku pozostał w równowadze? Przyjąć: r1=0.4m, r2=0.5m, m=10kg, α=30 ^o.

Dane: r1 = 0.4 m r2 = 0.5 m m = 10 kg g = 10 m/s^2 α = 30 ^o

Szukane: F = ?

Wzory:

Rysunek:

Rozwiązanie:
Aby układ pozostawał w spoczynku, to suma momentów wszystkich sił musi być równa 0. Tak więc sprawdźmy dla jakiej wartości siły F tak będzie. W tym celu policzymy sumę momentów siły F i P, przyrównamy do 0 i trochę przekształcimy.

Z zapisu wektorowego wynika, że należy przyrównać wartości wektorów momentów obu sił. Kierunki i zwroty wektorów nas nie interesują (dlatego zapominamy o znaku minus).

Na koniec zwymiarujemy jeszcze ostatnie równanie

Siła ma wartość 80 N.

Bryła sztywna - Zadanie 10

Treść: Koło zamachowe w kształcie pierścienia o promieniu r=0.3m i masie m=50kg obraca się z częstością n=20s^-1. Ile musi wynosić moment siły hamującej, aby koło zatrzymało się w czasie t=20s?

Dane: m = 50 kg r = 0.3 m n = 20 Hz t = 20 s

Szukane: M = ?

Wzory:

Rozwiązanie:
Rozwiązanie tego zadania opiera się w 100% na skorzystaniu z II zasady dynamiki Newtona dla ruchu obrotowego i przepisaniu jej matematycznej formuły z uwzględnienie odpowiednich zależności. A więc do dzieła.
Wspomniana zasada ma następującą postać:

Uwzględniając, że:

oraz

i

możemy to równanie przepisać w następujący sposób:

Ponieważ my chcemy, aby koło zamachowe się zatrzymało, więc jego końcowa prędkość kątowa ω_k=0.Przekształćmy dalej nasze równanie

Minus w ostatnim równaniu oznacza, że wektory prędkości kątowej i momentu siły hamującej mają przeciwne zwroty. Ponieważ mamy policzyć wartość momentu siły, przeto pominiemy w dalszych obliczeniach ten znak, pamiętając jednak co on oznacza. Teraz wystarczy tylko zwymiarować nasze równanie i podstawić wartości liczbowe.

Na koniec sprawdzimy poprawność jednostki:

Moment siły hamującej jest równy M = 28 Nm

Bryła sztywna - Zadanie 11

Treść: Walec o masie m, promieniu r i momencie bezwładności (1/2)mr^2 stacza się bez poślizgu z równi pochyłej o wysokości h. Jaką prędkość osiągnie ten walec u podstawy równi?

Dane: m - masa walca; r - promień walca; h - wysokość równi

Szukane: v = ?

Wzory:

Rysunek:

Rozwiązanie:
Aby policzyć prędkość walca przy podstawie równi pochyłej skorzystamy z najważniejszego prawa w mechanice, czyli zasady zachowania energii. Na szczycie równi prędkość jest zerowa, czyli energia kinetyczna tez jest równa 0, natomiast energia potencjalna jest wtedy maksymalna, ponieważ przyjmujemy, że przy podstawie równi jest równa 0 (założenie to nie jest konieczne, ale ułatwi nam zapis).
Pamiętajmy również, że walec się toczy, tak więc musimy uwzględnić energię kinetyczną ruchu obrotowego (ale tylko u podstawy równi, ponieważ na jej szczycie walec się nie toczy).
Ponieważ całkowita energia mechaniczna ma się nie zmieniać podczas staczania się walca, więc energia potencjalna całkowicie przekształci się w energię kinetyczną ruchu obrotowego i postępowego. Zasada zachowania energii przyjmuje postać:

Wielkości z indeksem 1 to wartości na górze równi, a z indeksem 2 u jej podstawy.
Uwzględniając nasze założenia co do wartości energii w tych miejscach możemy napisać:

Teraz wykorzystując zależność między prędkością kątową i liniową możemy przepisać nasze równanie w następujący sposób:

Bryła sztywna - Zadanie 12

Treść: Jak zmieni się energia kinetyczna układu pokazanego na rysunku, jeżeli zwiększymy w nim dwukrotnie odległość mas od osi obrotu i równocześnie zwiększymy dwa razy prędkość kątową?

Dane: r2 = 2r1 ω2 = 2ω1 n = 4 (liczba mas)

Szukane: Ek2 / Ek1

Wzory:

Rysunek:

Rozwiązanie:
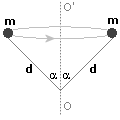
Mamy policzyć jak zmieniła energia kinetyczna po zwiększeniu odległości i prędkości kątowej. W tym celu policzymy stosunek energii w stanie drugim (po modyfikacjach układu) do energii kinetycznej w stanie pierwszym (przed modyfikacjami).
Najpierw należy zauważyć, że nasz układ wykonuje tylko ruch obrotowy, a więc całkowita energia kinetyczna to po prostu energia kinetyczna ruchu obrotowego. Ciężarki w naszym układzie możemy traktować jako punkty materialne. Energia w takim przypadku będzie równa:

Ponieważ są to identyczne ciężarki i są one równoodległe od środka obrotu, przeto nasze równanie można przepisać w następującej postaci:

Teraz wykorzystując dane zapiszemy energię w obu stanach

i policzymy ich stosunek:

Widzimy, że energia kinetyczna wzrosła 16-krotnie.

Bryła sztywna - Zadanie 13

Treść: Bryła sztywna wiruje wokół stałej osi i względem tej osi ma moment pędu L oraz moment bezwładności I. Ile wynosi okres obrotu bryły względem tej osi?

Dane: I L

Szukane: T = ?

Wzory:

Rozwiązanie:
Pamiętajmy, że okres to czas pełnego obrotu, czyli możemy napisać:

Ponieważ w zadaniu mamy dany moment pędu, musimy skorzystać również ze wzoru nr 3), który jest zapisany w postaci wektorowej. Ponieważ szukamy sposobu na wyrażenie wartości okresu, zamieniamy wzór z postaci wektorowej na postać skalarną:

gdzie sinα to kąt między wektorami pędu p i odległości (promienia) r.
Teraz zauważmy, że wektory pędu i promienia w ruchu obrotowym są prostopadłe, a więc sinα=1. Możemy więc napisać:

(tak naprawdę wystarczy, że zapamiętasz, że moment pędu w ruchu obrotowym to iloczyn masy, prędkości i odległości).

Teraz uwzględniając zależność między prędkością liniową i kątową możemy powyższe równanie przepisać w następujący sposób:

Ze wzoru na moment bezwładności wyznaczymy kwadrat promienia

Teraz powyższy wzór i wzór nr 1) wstawimy do przekształconego wzoru na moment pędu

Tak więc okres wyrażamy wzorem T=(2πI)/L.

Bryła sztywna - Zadanie 14

Treść: Ile wynosi energia kinetyczna cienkościennej rurki o masie 4g toczącej się bez poślizgu po poziomej powierzchni z prędkością 2cm/s? Jaki jest stosunek energii kinetycznej ruchu postępowego Ep do energii kinetycznej ruchu obrotowego Eo dla tej rurki?

Dane: m =4g = 0.004kg v = 2cm/s = 0.02m/s

Szukane: Ek = ? Ep / Eo = ?

Wzory:

Rozwiązanie:
Najpierw policzymy prędkość kątową tej rurki

Teraz policzymy energie kinetyczne ruchu postępowego i obrotowego, wykorzystując powyższe

Całkowita energia kinetyczna to oczywiście suma powyższych energii:

Teraz policzymy szukany stosunek. Nietrudno zauważyć, że wynosi on 1, ale dla formalności pokażemy dlaczego.

Na koniec policzymy wartość energii kinetycznej

Bryła sztywna - Zadanie 15

Treść: Moment bezwładności łyżwiarza w początkowej fazie piruetu wynosił I0. Zaniedbując opory ruchu moment bezwładności został zmniejszony czterokrotnie. Jak zmieniła się energia kinetyczna łyżwiarza?

Dane: I0 I1 = 0.25 I0

Szukane: Ek1 / Ek0=?

Wzory:

Rozwiązanie:
Moment pędu łyżwiarza nie zmienia się, ponieważ nie działają na niego żadne siły o niezerowych momentach względem osi obrotu. Przekształćmy wzór na moment siły, aby zobaczyć jak prędkość kątowa zależy od momentu bezwładności. W tym celu wykorzystamy zależność między prędkością liniową i kątową oraz stałość momentu pędu w czasie.

Widzimy z tej zależności, że jeżeli moment bezwładności zmaleje 4-krotnie, to prędkość kątowa musi zwiększyć się 4-krotnie, aby spełniona została zasada zachowania momentu pędu. Policzmy teraz energię kinetyczną tego łyżwiarza z uwzględnieniem tej zależności

Nie wolno nam ani na chwilę zapomnieć, że L=const. Teraz możemy policzyć energię kinetyczną w obu przypadkach, które nas interesują

No to teraz możemy policzyć jak się zmieniła energia kinetyczna naszego łyżwiarza

Energia kinetyczna łyżwiarza wzrosła czterokrotnie.

Bryła sztywna - Zadanie 16

Treść: Dwie kulki o masie 0.1kg każda obracają się wokół osi OO? (rysunek). Ile wynosi moment bezwładności układu kulek (kulki należy traktować jako masy punktowe), jeżeli α=30^o, d=10cm. Ile wynosi energia kinetyczna układu kulek, jeżeli wykonują one pół obrotu na sekundę?

Dane: m = 0.1 kg α = 30^o d = 10cm = 0.1m n = 2 f = 1/2 Hz φ = π

Szukane: I = ? Ek = ?

Wzory:

Rozwiązanie:
Na samym początku wyznaczymy promień wodzący tych kulek (czyli najmniejszą odległość kulek od osi obrotu OO') w ruchu po okręgu

Skoro mamy promień to nic nie stoi na przeszkodzie, abyśmy policzyli moment bezwładności kulek

Jest to jednak moment bezwładności jednej kulki. Dla naszego układu całkowity moment bezwładności będzie wyrażał się wzorem

Wartości liczbowe policzymy na samym końcu a teraz zajmiemy się energią. Na początek należy zauważyć, że nasze kulki poruszają się po okręgu ze stałą prędkością liniową, natomiast nie wykonują obrotu. Wystąpi tu prędkość kątowa, ale związana z ich ruchem po okręgu. Możemy ją łatwo policzyć, bo wiemy, że wykonują one pół obrotu na sekundę (czyli zakreślają kąt π). Więc ją policzmy

:

Teraz wyznaczymy prędkość liniową kulek w ruchu po okręgu

Ponieważ, jak już zauważyliśmy, kulki wykonują tylko ruch postępowy, więc energia kinetyczna to po prostu energia kinetyczna ruchu postępowego. Policzmy ją:

A dla obu kulek:

Sprawdzimy jeszcze, czy w ostatnim wzorze zgadzają się jednostki

HURA :)
Teraz policzymy wartości liczbowe:

Zatem szukany moment bezwładności oraz energia kinetyczna wynoszą odpowiednio:

Bryła sztywna - Zadanie 17

Treść: Jaką pracę należy wykonać, aby zwiększyć z f1 do f2 częstotliwość obrotów bryły sztywnej o momencie bezwładności I?

Dane: f1 f2 I

Szukane: W = ?

Wzory:

Rozwiązanie:
Najpierw wyznaczymy energię kinetyczną w zależności od wielkości jakie możemy wykorzystać:

Teraz możemy policzyć energię w obu stanach:

Teraz zauważyć należy, że praca jaką należy wykonać, aby zwiększyć częstotliwość obrotu naszej bryły sztywnej, to po prostu przyrost energii kinetycznej, jakiego dana bryła dozna w wyniku zwiększenia częstotliwości jej obrotu. Praca ta wyraża się wzorem, który teraz wyznaczymy.

Szukana praca wynosi W = 2π²I(f₂²-f₁²).

Bryła sztywna - Zadanie 18

Treść: Oblicz moment bezwładności układu dwóch ciał o masach 2m i m oddalonych od siebie o l, względem osi prostopadłej do linii łączącej ciała i przechodzącej przez środek masy układu. Rozmiary ciał są znikomo małe w porównaniu z l.

Dane: m1 = 2m m2 = m l M = 3m n = 2

Szukane: I = ?

Wzory:

Rysunek:

Rozwiązanie:
Na początku objaśnię używane symbole:
M - masa układu dwóch kulek;
x_i - współrzędna położenia i-tego elementu układu.
Teraz przydałoby się znaleźć środek obrotu, który pokrywa się ze środkiem masy tego układu. Oś X została tak wybrana i wyskalowana, aby policzenie środka ciężkości jak najbardziej sobie ułatwić.

Mamy więc środek masy (a więc obrotu). Nietrudno więc zauważyć, że:

Teraz skorzystamy z faktu, że rozmiary ciał są znikomo małe w porównaniu z l. Możemy je więc traktować jako punkty materialne przy liczeniu momentu bezwładności, co nie powinno już nam sprawić problemu.

Analogiczny wzór można napisać dla drugiego ciała:

Teraz już możemy policzyć całkowity moment bezwładności tego układu.

Szukany moment bezwładności wynosi I = 2/3 ml².

Bryła sztywna - Zadanie 19

Treść: W górę równi pochyłej o kącie nachylenia α=30^o wtacza się bez poślizgu kula, która u podstawy ma szybkość v0=10m/s. Oblicz drogę, jaką przebędzie wzdłuż równi do chwili zatrzymania się.

Dane: α = 30^o v0 = 10 m/s

Szukane: s = ?

Wzory:

Rysunek:

Rozwiązanie:
Aby rozwiązać to zadanie posłużymy się zasadą zachowania energii. W naszym przypadku przyjmie ona następującą postać:

Przyjmijmy, że u podstawy równi energia potencjalna jest równa 0. Założenie to nie wpływa na wynik, ale uprości troche zapis. W tym samym momencie energia kinetyczna jest największa. Gdy kula się zatrzyma (na wysokości h) jego energia kinetyczna zmaleje do zera, a energia potencjalna osiągnie swoje maksimum. Uwzględniając te założenia możemy zasadę zachowania energii dalej przekształcać. Skorzystamy także z zależności między prędkością liniową i kątową oraz ze wzoru na moment bezwładności kuli (każdy chyba zauważy moment, w którym to zastosuję :) ).

Zauważmy ponadto, że h/s=sinα. Możemy więc teraz policzyć drogę jaką przebędzie kula korzystając z wyniku poprzedniego przekształcenia i tej oczywistej zależności.

A teraz coś co wszyscy lubią, czyli sprawdzenie jednostek (czasami to pomaga wykryć jakiś błąd :)).

A na koniec policzymy wartość przebytej przez kulę drogi.

Szukana droga wynosi s = 14.27 m.

Bryła sztywna - Zadanie 20

Treść: Zawieszony pionowo jednym końcem pręt o długości l odchylamy od pionu o kąt α, a następnie puszczamy. Oblicz, jaką prędkość będzie miał koniec pręta w chwili przechodzenia przez linię pionu.

Dane: l φ0 = π/2 α

Szukane: v = ?

Wzory:

Rysunek:

Rozwiązanie:
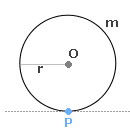
Najpierw zauważmy, że taki pręt stanowi wahadło fizyczne. Wykonuje on ruch harmoniczny prosty. Okres w tym ruchu dla naszego pręta jest równy:

Ponieważ prędkość (wartość) w ruchu harmonicznym wyraża się wzorem:

musimy skorzystać ze związku między okresem i częstością kołową i ją wyznaczyć.

Teraz zauważmy, że gdy pręt przechodzi przez pion to jego prędkość jest maksymalna. Z drugiej strony, ze wzoru na wartość prędkości widzimy, że jest ona maksymalna, gdy funkcja sinus jest równa 1. Wykorzystajmy więc ten fakt.

Teraz musimy wyznaczyć amplitudę. W tym celu posłużymy się rysunkiem. Łatwo zauważyć, że:

Mam nadzieję, że wszyscy zauważyli co zostało zrobione z sinusem (jeżeli nie to zobaczcie na wzór na sinus połowy kąta).
Teraz należy policzoną amplitudę wstawić do wcześniejszego równania wiążącego właśnie amplitudę, częstość kołową i prędkość, której szukamy.

Na koniec sprawdzimy jednostki.

Szukana prędkość wynosi

35

---