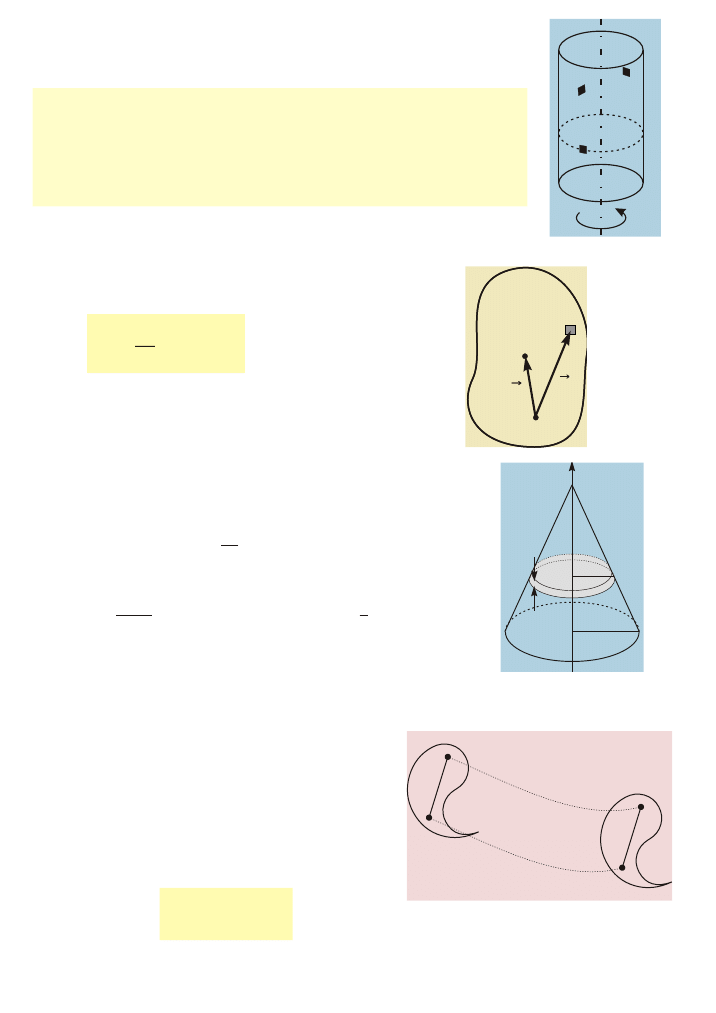
Przyk³ad wyznaczania œrodka masy:
a) prêt (belka), b) obrêcz c) walec; d) kula
e) sto¿ek
D
D
m
R
H
H
x
x
i
i
i
=
-
p
r
2
2
2
(
)
M
V
R H
=
=
r
r
p
1
3
2
.
Œrodek masy bry³y sztywnej
O
r
M
r
s
Dm
i
i
Œrodek masy uk³adu cia³
x
M
m x
®
®
=
å
s
i
i
i =1
N
1
D
M
m
=
å
D
i
i =1
N
O
R
H
r
x
dx
X
Ruch postêpowy bry³y sztywnej
F
M a
®
®
=
z
s
r
M
m r
®
®
=
å
s
i
i
i =1
N
1
D
w
e
Ruch obrotowy bry³y sztywnej
Bry³¹ sztywn¹ nazywamy takie cia³o, w którym odleg³oœci
pomiêdzy poszczególnymi jego elementami nie zmieniaj¹ siê,
niezale¿nie od dzia³aj¹cych si³. Je¿eli bry³a sztywna wiruje wokó³
osi obrotu, to prêdkoœæ k¹towa w i przyspieszenie k¹towe e
wszystkich jej elementów s¹ jednakowe.
A
B
A’
B’
AB || A’B’
Druga zasada dynamiki
dla ruchu postêpowego
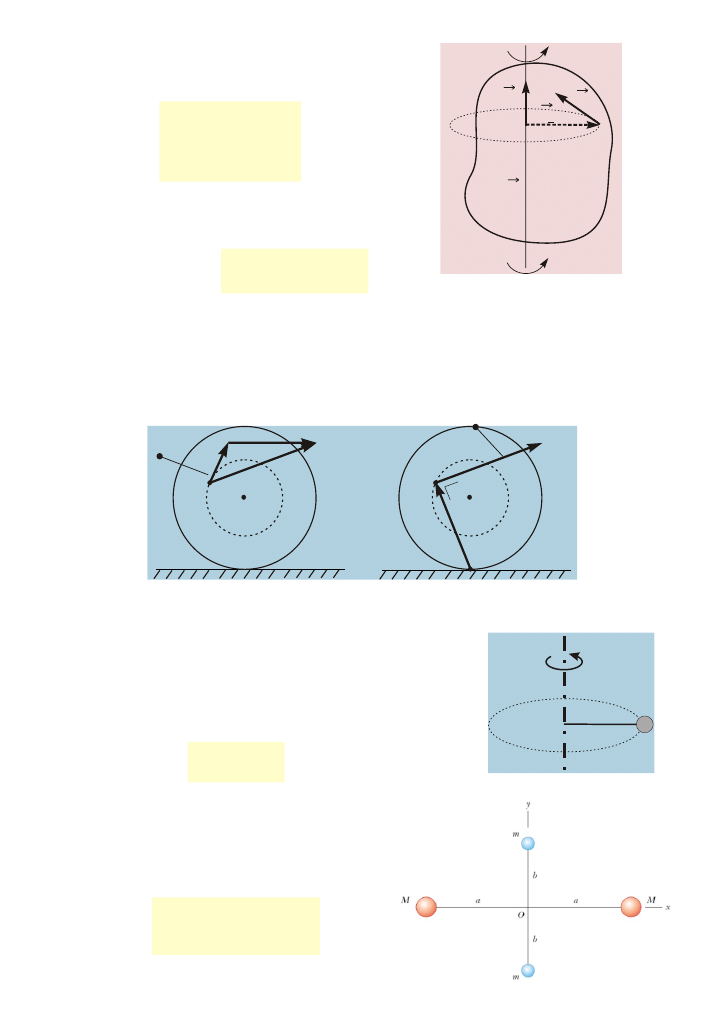
Chwilowa oœ obrotu
– z³o¿enie prêdkoœci v
®
s
i prêdkoœci ruchu obrotowego w
®
®
´ r (o wartoœci wr )
– prêdkoœæ ruchu czysto obrotowego w
®
®
´ r' (o wartoœci wr' )
Moment bezw³adnoœci punktu materialnego
P
O
P
A
w
®
®
´ r
r'
®
v
v
®
®
®
®
=
+
´
s
r
w
v
®
®
®
=
´
w
r'
v
®
s
Ruch obrotowy bry³y sztywnej
v
v
®
®
®
^
^
=
´
=
w
w
r
r
O
w
v
w
P
r
k
k’
Ruch dowolny bry³y sztywnej
v
v
®
®
®
®
=
+
´
s
r
w
Moment bezw³adnoœci cia³a wzglêdem danej osi
m
r
I
mr
=
2
Moment bezw³adnoœci uk³adu punktów materialnych
I
m r
i
N
=
=
å
i i
1
2
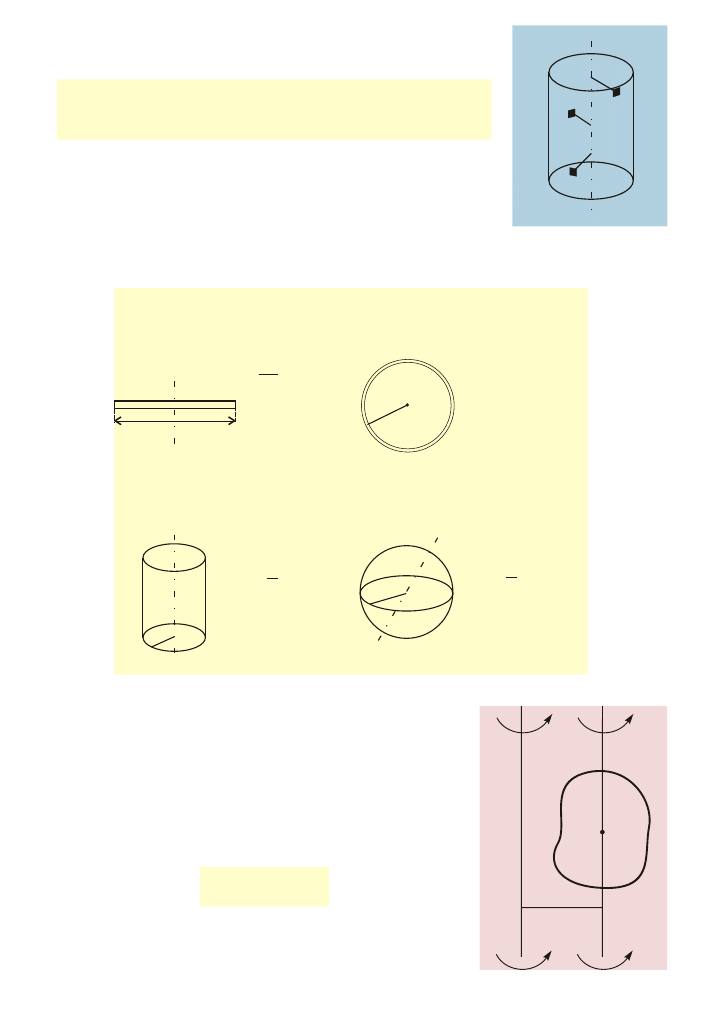
r
i
r
2
r
1
Dm
i
Dm
2
Dm
1
I
m r
m r
m r
m r
m r
=
+
+
+
+
+
=
=
å
D
D
D
D
D
1 1
2
2 2
2
2
2
1
...
...
i i
2
N N
i i
i
N
R
M - masa walca
Moment bezw³adnoœci walca
wzglêdem jego osi symetrii
2
I = M R
w
1
2
Moment bezw³adnoœci kuli
wzglêdem dowolnej osi symetrii
R
M - masa kuli
2
I = M R
k
2
5
R O
Moment bezw³adnoœci cienkiej obrêczy
wzglêdem osi symetrii przechodz¹cej
przez jej œrodek
M - masa obrêczy
Moment bezw³adnoœci prêta
wzglêdem osi symetrii
prostopad³ej do prêta
M - masa prêta
l
2
I = M l
p
1
12
2
I =M R
o
Momenty bezw³adnoœci niektórych bry³
Twierdzenie Steinera
(twierdzenie o osiach równoleg³ych)
S
k
k’
M
k’’
k’’’
d
I
I
Md
=
+
0
2
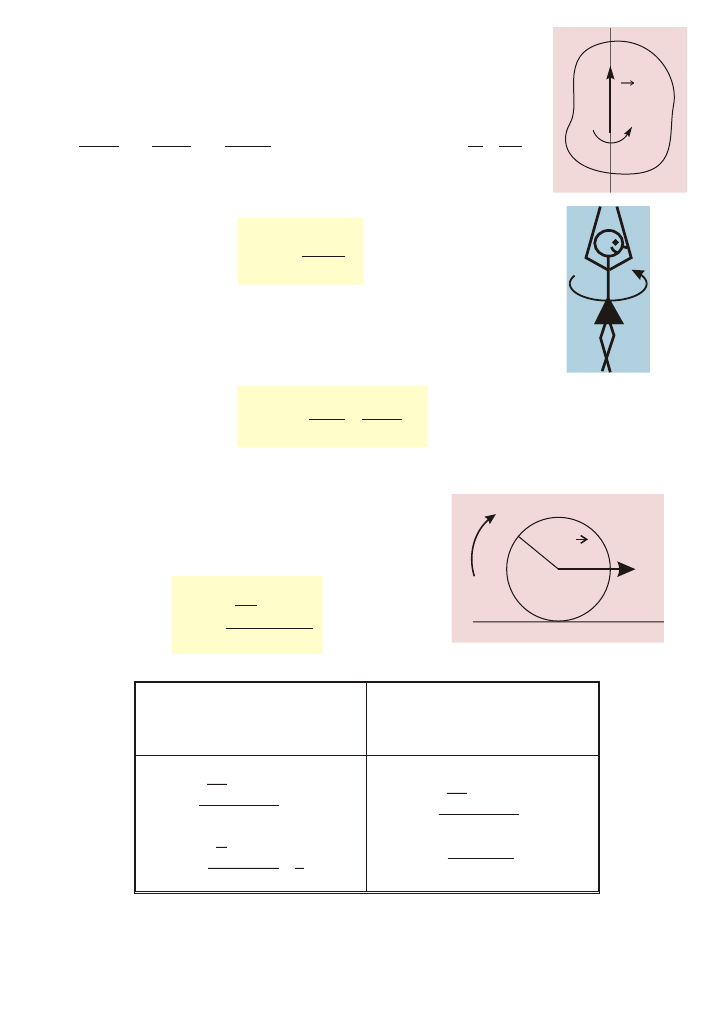
Ca³kowita energia kinetyczna bry³y sztywnej
Energia kinetyczna tocz¹cego siê cia³a
Energia kinetyczna bry³y sztywnej
Energia kinetyczna w ruchu obrotowym wokó³ ustalonej osi
E
I
k
=
w
2
2
k
k’
w
I
E
m
I
s
kC
v
=
+
2
2
2
2
O
w
R
w
v
O
s
E
I
R
m
k, c
v
=
+
æ
è
ç
ö
ø
÷
2
2
2
walca
obrêczy
E
I
R
m
m
m
m
k
v
v
v
=
+
æ
è
ç
ö
ø
÷
=
=
+
æ
è
ç
ö
ø
÷
=
2
2
2
2
2
2
2
3
4
E
I
R
m
m m
m
k
v
v
v
=
+
æ
è
ç
ö
ø
÷
=
=
+
=
2
2
2
2
2
2
(
)
E
m
m
m
m r
k,obr
i
i
N
N
v
v
v
=
+
+
+
+
=
+
D
D
D
D
1
1
2
2
2
1 1
2
2
2
2
...
...
(
...+
+
+
=
D
D
m r
m r
I
i i
N N
2
2
2
2
2
2
...
)
w
w
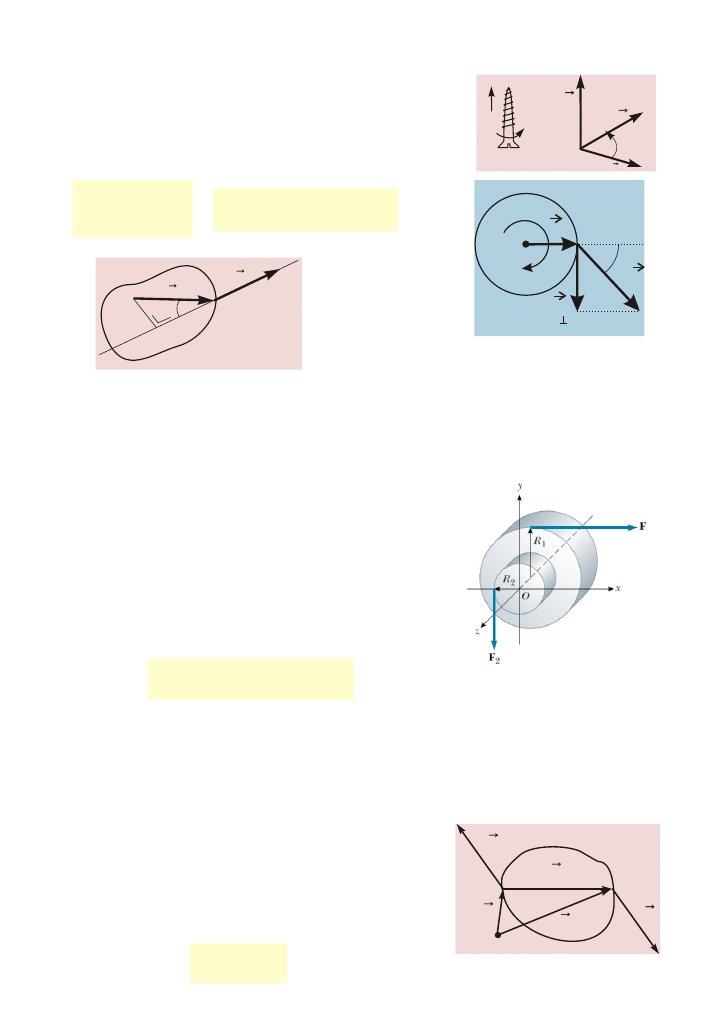
l - ramiê dzia³ania si³y
Moment si³y
Moment si³y wzglêdem danego punktu
O
l
r
1
r
2
F
-F
Moment pary si³
M
r
F
r
F
r
r
F
l F
®
®
®
®
®
®
®
®
®
®
=
´
+
´ -
=
-
æ
è
ç
ö
ø
÷´
= ´
1
2
1
2
(
)
M
r F
®
®
®
= ´
M
r F
r F
=
=
^
sin a
a
M
r
F
M=r F sina =l F
a
O
r
l
F
Moment si³y wzglêdem danej osi
M
l F
||
=
^
a
O
r
F
F
M
M
M
M
=
+
+
+
1
2
...
N
M
M
M
M
N
®
®
®
®
=
+
+ +
1
2
...
M
l
F
®
®
®
= ´
Wypadkowy moment si³
Wypadkowy moment si³ dzia³ajcych wzd³u¿ danej osi
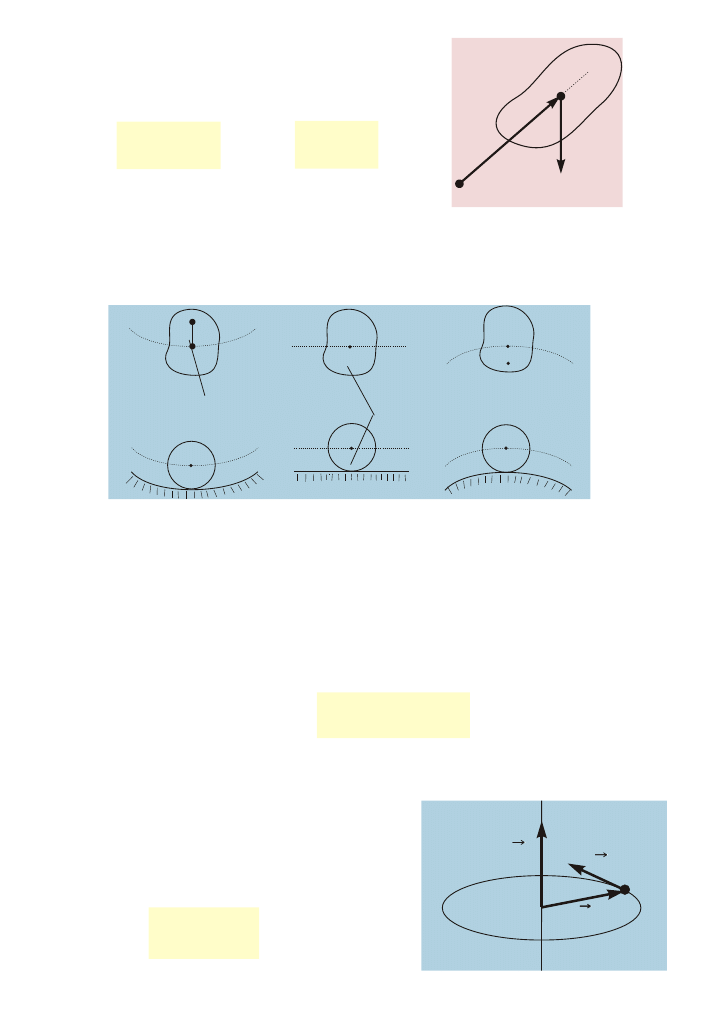
Moment pêdu punktu
r
®
®
^ v L
rm
=
v v
®
®
®
=
´
w
r
Œrodek ciê¿koœci
Rodzaje równowagi
C
O
r
®
c
P
mg
®
®
=
M
r
P
®
®
®
=
´
c
r
r
®
®
=
c
s
C
C
C
C
C
C
równowaga trwa³a
punkt zawieszenia
œrodek ciê¿koœci
cia³a
równowaga obojêtna
równowaga chwiejna
Moment pêdu punktu w ruchu po okrêgu
L
m r
®
®
=
2
w
Moment pêdu
v
L
r
m
L
r
p
r
m
®
®
®
®
®
= ´
= ´
v
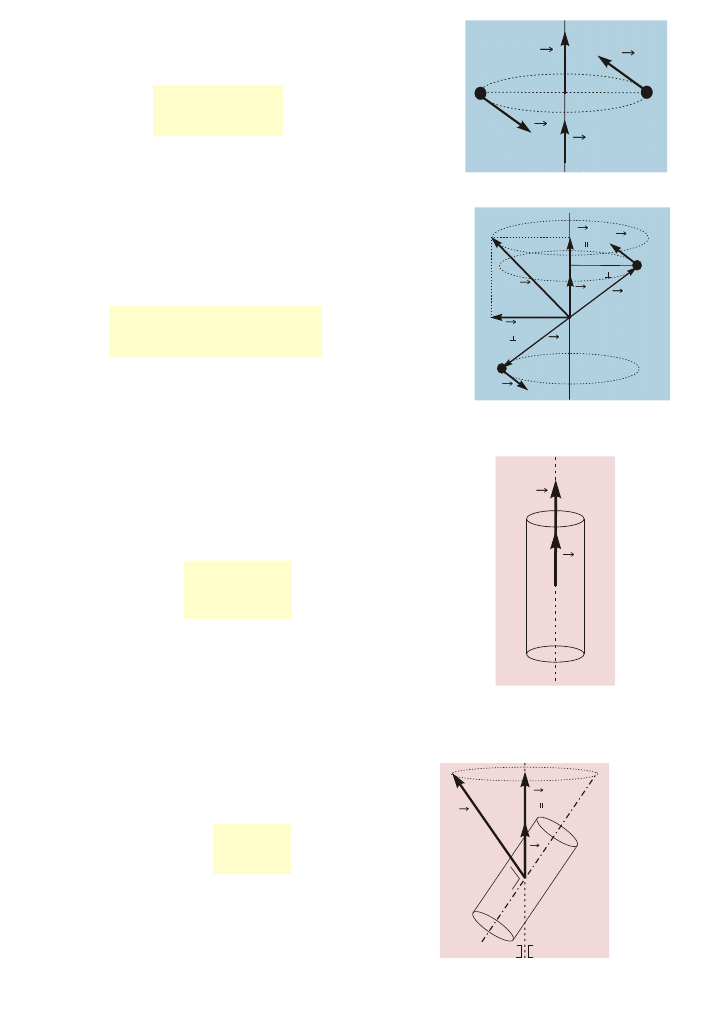
k’
w
r
O
k
L
L
L
r
1
m
m
v
2
v
1
r
2
L
r
m
m r
®
®
®
®
®
=
´
=
´
2
2
1
1
2
2
v
v
Moment pêdu cia³a w ruchu obrotowym wzglêdem osi swobodnej
L
I
®
®
= w
w
L
k
k’
Moment pêdu cia³a w ruchu obrotowym
wzglêdem nieruchomej osi
wymuszonej
L
I
®
®
=
||
w
w
L
L
wymuszona oœ brotu
Moment pêdu bry³y sztywnej
L
L
m r
®
^
®
^
®
¹
=
0
2
2
||
w
Moment pêdu dwóch punktów przeciwleg³ych
v
1
w
m
r
m
v
2
L
O
L
m r
®
®
= 2
2
w
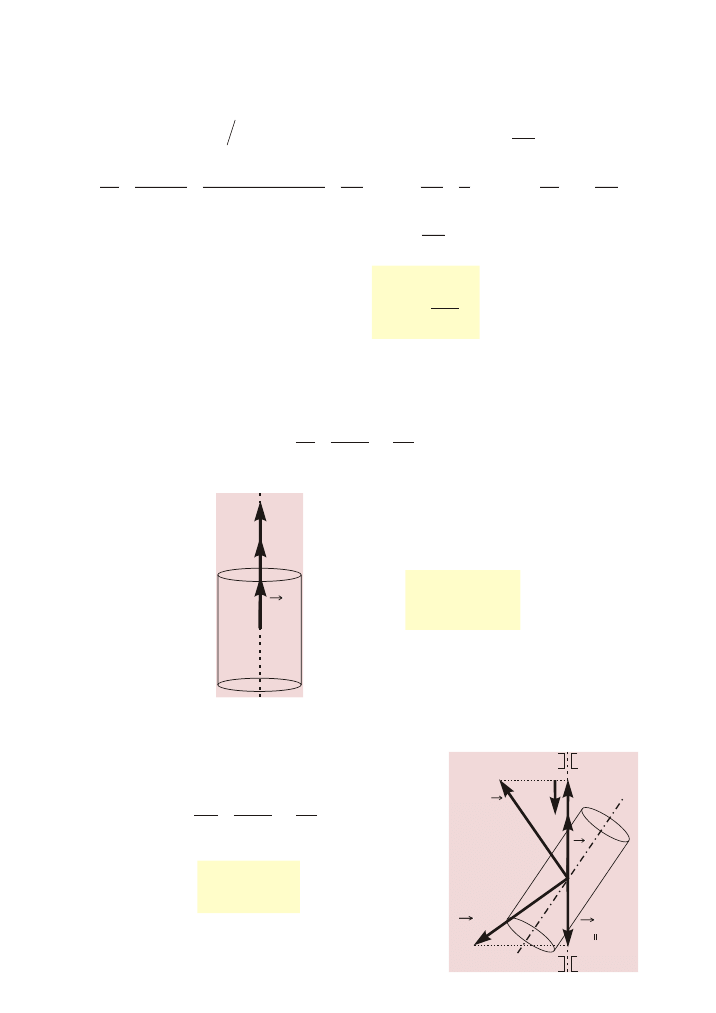
Punkt materialny o masie
m
F
p
t
®
®
= D
D , ( p
m
®
®
=
v) M
r F
r
p
t
®
®
®
®
®
= ´
= ´
D
d
D
D
D
D
D
D
D
D
D
D
L
t
r
p
t
r
r
p
p
t
r
t
p
r
®
®
®
®
®
®
®
®
®
®
=
´
=
+
´
+
=
´
+ ´
(
)
(
) (
)
p
t
m
p
p
r
p
t
r
p
t
®
®
®
®
®
®
®
=
´
+ ´
= ´
D
D
D
D
D
1
p p
®
®
´
= 0
Þ
M
L
t
®
®
=
D
D
L
I
®
®
= w
M
L
t
I
t
I
t
I
®
®
®
®
®
=
=
=
=
D
D
D
D
D
D
(
)
w
w
e
M
L
t
I
t
I
t
I
||
||
(
)
®
®
®
®
®
=
=
=
=
D
D
D
D
D
D
w
w
e
Druga zasada dynamiki w ruchu obrotowym bry³y sztywnej
Druga zasada dynamiki dla ruchu obrotowego bry³y wzglêdem osi swobodnej
w
D
D
L
I
®
®
=
w
L
I
®
®
= w
D
D
L
M
t
®
®
=
M
I
®
®
=
e
Druga zasada dynamiki w ruchu obrotowym wokó³ wymuszonej osi nieruchomej
w
L
M
M
L
I
®
®
=
||
w
M
I
®
®
=
||
e
M
L
t
®
®
=
D
D
Druga zasada dynamiki dla ruchu obrotowego
bry³y sztywnej o momencie bezw³adnoœci I
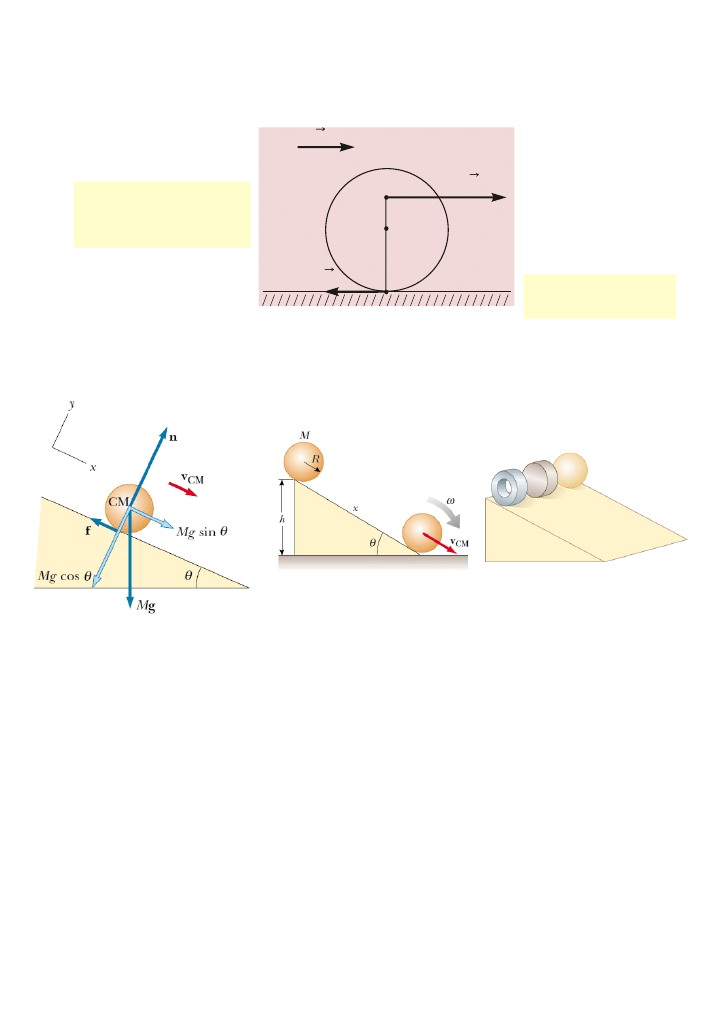
Druga zasada dynamiki przy toczeniu siê cia³ – przyk³ady
v
O
R
O
F
T
r
F
T
ma
Fr
TR
I
s
-
=
+
=
O
e
F R
r
I
(
)
+
= e
ruch obrotowy
z³o¿enie ruchu postêpowego
i obrotowego
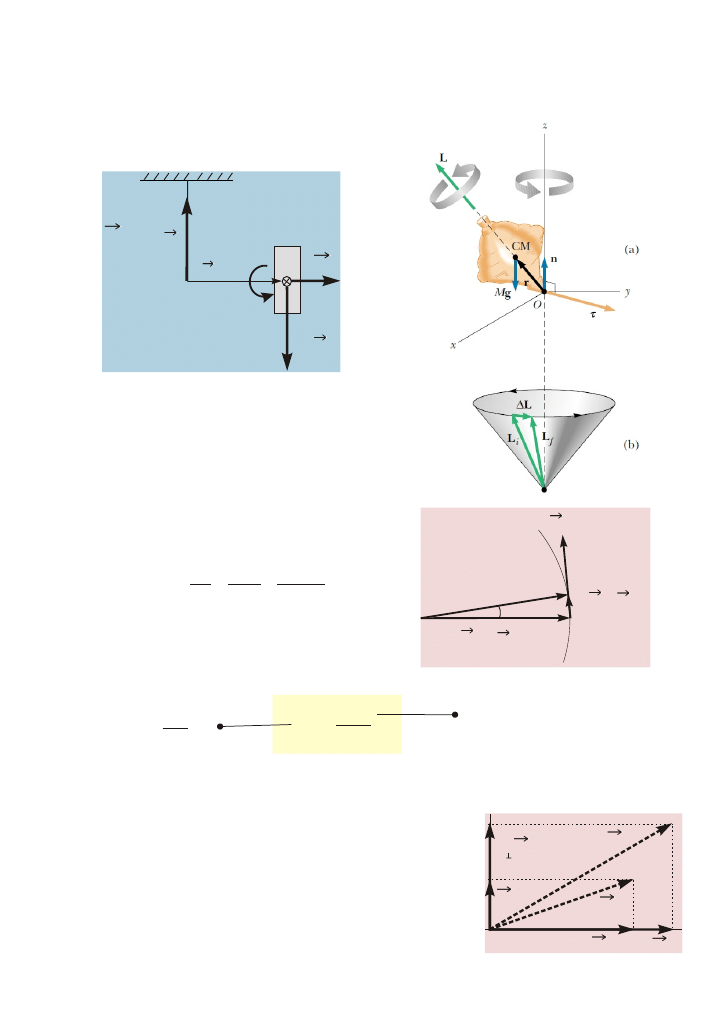
¯yroskop - cia³o o symetrii cylindrycznej obracaj¹ce siê z du¿¹ prêdkoœci¹ k¹tow¹ wzglêdem
osi symetrii
D
D
D
D
j
w
w
=
=
=
L
L
M t
I
mg l t
I
Precesja ¿yroskopu
L=I w
Dj
M
DL=MDt
W =
m gl
I w
W
D
D
=
j
t
l
r
=
®
| |
w
L
I w
w
C
I W
W
F
mg
N
=
F = -mg
N
r
mg
w
M
r m g
®
®
®
= ´
¯yroskop
Nutacja
Ruch ¿yroskopu jest z³o¿eniem:
– ruchu obrotowego wokó³ osi symetrii,
– ruchu precesyjnego, podczas którego wektor momentu pêdu porusza
siê po okrêgu,
– ruchu osi symetrii ¿yroskopu poruszaj¹cej siê
po pobocznicy sto¿ka wokó³ wektora L
®
.
Ten ostatni rodzaj ruchu nazywa siê nutacj¹.
M
®
= 0 Þ L
®
= const.
Dla obrotu dooko³a sta³ej osi
L
I
=
=
w const
Dla obrotu dooko³a sta³ej osi
L
I
i
N
i
N
i
i
i
const
=
=
å
å
=
=
1
1
w
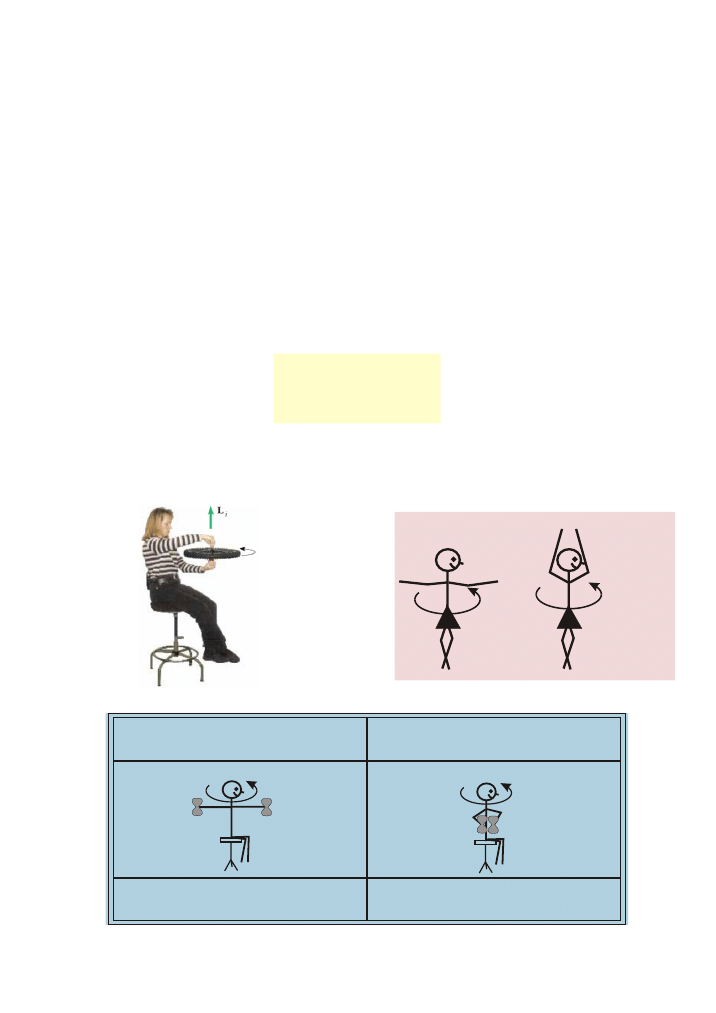
Przyk³ady:
Zasada zachowania momentu pêdu uk³adu cia³
I
I
i
i
N
j
j
M
w
w
®
=
®
=
å
å
=
i
j
1
1
Zasada zachowania momentu pêdu cia³a
w
1
w
2
w
1
>
I
1
I
1
I
2
>
Cz³owiek trzyma odwa¿niki
mo¿liwie jak najdalej od tu³owia
=
przed
1
1
I w
Po zbli¿eniu odwa¿ników do tu³owia
w
1
=
po
2
2
I w
w
2
L
L
I
I
1
1
2
2
w
w
=
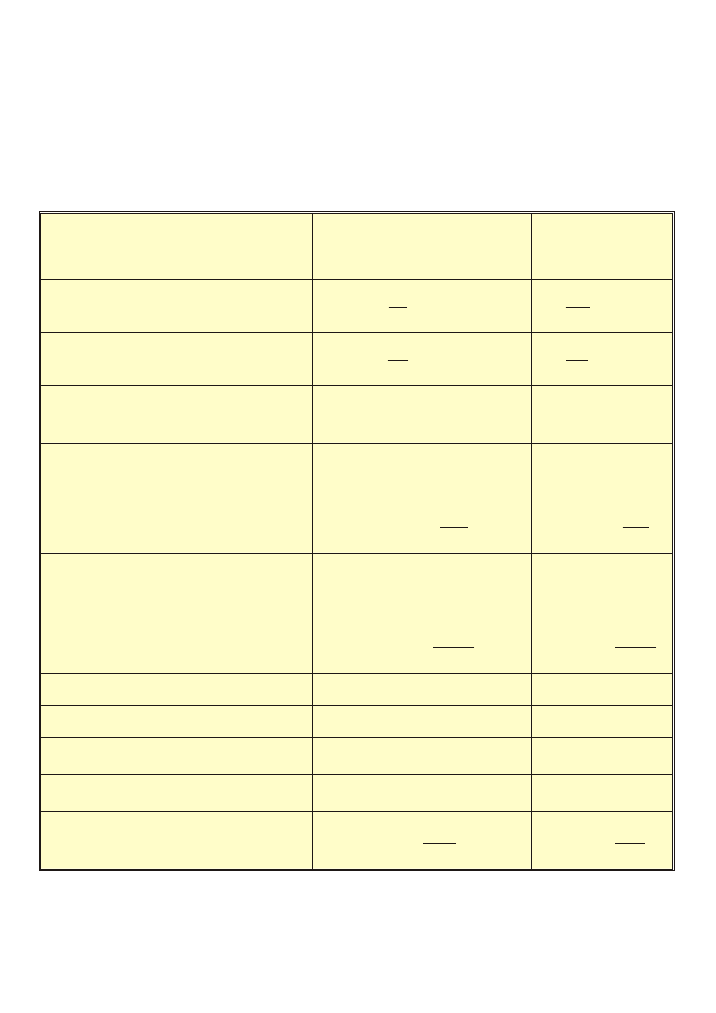
Ruch postêpowy
Ruch obrotowy
wokó³ ustalonej osi
obrotu
prêdkoœæ
v =
®
D
D
D
s
t
t
,
0
w
a
=
®
D
D
D
t
t
,
0
przyspieszenie
a
t
t
=
®
D
D
D
v
,
0
e
w
=
®
D
D
D
t
t
,
0
ruch jednostajny
v
const
=
s
t
= v
w = const
a
w
= t
ruch jednostajnie przyspieszony
a = const
v
v
0
=
+ a t
s
t
a t
=
+
v
0
2
2
e = const
w w
e
=
+
0
t
a
w
e
=
+
0
2
2
t
t
ruch jednostajnie opóŸniony
a
op
const
=
v
v
0
op
=
- a t
s
t
a
t
=
-
v
op
0
2
2
e
op
const
=
w w
e
=
-
0
op
t
a
w
e
=
-
0
2
2
t
t
op
masa / moment bezw³adnoœci
m
I
si³a / moment si³y
F
M
II zasada dynamiki Newtona
F
m a
=
M
I
= e
pêd / moment pêdu cia³a
p
m
=
v
K
I
= w
energia kinetyczna
E
m
k
v
=
2
2
E
I
k, obr
=
w
2
2
Porównanie wzorów opisuj¹cych ruch postêpowy prostoliniowy i obrotowy cia³a
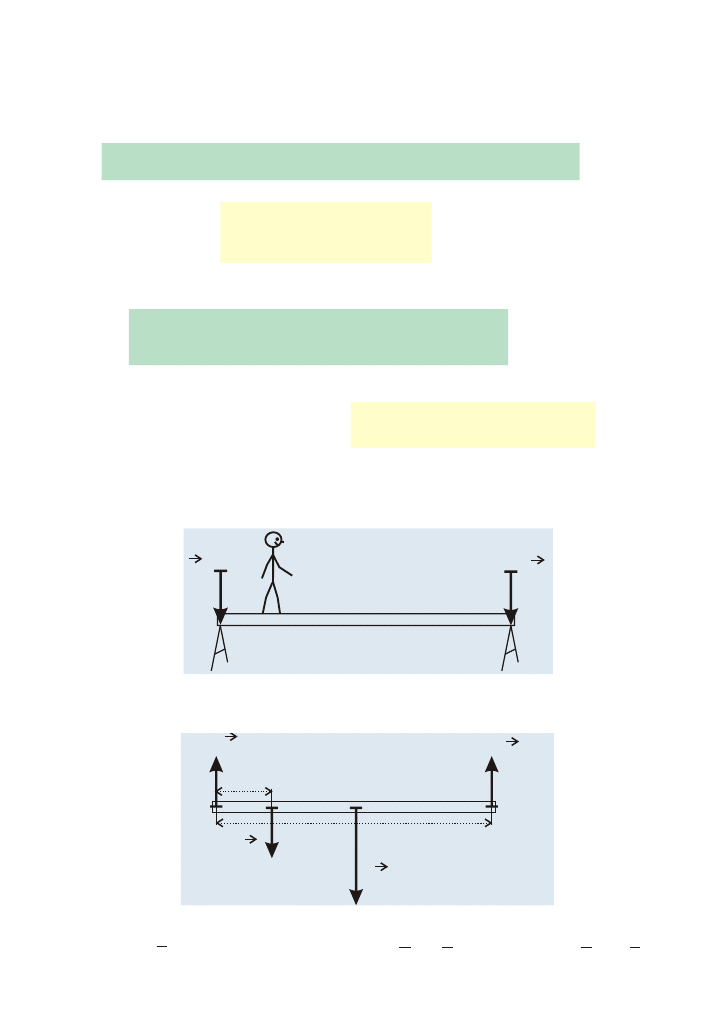
Warunki równowagi cia³a
Statyka
F
F
F
1
2
0
®
®
®
+
+ +
=
...
N
M
M
M
1
2
0
+
+ +
=
...
N
M
M
M
M
N
®
®
®
®
=
+
+ +
1
2
...
Wypadkowa wszystkich si³ dzia³aj¹cych na cia³o jest równa zeru
Suma algebraiczna momentów wszystkich si³
wzglêdem dowolnie wybranej osi jest równa zeru
N
L
N
P
F
L
F
P
P
Q
l
x
Przyk³ad równowagi cia³a
N
F
L
=
L
P x
Q
l
F l
+
=
2
P
P
Q
F
F
+
=
+
L
P
N
F
L
=
P
F
x
l
P
Q
L
=
+
1
2
i F
x
l
P
Q
P
=
-
æ
è
ç
ö
ø
÷
+
1
1
2
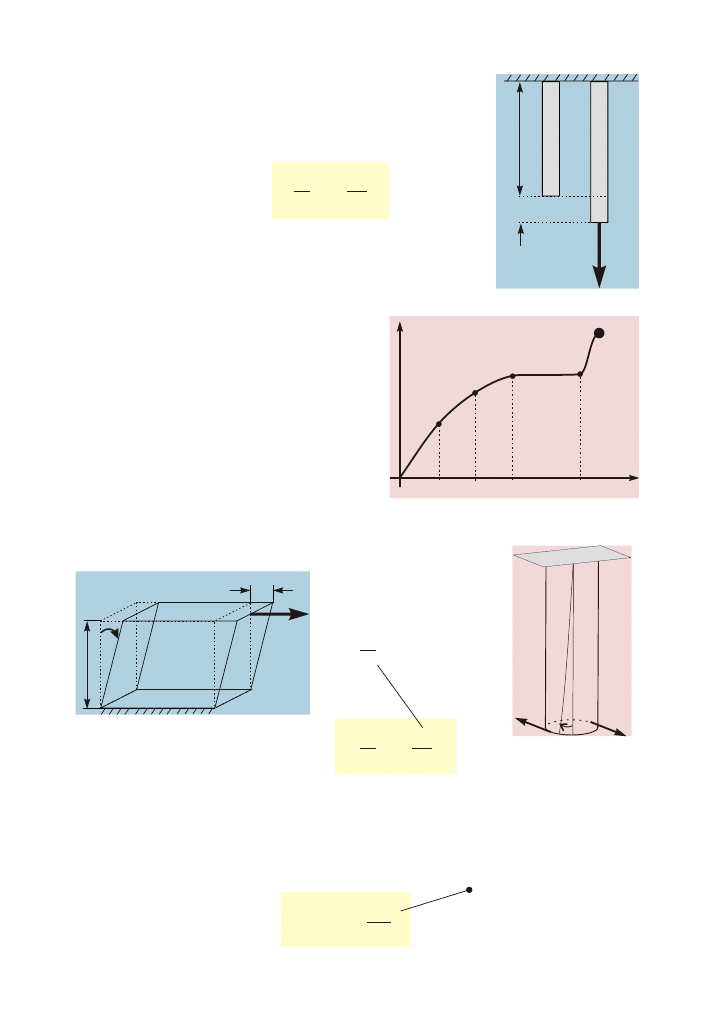
0-A
–
s
e
µ
A-B – prawa Hooke'a nie mo¿na stosowaæ
B – granica sprê¿ystoœci
C-D – obszar plastycznoœci
E – granica wytrzyma³oœci
W³asnoœci sprê¿yste cia³ sta³ych
Prawo Hooke’a dla wyd³u¿eñ
F
S
E
l
l
=
D
s
e
= E
F
l
Dl
F
g
Dl
l
S
g
F
F
s
e
A
D
C
B
E
0
Prawo Hooke’a dla odkszta³ceñ postaciowych
F
S
G
l
l
=
D
Dl
l
=
@
tan g
g
s
g
= G
Prawo Hooke’a dla cieczy i gazów
D
D
p
K
V
V
= -
DV<0