Politechnika Świętokrzyska w Kielcach |
||||
Laboratorium elektrotechniki |
||||
Ćwiczenie Nr. |
Temat: Badanie rezonansu napięć i prądów. |
Zespół Nr 2 1.Cholewiński Paweł 2.Czyż Piotr 3.Kołodziejski Jacek |
||
Data wykonania ćwiczenia:
25.10.2005r. |
Ocena:
|
Wydział: WEAiI gr.204B |
||
1. Cel ćwiczenia.
Celem ćwiczenia jest wyznaczenie częstotliwości rezonansowej, charakterystyk częstotliwościowych i wykresów wektorowych prądów i napięć w trakcie trwania rezonansu oraz dla częstotliwości różniących się od częstotliwości rezonansowej.
2. Wykaz przyrządów.
- generator z regulowaną częstotliwością
- amperomierze - sztuk 4
- woltomierze - sztuk 4
- płytka z kondensatorem C = 9,3 μF, cewką o indukcyjności L = 330 mH i rezystancją R = 114,6 Ω
- przewody łączeniowe.
3. Schemat pomiarowy:
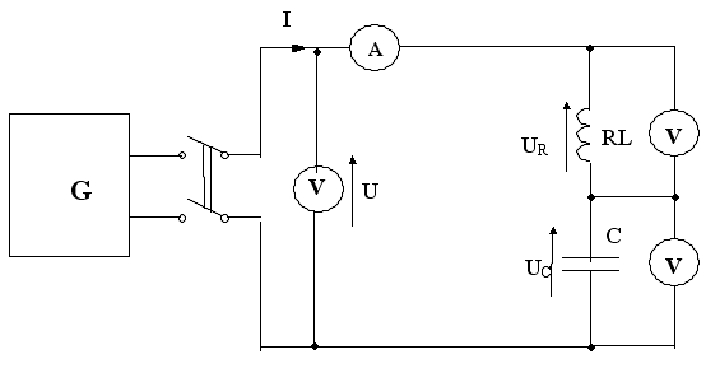
Schemat pomiarowy do badania rezonansu napięć:
Schemat pomiarowy do badania rezonansu prądów:
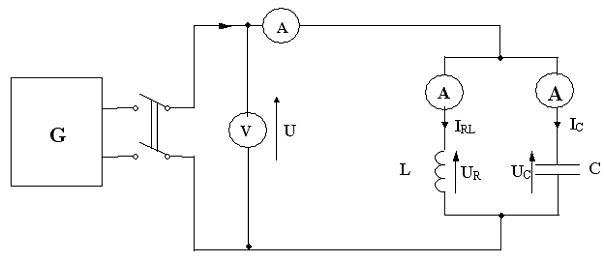
4. Tabele pomiarowe.
Rezonans napięć:
U = 0,5 V R = 114,6 Ω L = 330 mH C = 9,3μF |
||||||||
|
POMIARY |
OBLICZENIA |
||||||
Lp. |
f [Hz] |
I[mA] |
URL [mV] |
UC [mV] |
UR [mV] |
UL [mV] |
|Z| [Ω] |
ϕ |
1 |
20 |
0,62 |
82 |
530 |
|
|
|
|
2 |
30 |
1,03 |
141 |
562 |
|
|
|
|
3 |
40 |
1,49 |
222 |
607 |
|
|
|
|
4 |
50 |
2,15 |
376 |
684 |
|
|
|
|
5 |
60 |
2,98 |
580 |
784 |
|
|
|
|
6 |
65 |
3,42 |
678 |
830 |
|
|
|
|
7 |
70 |
3,81 |
780 |
852 |
|
|
|
|
8 |
72 |
3,94 |
843 |
855 |
|
|
|
|
9 |
74 |
4,03 |
880 |
850 |
|
|
|
|
10 |
76 |
4,09 |
912 |
840 |
|
|
|
|
11 |
78 |
4,11 |
936 |
822 |
|
|
|
|
12 |
80 |
4,11 |
976 |
802 |
|
|
|
|
13 |
82 |
4,09 |
967 |
779 |
|
|
|
|
14 |
84 |
4,05 |
971 |
753 |
|
|
|
|
15 |
86 |
3,99 |
973 |
728 |
|
|
|
|
16 |
88 |
3,92 |
972 |
697 |
|
|
|
|
17 |
90 |
3,82 |
965 |
665 |
|
|
|
|
18 |
100 |
3,37 |
913 |
532 |
|
|
|
|
19 |
120 |
2,57 |
777 |
343 |
|
|
|
|
20 |
150 |
1,78 |
674 |
186 |
|
|
|
|
U = 0,5 V R = 114,6 Ω L = 0,33 H C = 9,3μF |
||||||
|
f |
ϕ |
I |
IL |
IC |
|Z| |
Lp. |
Hz |
° |
mA |
mA |
mA |
Ω |
1 |
20 |
-12,09 |
3,68 |
3,6 |
0,5 |
106,68 |
2 |
30 |
-14,95 |
3,19 |
3,3 |
0,8 |
106,13 |
3 |
40 |
-15,95 |
2,68 |
3,1 |
1,1 |
106,31 |
4 |
50 |
-11,61 |
2,17 |
2,7 |
1,4 |
106,46 |
5 |
60 |
-1,31 |
1,81 |
2,5 |
1,8 |
106,18 |
6 |
70 |
15,31 |
1,51 |
2,2 |
2,1 |
105,29 |
7 |
72 |
18,76 |
1,48 |
2,2 |
2,2 |
105,03 |
8 |
74 |
18,38 |
1,46 |
2,2 |
2,2 |
104,76 |
9 |
76 |
25,97 |
1,45 |
2,1 |
2,3 |
104,46 |
10 |
78 |
30,02 |
1,45 |
2 |
2,3 |
104,14 |
11 |
80 |
33,57 |
1,45 |
2 |
2,4 |
103,79 |
12 |
84 |
41,15 |
1,49 |
1,9 |
2,5 |
103,04 |
13 |
88 |
44,44 |
1,53 |
1,9 |
2,6 |
102,21 |
14 |
90 |
51,07 |
1,57 |
1,8 |
2,7 |
101,78 |
15 |
100 |
61,46 |
1,8 |
1,7 |
3 |
99,36 |
16 |
120 |
75,88 |
2,4 |
1,4 |
3,6 |
93,78 |
17 |
150 |
83,74 |
3,51 |
1,1 |
4,5 |
84,88 |
5. Przykładowe obliczenia.
REZONANS NAPIĘĆ
Napięcie na rezystancji cewki:
![]()
![]()
Napięcie na indukcyjności:
![]()
Dla f =20 Hz i I= 0,62 mA:
ω = 2⋅π⋅f = 125,66 rad/s
XL = ω⋅L = 41,47 Ω
![]()
Moduł impedancji:
Dla f =20 Hz i I= 0,62 mA:
ω = 2⋅π⋅f = 125,66 rad/s
XL = ω⋅L = 41,47 Ω
XC = 1/ωC = 855,7 Ω
R = 114,6 Ω
![]()
![]()
Kąt ϕ:
![]()
Dla f =20 Hz
ω = 2⋅π⋅f = 125,66 rad/s
XL = ω⋅L = 41,47 Ω
XC = 1/ωC = 855,7 Ω
R = 114,6 Ω
![]()
Częstotliwość rezonansowa obliczona:
![]()
Różnica częstotliwości policzonej i zmierzonej:
![]()
REZONANS PRĄDÓW
Moduł impedancji:
Dla f =20 Hz
ω = 2⋅π⋅f = 125,66 rad/s
XL = ω⋅L = 41,47 Ω
XC = 1/ωC = 855,7 Ω
R = 114,6 Ω
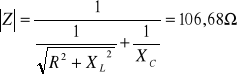
Kąt ϕ:
Przy założeniu, że rezystancja znajduje w gałęzi z cewką wykonujemy następujące obliczeia:
![]()
![]()
gdzie IL1 - składowa urojona prądu IL dla danej chwili
![]()
IL2 - składowa rzeczywista prądu IL dla danej chwili
![]()
IP - składowa urojona wypadkowa układu dla danej chwili
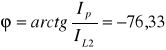
Obliczanie częstotliwości rezonansowej
![]()
Różnica częstotliwości policzonej i zmierzonej:
![]()
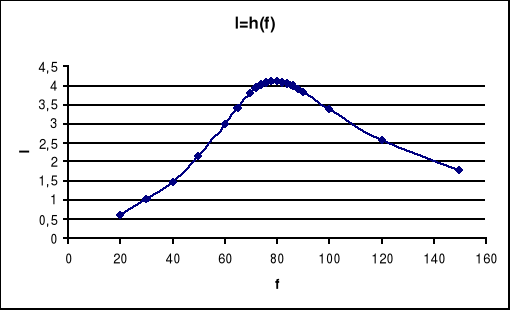
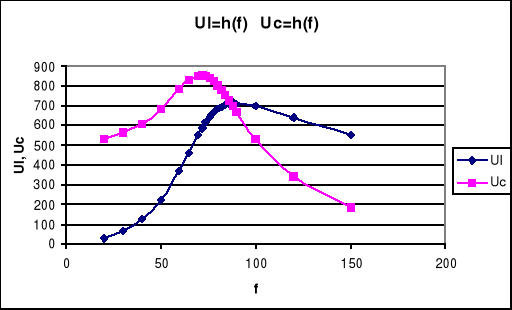
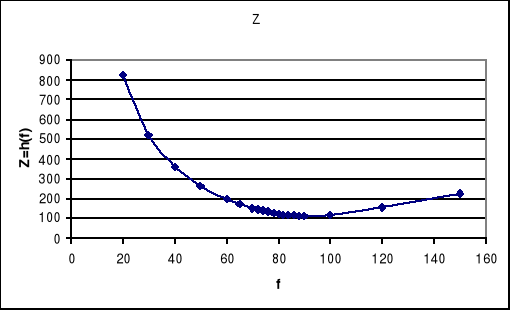
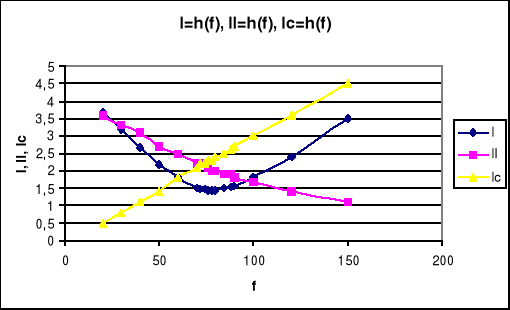
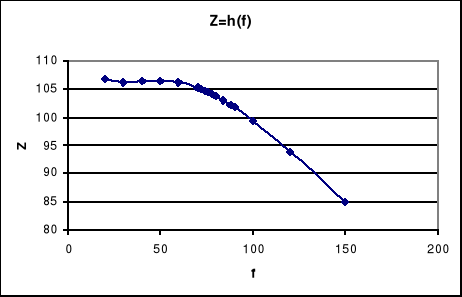
6. Krzywe rezonansowe I,UL, UC, Z w funkcji częstotliwości.
Dla rezonansu napięć:
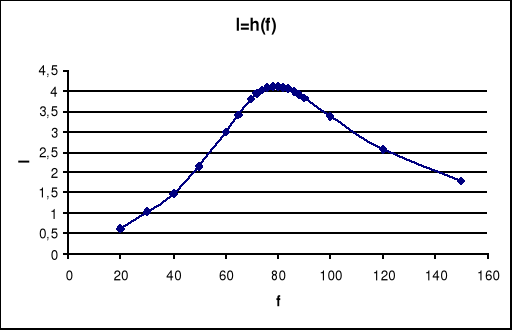
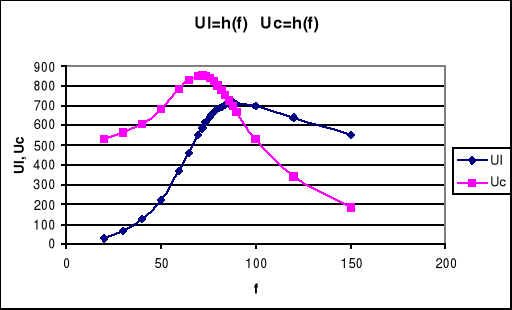
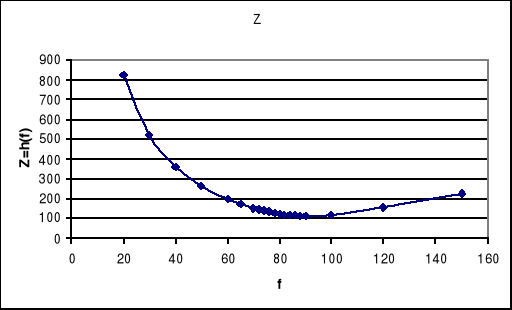
Dla rezonansu prądów:
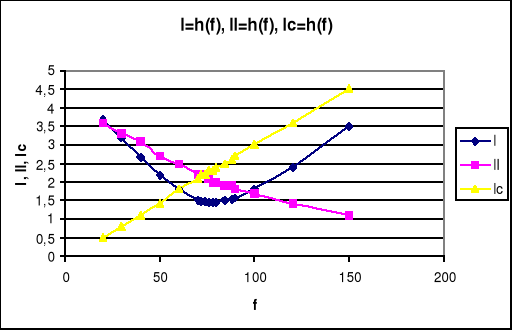
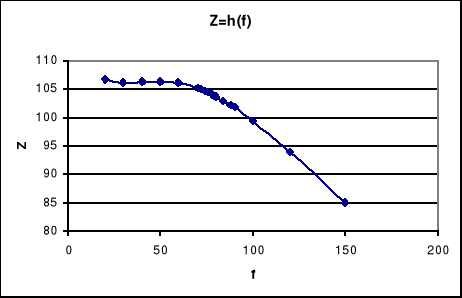
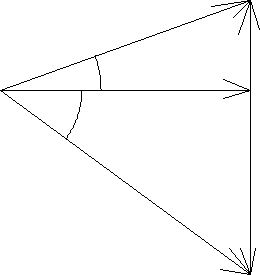
7. Wykresy wektorowe.
Dla rezonansu szeregowego:
UC=UCMAX
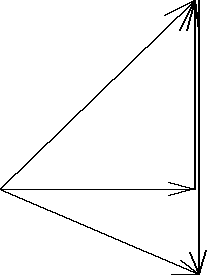
UC=UL
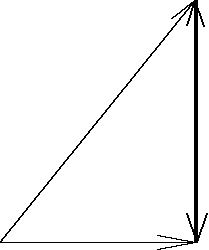
UL=ULMAX

Dla rezonansu równoległego:
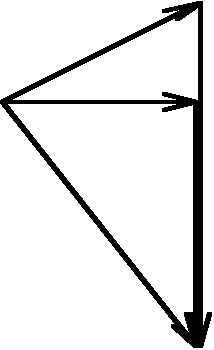
W trakcie rezonansie:
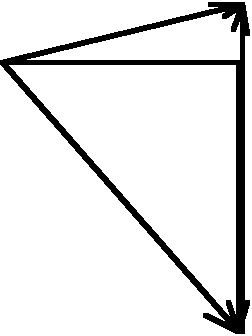
Poniżej częstotliwości rezonansowej (f = 70 Hz):
Powyżej częstotliwości rezonansowej (f = 88 Hz):
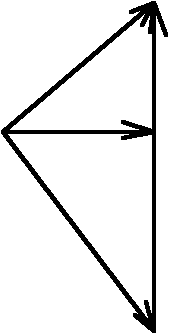
8.Wnioski.
Z przeprowadzonych badań i z używanych podczas nich elementów wnioskujemy, że rezonans występuje w obecności elementów LC. Za pomocą obliczeń wyznaczyliśmy częstotliwość rezonansową która różni się od tej uzyskanej w wyniku przeprowadzonych pomiarów. Przypuszczamy, że przyczyną tego było nie uwzględnienie rezystancji i innych pasożytniczych wielkości. Częstotliwość w obwodzie szeregowym i równoległym przy zastosowaniu tych samych elementów jest identyczna, gdyż zależy ona od wartości użytych elementów LC. Przebieg prądu w funkcji częstotliwości dla rezonansu szeregowego charakteryzuje się tym, iż prąd osiąga maksimum przy częstotliwości rezonansowej. Wartości napięć na cewce i kondensatorze, inaczej niż w teorii, mają swe maksima w pobliżu częstotliwości rezonansowej. Jest to spowodowane występowaniem wartości pasożytniczych. Moduł impedancji osiąga swe minimum w funkcji częstotliwości przy f = f rezonansowej. Przy rezonansie prąd ograniczony jest tylko wartością rezystancji i w związku z tym nie jest przesunięty w fazie z napięciem.
Przy rezonansie równoległym prąd osiąga wartość minimalną. Częstotliwość rezonansowa zw teorii zachodzi gdy BC = BL, ale w praktyce nie jest tak do końca. Moduł impedancji osiąga maksimum w okolicach częstotliwości rezonansowej. Tak jak w rezonansie szeregowym częstotliwość rezonansowa różni się od tej obliczonej. W czasie zmiany częstotliwości zmieniał się charakter obwodu i kąty między prądami a napięciami zasilającymi. Przy obliczeniach kąta ϕ uwzględniliśmy rezystor połączony w szereg z cewką. W związku na samym początku musieliśmy liczyć przesunięcie między prądem a napięciem w tej gałęzi a potem dopiero całego obwodu wraz z kondensatorem. Dlatego nie skorzystaliśmy ze wzoru na wartość ϕ w połączeniu równoległym R, L, C. Obliczenia nasze mimo, że wykonane w inny sposób są prawidłowe.
Wyszukiwarka
Podobne podstrony:
Kopia (2) pchrezonans, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika,
Kopia pchrezonans, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika, rez
pchrezonans nasze, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika, rez
NNN rezonans-protokół, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika,
Sprawozdanie cw1, Energetyka I stopień PŚk, sem1 Elektronika, sem1 elektronika lab, ćw1 diody labora
NNN Badanie rezonansu gotowe +wykresall, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratoriu
GGG rezonas-protokół, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika,
GGG rezonas, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika, rezonans
rezonans-protokół, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika, rez
ca-kowy Fourier, Energetyka I stopień PŚk, sem1 Elektrotechnika, Laboratorium elektrotechnika, teori
Źródła napięciowe i prądowe, Energetyka I stopień PŚk, sem1 Elektrotechnika, ćwiczenia elektrotechni
projekt sily od kogoś, Energetyka I stopień PŚk, sem3 Instalacje Elektryczne, sem3 IE Projekt
sem2 Lista energ12, Energetyka I stopień PŚk, sem2 Matematyka 2, matma1 (oddane)
odp I seria, Energetyka I stopień PŚk, sem2 Materiałoznastwo
Zarz R 65 12 Regulamin zal 6, Energetyka I stopień PŚk, sem3 Energoelektronika, sem3 energo materiał
Teorie mocy w obwodach prądu przemiennego, Energetyka I stopień PŚk, sem3 Energoelektronika, sem3 en
sprawko 4, PWr W9 Energetyka stopień inż, IV Semestr, Maszyny i urządzenia elektryczne, Laboratorium
więcej podobnych podstron