BADANIA OPERACYJNE
ĆWICZENIA
Programowanie liniowe
Literatura:
1. Jacek Błażewicz, Wojciech Celary, Roman Słowiński, Jan Węglarz: Badania operacyjne dla informatyków. WNT, Warszawa 1983.
2. Saul I. Gass: Programowanie liniowe - Zastosowania. PWN, Warszawa 1976.
3. Stanisław Krawczyk: Programowanie matematyczne. PWE, Warszawa 1980.
4. Zbigniew Jędrzejczyk, Karol Kukuła, Jerzy Skrzypek, Anna Walkosz: Badania operacyjne w przykładach i zadaniach. PWN, Warszawa 1997.
WYBRANE ZASTOSOWANIA PROGRAMOWANIA LINIOWEGO
Zagadnienie o diecie (zadanie o mieszance)
Mamy do dyspozycji ![]()
różnych artykułów spożywczych (np. chleb, mięso, owoce) odpowiednio w liczbie jednostek. Dzienna dieta powinna zapewnić spożycie ![]()
składników odżywczych (np. tłuszcze, białko, witaminy) w ilościach nie mniejszych niż jednostek. Znana jest macierz (tablica dietetyczna)
,
której element ![]()
oznacza liczbę jednostek i-tego składnika odżywczego wchodzących w skład jednostki j-tego artykułu spożywczego. Znane są również ceny poszczególnych artykułów spożywczych.
Należy określić, jakie artykuły spożywcze i w jakich ilościach powinny wchodzić w skład diety, aby dieta spełniała powyższe wymagania i aby jej całkowity koszt był najmniejszy.
Zad. 1.1. Do karmienia bydła stosuje się między innymi dwa rodzaje kiszonek jako uzupełnienie paszy treściwej. Zasoby kiszonek kształtują się w taki sposób, że w ciągu doby można zużywać 16 kg I rodzaju kiszonki i 10 kg II rodzaju. Obydwa rodzaje kiszonek zawierają dwa istotne dla hodowli składniki, których ilości dostarczone zwierzętom w ciągu doby nie mogą być dowolne. Składnika ![]()
należy dostarczyć bydłu co najwyżej 3.3 kg, a składnika ![]()
co najmniej 2.6 kg w ciągu doby. Procentowa zawartość tych składników w obydwu rodzajach kiszonek przedstawia się następująco
|
Procentowa zawartość składników w kiszonce |
|
|
|
|
I rodzaj kiszonki |
30 |
20 |
II rodzaj kiszonki |
10 |
20 |
Wyznaczyć ilości poszczególnych rodzajów kiszonek, jakie należy dodać do paszy treściwej, aby koszt takiego uzupełnienia był minimalny. Koszt produkcji 1 kg I rodzaju kiszonki wynosi 2 zł, a koszt produkcji 1 kg II rodzaju kiszonki wynosi 5 zł.
Zadanie ustalenia optymalnej struktury produkcji
Firma dysponuje ![]()
rodzajami czynników wytwórczych (surowce, maszyny, pracownicy) odpowiednio w ilościach jednostek, produkując ![]()
wyrobów. Firma powinna produkować nie mniej niż ![]()
i nie więcej niż ![]()
jednostek j-tego wyrobu (![]()
). Produkcja jednostki j-tego wyrobu daje przedsiębiorstwu zysk równy ![]()
jednostek pieniężnych.
Znana jest macierz
,
której element ![]()
oznacza liczbę jednostek i-tego czynnika wytwórczego potrzebnych do wytworzenia jednostki j-tego wyrobu. Należy ustalić taki asortyment produkcji firmy (należy obliczyć ile jednostek każdego wyrobu powinna wytwarzać firma), aby produkcja przynosiła firmie maksymalny zysk.
Zad. 2.1. Zakład produkuje dwa wyroby, zużywając do tego celu pewną ilość środków produkcji, z których cztery: energia elektryczna, stal, drewno oraz praca są limitowane. Zużycie środków produkcji na jednostkę wyrobu oraz zasoby poszczególnych środków produkcji są podane w poniższej tabeli.
|
Zużycie środków produkcji na jednostkę wyrobu |
|
|
|
|
Energia |
Stal |
Drewno |
Praca |
Wyrób I |
5 |
5 |
6 |
10 |
Wyrób II |
25 |
10 |
0 |
10 |
Zasoby środków produkcji |
1200 |
600 |
420 |
900 |
Ile poszczególnych wyrobów powinien produkować zakład, aby zysk jego był maksymalny, jeśli zysk jednostkowy wynosi:
- z produkcji wyrobu I 10 zł,
- z produkcji wyrobu II 20 zł ?
Zagadnienie przydziału
Wytwórca produkuje ![]()
wyrobów na ![]()
urządzeniach. Zakładamy, że każdy z ![]()
wyrobów może być w całości wytworzony na każdym z ![]()
urządzeń.
Znane są:
a) macierz wydajności urządzeń
,
której element ![]()
oznacza liczbę jednostek j-tego wyrobu produkowaną przez i-te urządzenie w jednostce czasu,
b) maksymalny czas pracy poszczególnych urządzeń w ustalonym okresie czasu, np. w ciągu doby,
minimalne ilości poszczególnych wyrobów, które powinien wyprodukować wytwórca,
d) macierz kosztów
,
której element ![]()
oznacza koszt produkcji jednostki j-tego wyrobu na i-tym urządzeniu w jednostce czasu.
Należy wskazać ile wyrobów każdego rodzaju powinno być produkowane na poszczególnych urządzeniach, aby zostały spełnione powyższe wymagania i koszt produkcji był minimalny.
Zad. 3.1. Zakład włókienniczy wytwarza na dwóch typach maszyn tkackich o różnej wydajności dwa rodzaje tkanin i . W poniższej tabeli przedstawiono wydajności tych maszyn w zależności od rodzaju tkaniny.
|
Ilość tkaniny (w 1000 m) na 1 godzinę pracy maszyn |
|
|
|
. |
|
|
|
|
|
|
Sumaryczny czas pracy maszyn typu wynosi co najwyżej 36 godzin na dobę, a maszyn typu 98 godzin na dobę. Ułóż optymalny plan produkcji, wiedząc, że popyt na tkaninę jest 3 razy większy niż na tkaninę , a zysk jednostkowy z tytułu ich produkcji wynosi:
4 zł za metr tkaniny oraz 5 zł za metr tkaniny .
Zagadnienie transportowe
![]()
dostawców posiada jednorodny towar odpowiednio w ilościach jednostek. Całą masę towarową należy przetransportować do ![]()
odbiorców, których zapotrzebowanie odpowiednio wynosi jednostek. Znana jest macierz
,
której element ![]()
oznacza koszt transportu jednostki towaru od i-tego dostawcy do j-tego odbiorcy. Należy wyznaczyć taką macierz
,
gdzie ![]()
oznacza liczbę jednostek towaru, którą należy przetransportować od i-tego dostawcy do j-tego odbiorcy, aby sumaryczny koszt transportu był najmniejszy.
Zad. 4.1 Trzech dostawców posiada jednorodny towar w ilości ![]()
, ![]()
, ![]()
jednostek. Całą masę towarową należy przetransportować do pięciu odbiorców , których zapotrzebowanie odpowiednio wynosi ![]()
, ![]()
, ![]()
, ![]()
, ![]()
. Koszty transportu jednostki towaru od poszczególnych dostawców do poszczególnych odbiorców są zestawione w poniższej macierzy
Wyznaczyć minimalny koszt transportu.
5. Zadania o optymalnym rozkroju
5.1. Minimalizacja odpadu
Tartak otrzymał zamówienie na wykonanie co najmniej 300 kompletów belek. Każdy komplet składa się z 7 belek o długości 0.7 m oraz 4 belek o długości 2.5 m. W jaki sposób powinny być cięte dłużyce o długości 5.2 m, aby odpad powstały w procesie cięcia był minimalny ?
5.2. Maksymalizacja liczby kompletów
Tartak dysponuje dwoma grupami kłód drewna. Pierwsza grupa składa się z 99 kłód o długości 6.6 m, druga z 60 kłód o długości 4.8 m. Jak należy pociąć te kłody, aby otrzymać maksymalną liczbę kompletów składających się z 2 belek o długości 2.2 m i jednej belki o długości 1.3 m ?
6. Ogólny problem plecakowy
Danych jest n rzeczy każda w nieograniczonej ilości sztuk. Rzecz (jedna sztuka) waży jednostek i ma wartość jednostek pieniężnych. Dana jest ponadto maksymalna pojemność plecaka, wynosząca W jednostek. Należy wyznaczyć liczby sztuk poszczególnych rzeczy , których całkowita waga nie przekracza W i których sumaryczna wartość jest największa spośród wszystkich wypełnień plecaka rzeczami o pojemności nie przekraczającej W.
Ogólny problem plecakowy jest modelem matematycznym rozmaitych zagadnień spotykanych w praktyce, np. załadowanie kontenera, pociągu, promu, samochodu, walizki.
Zad. 6.1. Rozwiązać ogólny problem plecakowy dla przykładu scharakteryzowanego tabelą
|
1 |
2 |
3 |
4 |
5 |
W |
|
6 |
2 |
5 |
7 |
8 |
|
|
6 |
1 |
3 |
2 |
4 |
15 |
Ogólny problem plecakowy można również rozwiązać za pomocą metody programowania dynamicznego. Twórcą metody programowania dynamicznego jest amerykański matematyk Richard Bellman. Metoda nakazuje podzielić cały proces postępowania na skończoną liczbę etapów: . Rozwiązanie optymalne konstruujemy w oparciu o zasadę optymalności Bellmana, która poleca, aby na każdym kroku podejmować najlepszą decyzję z uwzględnieniem stanu wynikającego z poprzednich decyzji.
7. Problem komiwojażera
Komiwojażer wyjeżdża z miasta nr ![]()
, odwiedza ![]()
innych niast i powraca do miasta nr ![]()
. Znana jest macierz
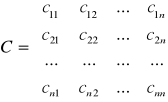
,
której element ![]()
oznacza odległość między miastami i-tym oraz j-tym. Zadanie polega na znalezieniu takiej kolejności odwiedzania miast, aby długość przebytej drogi była najmniejsza.
8. Optymalne przepływy w sieciach
8.1. Zagadnienie maksymalnego przepływu w sieciach
Zadana jest sieć transportowa (system rurociągów, system dróg kolejowych, system linii telekomunikacyjnych) za pomocą której chcemy przesłać jednorodny towar (ropa naftowa, pociągi, jednostki informacji) ze szczególnego punktu sieci zwanego węzłem startowym s do określonego punktu przeznaczenia zwanego węzłem docelowym d. Oprócz węzła źródłowego i docelowego sieć posiada skończoną liczbę węzłów pośrednich (tranzytowych). Węzły są połączone za pomocą łuków określających kierunek przepływu towaru. Węzły pośrednie mogą być interpretowane jako punkty przełączające lub punkty przeładunku towaru. Każdy łuk ![]()
(łączący węzeł i z węzłem j) posiada określoną przepustowość ![]()
. Jeśli przepływ ma się odbywać zarówno od węzła i do węzła j jak również od węzła j do węzła i, to w sieci węzły i, j łączymy dwoma łukami: ![]()
Przepływ towaru zapoczątkowany jest w węźle startowym s, przebiega wzdłuż łuków (tylko w nakazanym kierunku) poprzez węzły pośrednie do węzła docelowego d, aż towar, który rozpoczął podróż w węźle startowym zostanie w całości przetransportowany do węzła docelowego.
Zadanie polega na wyznaczeniu maksymalnego przepływu sieci, czyli ilości towaru, którą można przesłać z węzła s do węzła d.
Powyższy model może zostać uogólniony na kilka sposobów. Na przykład, sieć posiadającą kilka węzłów startowych można przekształcić w sieć o jednym źródle . Podobnie sieć o wielu węzłach docelowych można również przekształcić w sieć o jednym węźle docelowym . Z innym wariantem zagadnienia spotykamy się, gdy oprócz przepustowości łuków, dane są również zasobności węzłów. Te ostatnie mogą na przykład przedstawiać maksymalną ilość towaru, która może być przechowywana w węźle.
Do rozwiązania powyższego zagadnienia stosuje się w praktyce algorytm opracowany przez L. R. Forda i D. R. Fulkersona, zwany algorytmem przepłuwu maksymalnego. Należy on do kategorii algorytmów cechowania. Polega on na kolejnym przypisywaniu węzłom j cech postaci ![]()
lub ![]()
, gdzie
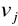
jest liczbą dodatnią, oznaczającą zmianę przepływu między węzłem j i poprzednim węzłem i;i+ oznacza przepływ
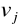
jednostek z węzła i do węzła j, natomiast i− oznacza przepływ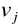
jednostek z węzła j do węzła i.
Algorytm maksymalnego przepływu
Krok 1. Znaleźć początkowe rozwiązanie dopuszczalne dla sieci. Możemy na przykład rozpocząć ze wszystkimi ![]()
.
Krok 2. Rozpocząć od węzła startowego i nadać mu cechę ![]()
. Oznaczenie to wskazuje, że w węźle źródłowym jest dostępna nieograniczona ilość towaru do przesłania.
Krok 3. Wybrać dowolny nie ocechowany węzeł i (początkowo cechę ma tylko węzeł źródłowy).
Krok 3a. Dowolnemu nie ocechowanemu węzłowi j, dla którego ![]()
, przypisać cechę ![]()
, gdzie ![]()
.
Krok 3b. Wszystkim węzłom j, które nie są ocechowanie i takie, że ![]()
, przypisujemy cechę ![]()
, gdzie ![]()
.
Gdy węzeł j otrzyma cechę, poddaje się go procesowi kroku 3 dopóki, dopóty wszystkie węzły ocechowane nie zostaną sprawdzone z węzłami nie ocechowanymi łączącymi je. Proces ten
albo doprowadza do do utworzenia drogi do węzła docelowego, który wtedy otrzymuje cechę (przechodzimy wówczas do kroku 4 algorytmu);
albo nie możemy znaleźć takiej drogi, która prowadzi do węzła docelowego (przechodzimy wówczas do kroku 5 algorytmu).
Krok 4. Węzeł docelowy otrzmuje cechę ![]()
(przy czym ![]()
oraz ![]()
na podstawie reguły wyboru dla ![]()
). Wyznaczamy nowe rozwiązanie dopuszczalne zgodnie ze wzorami:
![]()
dla ![]()
zawartego w drodze, gdy j ma cechę ![]()
;
![]()
dla ![]()
zawartego w drodze, gdy j ma cechę ![]()
;
![]()
dla ![]()
nie występujacego w drodze.
Następnie należy usunąć cechy i powtórzyć proces rozpoczynając krok 2 z nowym przepływem dopuszczalnym ![]()
.
Krok 5. Proces kończy się w momencie, gdy nie możemy znaleźć drogi z węzła startowego do węzła docelowego. Maksymalny przepływ f jest równy sumie wszystkich ![]()
utworzonych przez stosowanie kroku 3 (zakładając początkowe rozwiązanie dopuszczalne składajace się ze wszystkich ![]()
).
8.2. Zagadnienie przepływów sieciowych o minimalnym koszcie
Podobnie jak w zagadnieniu maksymalnego przepływu, mamy zadaną sieć przepływu, którą należy przesłać zadaną liczbę F jednostek jednorodnego towaru z węzła startowego s do węzła docelowego d. Z każdym łukiem ![]()
związany jest koszt ![]()
przesłania jednostki towaru z węzła i do węzła j. Zakładamy ponadto, że przepustowość każdego łuku ![]()
jest ograniczona z dołu liczbą ![]()
oraz z góry liczbą ![]()
Zadaną ilość towaru F należy przesłać z węzła s do węzła d w taki sposób, aby całkowity koszt transportu był minimalny.
Najogólniejszy algorytm sieciowy rozwiązania zadania przepływów sieciowych o minimalnym koszcie został opracowany przez D. R. Fulkersona i zwany jest algorytmem zepsutym.
9. Gry z naturą
Gry z naturą są grami dwuosobowymi o sumie zero, w których przeciwnik (natura) nie podejmuje decyzji w trakcie gry.
Przykład 1. Rolnik ma wybrać jeden z trzech możliwych terminów t1, t2, t3 zasiewu zbóż. Wielkość plonów z hektara zależy od terminu zasiewu i stanu pogody. Zostały one zestawione w poniższej tabeli (w której wyróżniono 4 stany pogody S1, S2, S3, S4).
Terminy |
Stany pogody |
|||
zasiewów |
S1 |
S2 |
S3 |
S4 |
t1 |
21 |
15 |
32 |
16 |
t2 |
28 |
20 |
10 |
20 |
t3 |
13 |
27 |
25 |
15 |
Należy wspomóc rolnika w podjęciu decyzji o wyborze terminu zasiewu zbóż.
Wyboru można dokonać w oparciu o jedno z poniższych kryteriów.
Kryterium Walda
Zakładamy, że zajdą warunki najbardziej niekorzystne dla podejmującego decyzję. Dlatego optymalna decyzja i jest wybierana według reguły minmax. Odnośnie przykładu 1:
Następnie wybieramy
.
Ostatecznie wybieramy termin pierwszy (t1) gwarantując sobie wydajność z hektara co najmniej 15 kwintali.
Kryterium Hurwicza
Określa się arbitralnie współczynnik ostrożności a następnie wybiera się strategię i, dla której największa jest wartość
Przyjmując w przykładzie 1 kolejno mamy:
Następnie wybieramy
.
Ostatecznie wybieramy termin pierwszy (t1) spodziewając się osiągnięcia wydajności 18.4 kwintali z hektara..
Kryterium Bayesa
Zakładamy, że wszystkie stany z natury są jednakowo prawdopodobne. Zatem najlepszą strategią jest ta strategia i, która daje największą średnią arytmetyczną wygranych, tzn.
.
Dla przykładu 1 mamy
Następnie wybieramy
.
Ostatecznie wybieramy termin pierwszy (t1) oczekując wydajności 21.0 kwintali z hektara..
10. Zadania rachunkowe
Zad. 1. Znaleźć maksimum funkcji
![]()
na zbiorze ograniczonym nierównościami
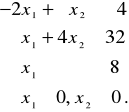
Zad. 2. Znaleźć minimum funkcji
![]()
na zbiorze ograniczonym nierównościami
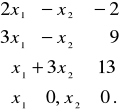
Zad. 3. Znaleźć maksimum funkcji
![]()
na zbiorze ograniczonym nierównościami
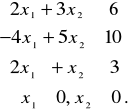
Zad. 4. Znaleźć maksimum funkcji
![]()
na zbiorze ograniczonym nierównościami
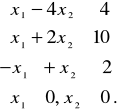
Zad. 5. Znaleźć minimum funkcji
![]()
na zbiorze ograniczonym nierównościami
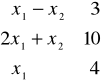
Praca pochodzi z serwisu www.e-sciagi.pl
1
2
Wyszukiwarka
Podobne podstrony:
Systemy operacyjne - wykłady, Administracja, Administracja, Administracja i samorząd, Polityka spole
wprowadzenie do sztucznej inteligencji-wyk łady (10 str), Administracja, Administracja, Administracj
podstawy projektowania w C++ - wykład, Administracja, Administracja, Administracja i samorząd, Polit
Forma wykorzystywanej informacji zewnetrznej, Administracja, Administracja, Administracja i samorząd
Wykladp, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna, informatyka
sciaga z C, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna, informatyka
informatyka - ściąga1, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna, i
Egzamin z informatyki, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna, i
projektowanie systemów informacyjnych (6 str), Administracja, Administracja, Administracja i samorzą
projektowanie systemów informacyjnych-ściąga, Administracja, Administracja, Administracja i samorząd
Sciaga z Sieci Komputerowych, Administracja, Administracja, Administracja i samorząd, Polityka spole
projektowanie systemów (17 str), Administracja, Administracja, Administracja i samorząd, Polityka sp
baza danych sciaga, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna, info
Informatyka-zagadnienia, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna,
projekt sieci komputerowej (9 str), Administracja, Administracja, Administracja i samorząd, Polityka
Telepraca1, Administracja, Administracja, Administracja i samorząd, Polityka spoleczna, Ochrona srod
więcej podobnych podstron