W 1797 Volta stwierdził, że przy zetknięciu ze sobą dwóch różnych metali powstaje między nimi różnica potencjałów. Na tej podstawie tak uszeregował metale, że każdy metal w szeregu przy zetknięciu z którymś z następnych, elektryzował się dodatnio. Powstająca różnica potencjałów na styku dwóch różnych metali nosi nazwę kontaktowej różnicy potencjałów.

W roku 1921 Seebeck wykazał, że jeżeli w zamkniętym obwodzie, składającym się z dwóch różnych metali, miejsca ich styków znajdują się w różnych temperaturach, to w obwodzie takim następuje przepływ prądu elektrycznego. Układ taki nazywamy termoogniwem.

Aby zrozumieć przyczynę która spowodowała powstanie różnicy potencjałów na styku różnych metali, należy rozpatrzyć stosunki energetyczne elektronów w poszczególnych metalach. Swobodne elektrony w metalu podlegają chaotycznym ruchom cieplnym i dzięki temu mogą się przemieszczać między węzłami sieci krystalicznej. Każdy z dodatnich jonów sieci oddziałuje na elektron swobodny, w wyniku czego uzyskuje on energię potencjalną odwrotnie proporcjonalną do wzajemnej odległości
.

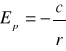
gdzie c- stała

Znak minus wynika z umowy. Teoria kwantowa podaje, że całkowita energia elektronu w atomie w obszarze „ujemnych” energii ( E<0 ) może przyjmować jedną z następujących wartości:
gdzie: B- stała dodatnia; n- główna liczba kwantowa przyjmująca wartości 1,2,3,...

Wynika z tego, że elektron w danych warunkach termodynamicznych może znajdować się tylko na określonym poziomie energetycznym. Rozkład poziomów energetycznych w polu kolumbowskiego oddziaływania jądra przedstawia rysunek.

Podobnie w kryształach elektrony walencyjne mogą znajdować się tylko na określonych poziomach energetycznych. Rozkład poziomów energetycznych w krysztale przedstawia rysunek.

W przestrzeni pomiędzy jonami krzywa energii potencjalnej przebiega płasko, jedynie w pobliżu jonów tworzą się wąskie i głębokie spadki (doły) potencjału. Obszar tych dołów potencjału jest mały w porównaniu z pozostałym obszarem kryształu, gdzie energia potencjalna nie zmienia się w sposób wyraźny. Można w dużym przybliżeniu przyjąć, że wewnątrz kryształu (metalu) energia potencjalna elektronów swobodnych ma wartość stałą równą
.

Rozmieszczenie elektronów swobodnych na poziomach energetycznych musi być zgodne z zasadą Pauliego. W myśl tej zasady na jednym poziomie energetycznym (jeżeli nie jest zdegenerowany) nie może być dwóch elektronów o takich samych liczbach kwantowych, muszą różnić się co najmniej kierunkiem własnych momentów magnetycznych (spinem). W temperaturze zera bezwzględnego T= 0 elektrony zapełniają najniższe poziomy energetyczne. Najwyższy z zajętych poziomów w T= 0 określa energię Fermiego
- poziom Fermiego.

W temperaturach pokojowych niektóre elektrony (bardzo mały procent) mają energię większą od energii Fermiego
i zajmują tym samym poziomy wyższe. Energia potencjalna elektronów wewnątrz kryształu (metalu) jest niższa niż na zewnątrz, dlatego elektrony nie są w stanie go opuścić.

Aby elektrony mogły opuścić metal i przesunąć się do tzw. próżni
, czyli miejsca, w którym nie dostrzega się praktycznie oddziaływań należy dostarczać energii z zewnątrz. Minimum energii potrzebnej elektronom do wyjścia z metalu równa się różnicy energii
i nazywa się pracą wyjścia. Ze względu na małe wartości prac wyjścia w porównaniu z jednostką energii w układzie SI- dżulem-mierzy się je w jednostkach mniejszych, zwanych elektronowoltami (eV). Jeden elektronowolt jest równy energii, jaką uzyska elektron przebywając różnicę potencjałów 1V.

Praca wyjścia określa wielkość potencjału, jaki uzyska elektron po opuszczeniu metalu i przejścia do „próżni”.

Praca wyjścia dla czystych metali waha się w granicach kilku elektronowoltów, np. dla cezu- 1,81 eV, platyny- 6,27 eV, wolframu- 4,52 eV, miedzi- 4,1 eV, srebra 4,7 eV.

Rozkład elektronów na poziomach energetycznych w metalu, w zależności od ich energii, przedstawia rysunek. Linia ciągła ilustruje rozkład energetyczny elektronów w T= 0, linia przerywana- ten sam rozkład w temperaturze T > 0.

Podczas zetknięcia się ze sobą dwóch różnych metali elektrony zaczną przechodzić z metalu, w którym ich energia jest większa ( mniejszy potencjał ) i będą go ładować ujemnie. Przechodzenie będzie trwało tak długo, aż wyrówna się energia całkowita elektronów walencyjnych. Warunkiem równowagi dynamicznej na styku jest równość energii elektronów swobodnych w obu metalach- odpowiada to zrównaniu poziomów Fermiego, w obu metalach. Zrównanie się poziomów Fermiego odpowiada sytuacji, gdy metal oddający elektron uzyskuje potencjał wyższy, przyjmujący elektrony- potencjał niższy. Wytworzyła się w ten sposób na styku metalu różnica potencjałów (napięcie kontaktowe). Powstałej różnicy potencjałów towarzyszy pole elektryczne skierowane do metalu, który uzyskał mniejszy potencjał. Pole to hamuje dalszy przepływ elektronów.

Rozpatrzymy od czego zależy wartość kontaktowej różnicy potencjałów na styku dwóch metali. Weźmy dwa metale A i B spojone i załóżmy, że praca wyjścia
elektronów z metalu B jest większa od pracy wyjścia
elektronów z metalu A. Na podstawie wzoru można napisać:

. Z założenia wynika nierówność:
<

W związku z tym elektrony zaczną przechodzić z metalu A do metalu B, tak długo, aż dojdzie do zrównoważenia się ich energii. Powstała różnica potencjałów w stanie równowagi będzie równa

Uwzględniają wzór, otrzymujemy wyrażenie na różnicę potencjałów na styku dwóch różnych metali, która wynika z różnicy ich prac wyjścia.

Drugim czynnikiem wpływającym na wartość kontaktowej różnicy potencjałów jest różna koncentracja elektronów swobodnych w obu metalach. Jeżeli przyjąć, że jednostkę objętości metalu A przypada
elektronów swobodnych, w metalu zaś B liczba ta wynosi
, to na styku tych metali istnieje gradient koncentracji elektronów, w którego wyniku będzie następować przepływ elektronu z metalu o koncentracji większej do metalu o koncentracji mniejszej. Przepływowi temu odpowiada wzrastająca różnica potencjałów na styku, która zahamuje ten przepływ elektronów. Obliczenia prowadzą do wniosku, że różnica potencjałów
zależy od stosunku koncentracji elektronów swobodnych w obu metalach oraz temperatury T.

gdzie: k- stała Boltzmana

Po uwzględnieniu obu przyczyn otrzymuje się wyrażenie na kontaktową różnicę potencjału:

Jeżeli utworzyć zamknięty obwód z dwóch różnych metali A i B tak aby ich spojenia miały różne temperatury, to w obwodzie tym będzie płynąć prąd elektryczny, ponieważ potencjał na spojeniu o wyższej temperaturze będzie wyższy niż na spojeniu o niższej temperaturze. Powstaje zatem różnica potencjałów, czyli różne od zera napięcie.

Ponieważ
, między spojeniami a i b wytworzy się tzw. siła termoelektromtoryczna , pod której działaniem w obwodzie popłynie prąd, co wskaże włączony mierniki. Wartość siły termoelektromtorycznej będzie równa algebraicznej sumie napięć na obu spojeniach.

Podstawiamy za odpowiednie wartości
i
ze wzoru i otrzymujemy:

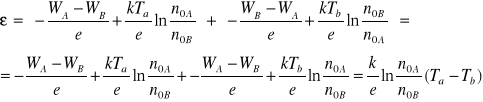
Podstawiamy za
. Można tak postąpić, ponieważ dobiera się dla danego zakresu temperatury taką parę metali, aby występujące w tym wzorze wielkości uznać za stałe. Ostateczne wyrażenie na siłę termoelektrodynamiczną można zapisać w postaci:

Z wyrażenia wynika, że siła termoelektromotoryczna jest wprost proporcjonalna do różnicy temperatur spojeń i zależy od rodzaju stykających się metali. We wzorze nie uwzględniono zmiany koncenetracji elektronów swobodnych w zależności od temperatury. Z tego względu dana para metali może być użyta do pomiaru temperatury tylko w tym zakresie, w którym stosunek koncentracji elektronoów można traktować jako stały.

Wartość siły termoelektromotorycznej dla temperatur metalicznych jest rzędu
. W celu zwiększenia czułości i uzyskana większych wartości siły termoelektromotorycznej stosuje się termopary próżniowe. Termopary można łączyć szeregowo ze sobą w celu zwiększenia wartości siły termoelektromotorycznej. Obecnie szerokie zastosowanie znalazły termopary wykonane z użyciem półprzewodników, które charakteryzują się znacznie większymi przyrostami siły termoelektromotorycznej przypadającej na jeden stopień ogrzania.

Termopary znalazły szerokie zastosowanie podczas pomiarów temperatury lub jako mikrochłodziarki, w których wykorzystuje się zjawisko Peltiera. Dzięki małej pojemności cieplnej termopar stosuje się je jako detektory słabego promieniowania. Połączone zaś w baterie mogą służyć jako źródła siły elektromotorycznej do zasilania układów tranzystorowych.

Zgodnie z prawem Ohma, siłę termoelektromotoryczną można wyrazić następującym wzorem:
gdzie: i- natężenie prądu termoelektrycznego; R- opór przyrządu pomiarowego (miliamperomierza); r- opór wewnętrzny termoogniwa (opór przewodników termoogniwa)

Porównując dwa wcześniejsze wzory otrzymamy związek pomiędzy natężeniem prądu danego termoogniwa a różnicą temperatur jego spojeń:

czyli:
lub
gdzie:

Ze wzoru wynika, że natężenie termoprądu jest wprost proporcjonalne do różnicy temperatury spojeń. Wniosek ten można zapisać w postaci następującej funkcji
. cechowanie sprowadza się do otrzymania na drodze doświadczalnej danych do jej wykreślenia. Wykresem funkcji
jest linia prosta.

---