EKSTREMA FUNKCJI PRZY WARUNKACH OGRANICZAJĄCYCH RÓWNOŚCIOWYCH WARUNKI KONIECZNE ISTNIENIA EKSTREMUM

Minimum warunkowe funkcji f(x) może istnieć tylko wówczas gdy nie istnieje żaden taki kierunek, w którym możemy dokonać nieskończenie małego przesunięcia i który należy do sektora kierunku spadku wartości funkcji f(x).

Jeżeli funkcje f(x) i g(x) są różniczkowalne w punkcie
i funkcje f(x) osiąga w tym punkcie ekstremum warunkowe przy warunku ograniczającym g(x)=0 to istnieje taka liczba
że zachodzi równość

oraz

i = 1,2,..., I

Metoda mnożników Lagrange'a

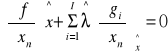
n= 1,2,...,N

warunki Lagrange'a

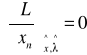
n = 1,2,...,N

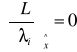
i = 1,2,...,I

EKSTREMA FUNKCJI PRZY WARUNKACH OGRANICZAJĄCYCH NIERÓWNOŚCIOWYCH

Jeżeli funkcje f(x), h_j(x) j=1,2,...,J przy czym x ∈ R_N, są różniczkowalne w punkcie
będącym punktem regularnym i funkcja f(x) osiąga w tym punkcie minimum warunkowe przy warunkach ograniczających h_j(x)=<0

J=1,2,...,J to są spełnione warunki.

Warunki Kuhna - Tuckera

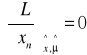
n=1,2,...,N

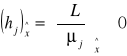
j=1,2,...,J

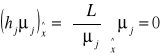
WARUNKI KONIECZNE ISTNIENIA MINIMUM FUNKCJI PRZY NIEUJEMNOŚCI JEJ ARGUMENTÓW

n=1,2,...,N

warunki Kuhna - Tuckera



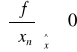
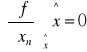
 n=1,2,...,N



OGÓLNE SFORMUŁOWANIE WARUNKÓW ISTNIENIA MINIMUM FUNKCJI PRZY WARUNKACH OGRANICZAJĄCYCH

i=1,2,...,I

j=1,2,...,J Kuhna - Tuckera

n=1,2,...,N'



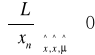
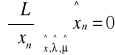
 n=1,2,...,N'



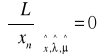
n=N'+1,...,N

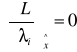
i=1,2,..,I

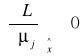
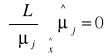
j=1,2,...,J

METODY NUMERYCZNE ZNAJDOWANIA PUNKTU MINIMUM FUNKCJI

Metoda gradientowa

Algorytm znajdowania miejsca zerowego funkcji

x (k+1) = x (k) - α_kp [ x (k) ]

p - funkcja dla której szukamy miejsca zerowego

α_k>0

1.

,

2.

,

Algorytm pochodnych

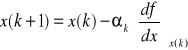
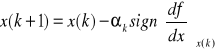
sign (u) = -1 jeżeli u < 0

0 jeżeli u = 0

1 jeżeli u > 0

Algorytm NEWTONA

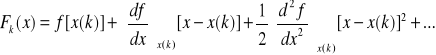
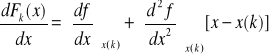
dla x = x ( k + 1 )

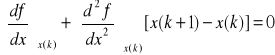
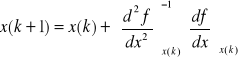
Algorytm złotego podziału (algorytm bez gradientowy)

Kurna nima

PODSTAWOWE METODY ZNAJDOWANIA MINIMUM FUNKCJI WIELU ZMIENNYCH

ALGORYTM GRADIENTOWY

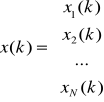
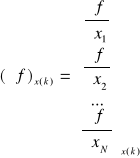
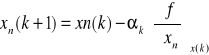
n=1,2,...,N

Algorytm NEWTONA

METODA FUNKCJI KARY

j=1,2,...,J

funkcja krytyczna f(x)

zmodyfikowana funkcja krytyczna

funkcja kary

blebleble

Metoda wewnętrznej funkcji kary

j=1,2,...,J

Metoda zewnętrznej funkcji kary

j=1,2,...,J

Metoda mieszanej funkcji

j=1,2,...,J₁ - powinny być spełnione

(wew. funkcje kary)

j=J₁+1,...,J - (zew. funkcje kary)

• ⇓

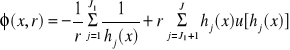
B(x) K(x)