Całki krzywoliniowe
Obliczyć całki nieskierowane
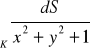
, gdzie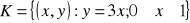
.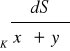
, gdzie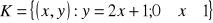
.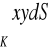
, gdzie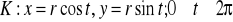
.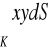
, gdzie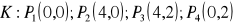
.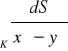
gdzie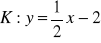
, odcinkiem AB :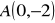
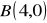
. (odp.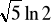
)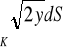
, gdzie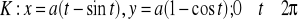
. (odp.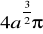
)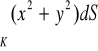
, gdzie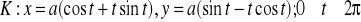
.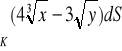
, gdzie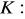
odcinek między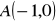
i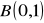
.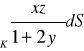
, gdzie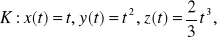
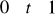
.
Obliczyć całki skierowane
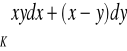
, gdzie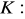
odcinek o początku w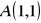
i końcu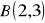
. (odp.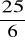
)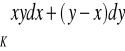
, gdzie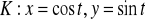
- okrąg zorientowany zgodnie ze wskazówkami zegara. (odp.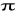
)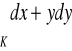
, gdzie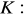
łuk paraboli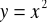
od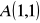
do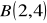
. (odp.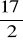
)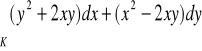
, gdzie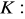
łuk paraboli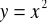
od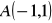
do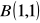
.
(odp. ![]()
)
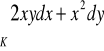
, gdzie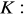
łuk paraboli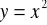
od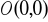
do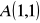
. (odp.1)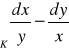
, gdzie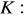
obwód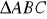
o wierzchołkach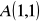
,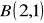
,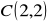
. (odp.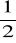
)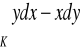
, gdzie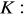
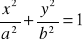
- dodatnio skierowana elipsa. (odp.
)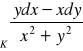
, gdzie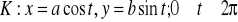
- dodatnio skierowana (odp.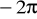
)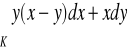
, gdzie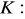
łuk paraboli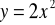
od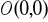
do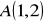
. (odp.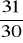
)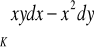
, gdzie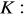
zorientowanym dodatnio łukiem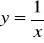
,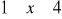
.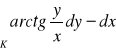
, gdzie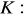
łuk paraboli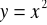
,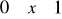
skierowany przeciwnie do wzrostu zmiennej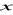
.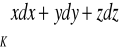
, gdzie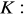
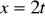
,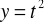
,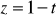
,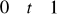
, skierowana zgodnie ze wzrostem parametru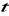
.
Zadania, w których można zastosować tw.Greena:
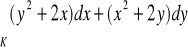
, gdzie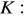
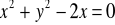
dodatnio skierowany. (odp.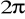
)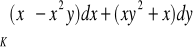
, gdzie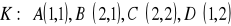
. (
) (odp.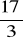
)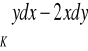
, gdzie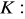
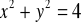
dodatnio skierowany. (odp.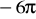
)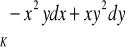
, gdzie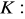
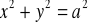
dodatnio skierowany. (odp.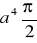
)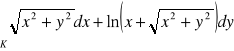
, gdzie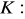
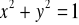
dodatnio skierowany. (odp.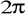
)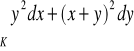
, gdzie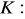
zorientowany dodatnio brzeg trójkąta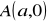
,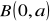
,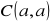
.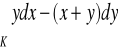
, gdzie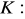
krzywa zamknięta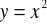
,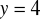
zorientowana dodatnio.
Sprawdzić, czy wyrażenie jest różniczką zupełną pewnej funkcji ![]()
- jeżeli tak, to wyznaczyć tą funkcję:
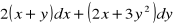
(odp.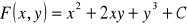
)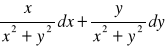
(odp.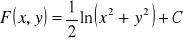
)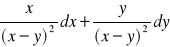
(odp.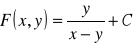
)
Obliczyć całki krzywoliniowe wzdłuż dowolnej krzywej:
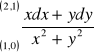
(odp.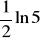
)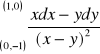
(odp.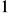
)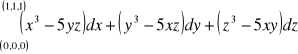
(odp.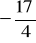
)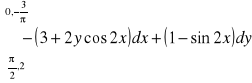
Wyszukiwarka
Podobne podstrony:
Zadania.Calki powierzchniowe, Oceanotechnika. PG, Semestr 2
Studia Niestacjonarne ZADANIA Z GEOMETRII WYKRESLNEJ, Mechanika i Budowa Maszyn PG, semestr1, Grafik
Zadanie 1 kolokwium 1 2007-08, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
Całki krzywoliniowe i powierzchniowe, Mechatronika WAT, Matma, Inne notatki zadania itp
Zadaniasiecdlastudentow, Budownictwo PG, Semestr 5, TiORB, ćwiczenia
Zadanie 3 kolokwium 1 rok2012-13, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kó
Zadanie 2 kolokwium 2 2010-11, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
Egzamin poprawkowy z matematyki rok 2010-2011 zadanie nr 4, Budownictwo PG, Semestr 3, Matematyka, P
Zadanie 5 kolokwium 1 2008-09, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
Zadanie 4 kolokwium 1 2011-12, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
zadania z relatywistyki, Budownictwo PG, Semestr 1, Fizyka, Ściągi, teoria na koła, Zadania, Relatyw
calki+krzywoliniowe, I semstr moje materiały, Matematyka 1 Semsetr, analiza mat zadania
LISTA 14 Całki krzywoliniowe
Zadania-lista4, POLITECHNIKA WROCŁAWSKA (2009), Semestr II, Fizyka 2
w 1 - wartość pieniądza w czasie - zadania dodatkowe, wszop ZZIP, II semestr, finanse i rachunkowość
Temat3, Mechanika i Budowa Maszyn PG, semestr 2, Materiałoznawstwo II, laborki
elektrotech test zeszly rok + zadanie na ten test, Uczelnia, semestr2, elektronika
zadania na kolokwium informatyka, gik, semestr 4, informatyka
więcej podobnych podstron