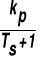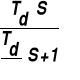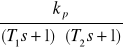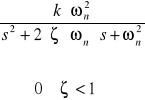Ćwiczenie nr 2

IDENTYFIKACJA OBIEKTU DYNAMICZNEGO

Laboratorium Automatyki i Sterowania

Zakład Energoelektroniki i Sterowania

1. Cel ćwiczenia.

Celem ćwiczenia jest badanie i identyfikacja podstawowych członów

dynamicznych. Zapoznanie się z opisem układów dynamicznych za pomocą równań macierzowych (tzn. równania stanu i równania wyjścia).

2. Wiadomości ogólne.

Układem dynamicznym nazywamy dowolny układ fizyczny rozpatrywany z punktu widzenia jego zachowania się w czasie, a więc z punktu widzenia zachodzących w nim procesów dynamicznych.

Nośnikami informacji o stanie układu są sygnały wychodzące z układu, którymi są przebiegi wielkości fizycznych(podlegających pomiarom), takich jak: prąd, napięcie, ciśnienie, położenie, temperatura, prędkość itd.

Wielkości te nazywamy sygnałami wyjściowymi, a miejsca w których je obserwujemy nazywamy wyjściami układu.

Czynniki zewnętrzne oddziałujące na układ są sygnałami wejściowymi (wymuszeniami), natomiast miejsca ich oddziaływania są wejściami układu.

Zbiór sygnałów wejściowych jest nazywany wektorem sygnałów wejściowych, a zbiór sygnałów wyjściowych wektorem sygnałów wyjściowych. Opis matematyczny takiego układu sprowadza się do związku między wektorem sygnałów wejściowych i wyjściowych. Może to być równanie różniczkowe, całkowe lub zależność operatorowa.

Układy w których związki między sygnałami wejściowymi a wyjściowymi mogą być przedstawione w postaci liniowych równań różniczkowych zwyczajnych o stałych parametrach nazywamy układami liniowymi stacjonarnymi o parametrach skupionych.

Dla układu liniowego stacjonarnego o parametrach skupionych odpowiedni jest opis w postaci następujących równań macierzowych, zwanych równaniami układu.

,

.

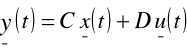
Związek między stanem układu x a sygnałem wejściowym u nosi nazwę równania stanu, zaś drugi związek wyrażający sygnał wyjściowy y przez kombinację liniową stanu układu i sygnału wejściowego - równania wyjścia.

Podstawową właściwością układów dynamicznych jest stabilność. W przypadku układu liniowego stacjonarnego wystarczy określić stabilność zwykłą i asymptotyczną.

Liniowy układ dynamiczny nazywamy stabilnym, jeżeli dla wszystkich (ograniczonych) stanów początkowych x
przy braku wymuszeń (zerowym sygnale wejściowym) sygnał wyjściowy pozostanie ograniczony, zaś asymptotycznie stabilnym, jeżeli również przy dowolnym ograniczonym sygnale wejściowym sygnał wyjściowy pozostaje ograniczony.

Dla liniowych układów dynamicznych wprowadza się pojęcie sterowalności i obserwowalności.

Układ sterowalny jest to układ, który stosując ograniczone, przedziałami ciągłe sterowanie można przeprowadzić z dowolnie zadanego stanu początkowego do początku układu współrzędnych przestrzeni stanów w skończonym czasie.

Pojęcie - układ obserwowalny oznacza, że przy dowolnie zadanym sterowaniu istnieje skończony przedział czasu taki, że na podstawie znajomości sterowanie i odpowiedzi w tym przedziale można wyznaczyć stan początkowy tego układu.

3. Układ ćwiczenia

Schemat płyty czołowej modelu laboratoryjnego przedstawiono poniżej. Struktura modelu odzwierciedla równania macierzowe(tzn. równania układu), przy wymiarach poszczególnych macierzy 2x2. Pozwala to na badanie liniowych układów dynamicznych do rzędu drugiego. Elementy macierzy A, B, C, D mogą przybierać wartości : A - od 0 do ± 7 ( wagi poszczególnych przycisków sumują się ), B - 0 lub 1, C - 0, +1, -1, D - 0 lub -1.

Całkowanie, zaznaczone schematycznie blokiem macierzy jednostkowej pomnożonej przez 1/s, może odbywać się w dwóch skalach czasu - naturalnej (1/sekundę) i przyspieszonej (100/sekundę). W drugim przypadku wartości elementów macierzy A i B należy pomnożyć przez 100.Przycisk ROZW.-CZAS START wyznacza chwilę t
, od której liczy się rozwiązanie.

Rys. 1. Schemat modelu badanego w ćwiczeniu

W położeniu spoczynkowym tego przycisku można ustawić warunki początkowe x
i x
współrzędnych stanu układu. Wartości współrzędnych stanu ( x
i x
) lub wyjścia ( y
i y
) można mierzyć na odpowiednich zaciskach lub orientacyjnie obserwować na wbudowanych wskaźnikach. Do układu można doprowadzić sygnały wymuszające ( sterujące ) po przez zaciski u
i u
; można również wprowadzić sygnały skokowe (stałe) o regulowanych amplitudach u
i u
wskazywane na miernikach, przy czym sygnały u
i u
oraz u
u
sumują się odpowiednio.

Do badania układu służy rejestrator o regulowanym przesuwie taśmy ok. 5 mm/s przy naturalnej skali modelu który należy połączyć z wyjściem y modelu. Przebiegi czasowe można również obserwować na oscyloskopie.

4. Podstawowe człony dynamiczne układu regulacji

Nazwa członu	Transmitancja operatorowa Rząd równania stanu	Charakterystyka skokowa
Bezinercyjny (proporcjonalny)	kp 0
Całkujący	1
Proporcjonalno - całkujący	1
Inercyjny	1
Różniczkujący rzeczywisty	1

Nazwa członu	Transmitancja operatorowa Rząd równania stanu	Charakterystyka skokowa
Człon całkujący z inercją	-----------------------------
Przesuwnik fazowy	1
Dwuinercyjny	2
Oscylacyjny	2

Schemat układu pomiarowego - pomiary

Nastawić należy za pomocą przycisków odpowiednie parametry macierzy w modelu tak aby uzyskać podstawowe człony: proporcjonalny, całkujący, inercyjny itd. Zarejestrować odpowiedzi tych członów na skok sygnału wejściowego a także na niezerowe warunki początkowe.

4. Sprawozdanie.

Sprawozdanie powinno zawierać:

1. schemat układu pomiarowego,

2. wyniki w postaci wykresów(na wykresach nanieść odpowiednio oś czasu oraz napięcia),

3. na podstawie otrzymanego wykresu oraz wartości macierzy przeanalizować otrzymane wyniki,

d) wyznaczyć wartości stałych czasowych, okresów oscylacji itd. dla zarejestrowanych przebiegów.

	B
1		1
1		1

		C
-1	+1		-1	+1
-1	+1		-1	+1

				A
+ -	1	2	4		+ -	1	2	4
+ -	1	2	4		+ -	1	2	4

	D
-1		-1
-1		-1

[ ]

Skala czasu

+

U + X + Y

+

---