LABORATORIUM Z MECHANIKI PŁYNÓW
Katedra Maszyn i Urządzeń Energetycznych.
Rok II Grupa 8	Imię i nazwisko: Hubert Wasilewski	Lab. wykonano: 10. 03. 1999.
Prowadzący lab.: dr inż.. T.Tokarz	Temat ćwiczenia nr 2: Wyznaczenie strat energii w przepływie płynu rzeczywistego.	Ocena:

I. Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie współczynnika oporów liniowych i współczynnika oporów miejscowych oraz strat energii w przepływie powietrza w rurociągu tłoczonym wentylatora promieniowego.

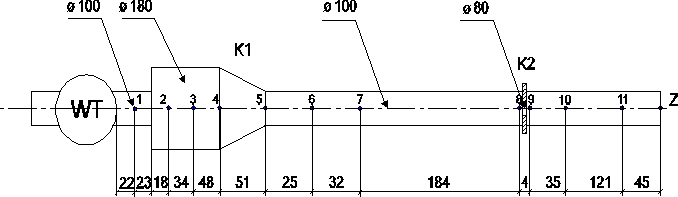
II. Schemat stanowiska pomiarowego.

WT - wentylator

K1 - konfuzor

K2 - kryza

Z - zasuwa

III. Wyniki pomiarów.

1. Dane stałe.

D₁ = 100 mm b = 737,2 mmHg

D₂ = 180 mm to = 20 ⁰C

kryza - d80/D100 ϕ = 65 %

ρ_Hg =13539 kg/m³

ρ_m = 825 kg/m³

2. Tabela wyników pomiarów.

Lp	Wielkość pomiarowa	Nr punktu pomiarowego 1 2 3 4 5 6 7 8 9 10 11
1	Ciśn.odniesienia ho [mm alk]	347,5	347,5	347,5	347,5	347,5	347,5	219,5	219,5	219,5	219,5	219,5
2	Ciśn. statyczne hi [mm alk]	166	163	144	142,5	232	216,5	95,5	100	334	202,5	225
3	Nadciśn. stat. hni [mm alk]	181,5	184,5	203,5	205	115,5	131	124	119,5	-114,5	17	-5,5
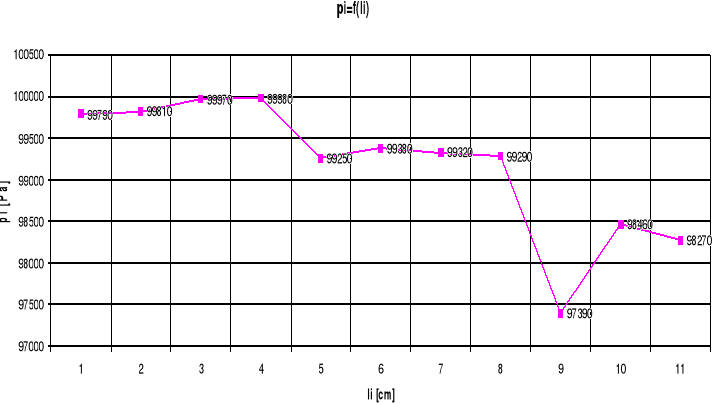
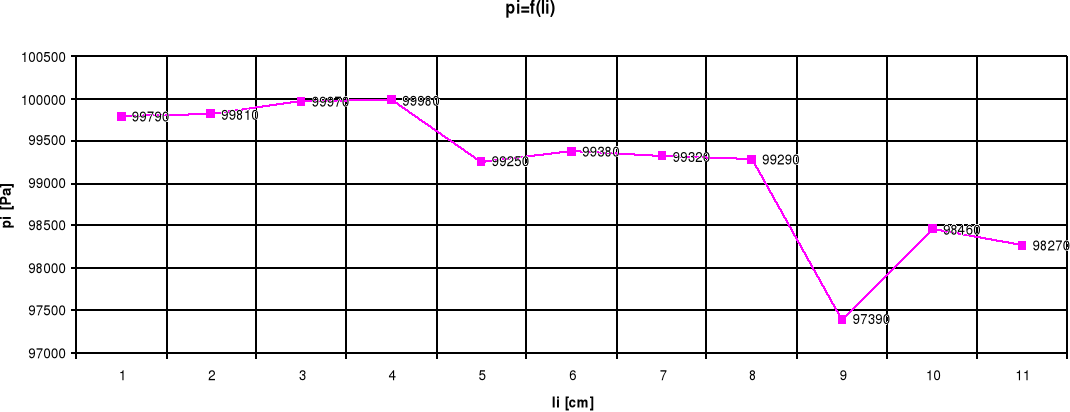
4	Bezwz. ciś. Stat. pi [Pa]	9,979*10^4	9,981*10^4	9,997*10^4	9,998*10^4	9,925*10^4	9,938*10^4	9,932*10^4	9,929*10^4	9,739 *10^4	9,846*10^4	9,827*10^4
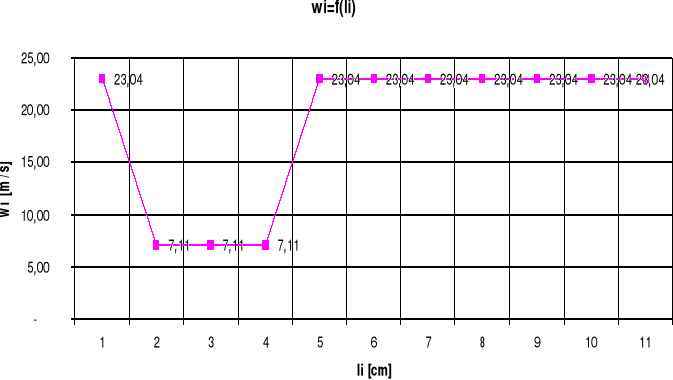
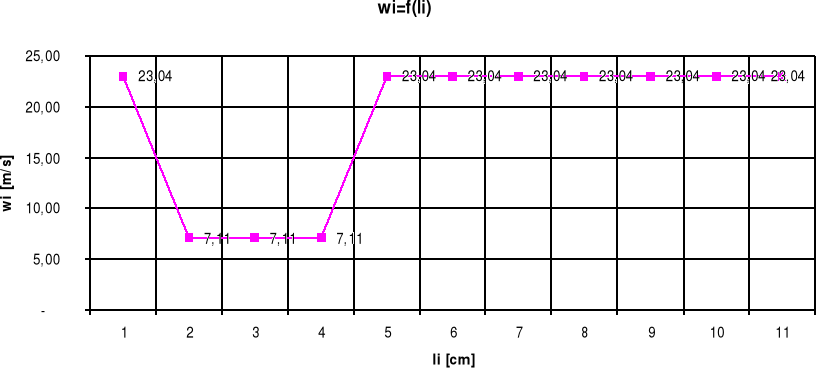
5	Prędk. Przepł. wi [m/s]	23,04	7,11	7,11	7,11	23,04	23,04	23,04	23,04	23,04	23,04	23,04

3. Wzory.

h_ni = h_o - h_i p_i = p_b + h_ni•ρ_m•g•10^-3 p_b = b•ρ_Hg•g•10^-3

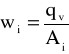
gdzie: w_i - prędkość średnia przepływu czynnika o strumieniu objętości q_v przez dany przekrój A_i

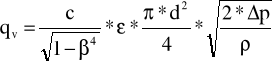
gdzie:

 - przewężenie zwężki pomiarowej,  = 0,75

p - ciśnienie różnicowe na zwężce, p = p₈ - p₉ = 9,929*10⁴ - 9,739*10⁴ = 1900 [Pa]

c - współczynnik przepływu (lepkość)

 - liczba ekspansji (ściśliwość)

ρ - gęstość powietrza,

ρn  , kg/m³ p8 = 9,929*10⁴

pn = 10⁵ Pa φ =0,65

Tn = 273,16 K pp'' = 2337 Pa

ρ''  , kg/m³

T = 293,16 K

ρ = 1,168 [kg / m³]

Zasada obliczania q_v wg PN na przykładzie badanego rurociągu:

1. Dla przyjętej wartości początkowej liczby Reynoldsa odczytuję z tablic wartość współczynnika przepływu dla danego rodzaju zwężki pomiarowej (c' = f (, Re')) Re' = 10⁶ dla kryzy ISA

z przytarczowym odbiorem ciśnienia i dla  = 0,75 - c' = 0,5959.

2. Obliczam wartość liczby ekspansji

gdzie:

χ - wykładnik adiabaty, χ=1,4

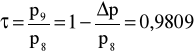
ε=0,9972

3.Obliczam przybliżenie q_v1

q_v1=

gdzie: d = 0,075 m

q_v1=

q_v1=0,17593[] (q_v=c`*0,30160)

4.Obliczam przybliżoną wartość prędkości średniej przepływu:

W_I=

dzie: Δ = d₈ = 0,1 m

w_I= (w=127,32336*q_v)

5.Określam rzeczywistą wartość liczby Reynoldsa:

Re_r=

gdzie:

po odczytaniu z tablic: μ=18*10^-6[Pa*s] dla

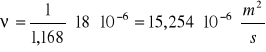
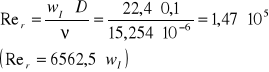
6.Określam rzeczywisty współczynnik przepływu:

c=f(β,Re_r) z tablic - c=0,6025(dla Re=10⁵) oraz dla tej wartości c strumień objętości i prędkości

q_vII=0,6025*0,30160=0,17787

w_II=127,32336*0,17787=22,647

stąd Re_r`=6562,5*w_II=1,486*10⁵ stąd określam kolejny raz współczynnik c, który przyjmuję za rzeczywisty: c=0,60025

/wartość c odczytywana z tablic (wg normy PN-93/M.-53950/01) została w tym przypadku uśredniona między wartością dla Re=10⁵ a Re=3*10⁵z powodu braku możliwości określenia dokładnego c/

7. Określam rzeczywistą wartość strumienia objętości

q_v= 0,30160*c

q_v=0,30160*0,60025=0,18098

8.Obliczam wartość prędkości średniej w poszczególnych punktach badanego rurociągu.

w_i=

wartość prędkości średniej umieszczono w tabeli.

9. Obliczenie strat liniowych.

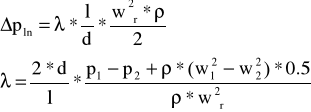
_1-2 = 0,489

_2-3 = -2,762

_3-4 = -0,151

_4-5 = 0,882

_5-6 = -0,161

_6-7 = 0.049

_7-8 = 0,614

_9-10 = -0,981

_10-11 = 0,048

Obliczone wartości współczynników strat liniowych nie pokrywają się z wartościami tablicowymi.

Dla dwóch najbardziej wiarygodnych wyników obliczam średnią arytmetyczną i dla jej wartości dokonuję obliczeń strat liniowych.

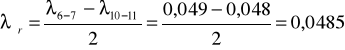
p_ln1-2 = 26,391

p_ln2-3 = 2,705

p_ln3-4 = 3,818

p_ln4-5 = 23,448

p_ln5-6 = 37,608

p_ln6-7 = 48,139

p_ln7-8 = 276,798

p_ln9-10 = 52,652

p_ln10-11 = 182,025

Całkowite straty liniowe wynoszą p_ln = p_lni = 653,574

gdzie:

i - ilość uwzględnionych odcinków.

10. Obliczenie strat miejscowych.

Występują one dla nagłego zwiększenia przekroju 1-2, zwężenia w punktach 4-5 i kryzy 8-9.

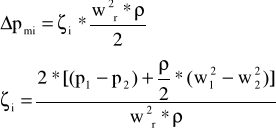
_1-2 = 1,933 p_{m 1-2} = 256,651

_4-5 = 2,398 p_{m 4-5} = 318,35

_8-9 = 6.087 p_{m 8-9} = 1888

Całkowite straty liniowe wynoszą p_m = 2463

gdzie: i - ilość uwzględnionych odcinków.

Całkowite straty wynoszą h_st = p_ln + p_m = 653,574 + 2463 = 3116,574

11. Obliczenie strat energii.

h_n = h_n-1 + p_ln +p_m

h₁ = 0

h₂ = 283,042

h₃ = 285,747

h₄ = 289,565

h₅ = 631,363

h₆ = 668,971

h₇ = 717,11

h₈ = 993,908

h₉ = 2881,908

h₁₀ = 2934,56

h₁₁ = 3116,585

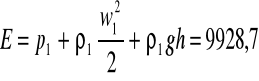
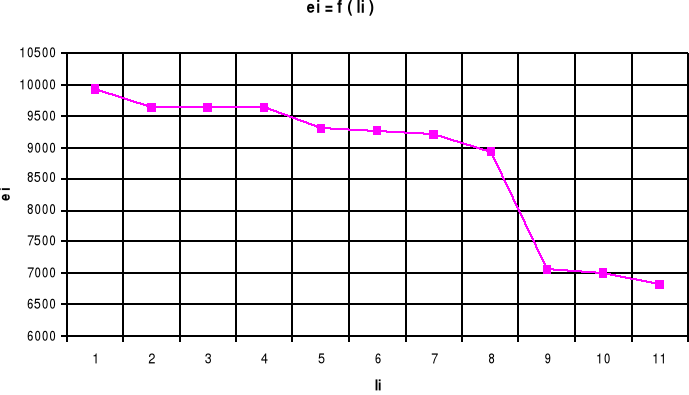
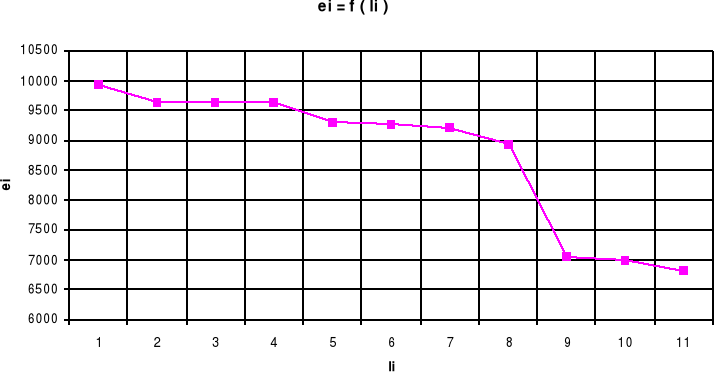
E_n = E - h_n

E₁ = E = 9928,7

E₂ = 9645,658

E₃ = 9642,953

E₄ = 9639,135

E₅ = 9297,337

E₆ = 9259,729

E₇ = 9211,59

E₈ = 8934,792

E₉ = 7046,792

E₁₀ = 6994,14

E₁₁ = 6812,115

Wykres strat energii w funkcji długości rurociągu.

---