LABORATORIUM Z FIZYKI.
Wydział Mechaniczny Grupa : 13a Zespół : 1 Nr ćwiczenia : O2
|
Krzysztof Dębski
Temat ćwiczenia: Wyznaczanie kąta skręcenia płaszczyzny polaryzacji i skręcenia właściwego r-ru cukru. |
|
Data: 14.04.1999 |
Ocena : |
Podpis : |
Wykonanie:
|
|
|
Światło jest poprzeczną falą elektromagnetyczną. Zazwyczaj światło jest falą bardzo złożoną ponieważ występują równocześnie fale o różnych długościach, a drgania zachodzą we wszystkich płaszczyznach przechodzących przez kierunek rozchodzenia się. Istnieje kilka metod polaryzacji światła:
przez podwójne załamanie,
przez odbicie lub wielokrotne załamanie,
przez dichroizm
W kryształach występuje zjawisko podwójnego załamania, w którym pojedyncza wiązka światła ulega rozszczepieniu na dwie wiązki, zwyczajną i nadzwyczajną. Substancje krystaliczne, dzięki prawidłowemu przestrzennemu rozmieszczeniu atomów przejawiają swoiste właściwości optyczne. Na ogół wektor świetlny E promienia światła nie ma całkowitej swobody wykonywania drgań wewnątrz kryształu lecz są mu narzucone tylko dwa prostopadłe do siebie kierunki drgań. Istnieje jednak we wnętrzu kryształu jednak kierunek, w którym to promień ma całkowitą swobodę wykonywania drgań. Jest to kierunek tzw. osi optycznej. Dzięki tej własności kryształów promień światła naturalnego padając na kryształ w kierunku niezgodnym z osią optyczną ulega podwójnemu załamaniu, to znaczy rozkłada się na dwa promienie spolaryzowane liniowo, drgające w płaszczyznach wzajemnie prostopadłych, a mianowicie na tzw. promień zwyczajny i promień nadzwyczajny. Uzyskanie światła spolaryzowanego liniowo sprowadza się do wyeliminowania jednego z promieni. Osiągnąć to można przez zastosowanie pryzmatu Nicola, lub przez wykorzystanie zjawiska dichroizmu. Pryzmat Nicola jest pryzmatem ze szpatu islandzkiego (CaCO3) występujący w naturze w postaci słupków równoległościennych, który to po odpowiednim oszlifowaniu jego podstaw i przecięciu wzdłuż płaszczyzny przekątnej, zostaje sklejony za pomocą balsamu kanadyjskiego. Współczynniki załamania n szpatu wynoszą: n=1.66 - dla promienia zwyczajnego oraz n=1.49 dla nadzwyczajnego, a współczynnik dla balsamu kanadyjskiego wynosi n=1.55. promień światła naturalnego wchodząc do pryzmatu ulega rozłożeniu na dwa promienie: zwyczajny i nadzwyczajny. Są one spolaryzowane liniowo, padają pod różnym kątem na warstwę balsamu. Dzięki odpowiednio dobranym kątom pryzmatu, promień nadzwyczajny pada pod kątem większym od kąta granicznego, ulega całkowitemu odbiciu wewnętrznemu, a następnie zostaje pochłonięty przez zaczernioną powierzchnię obudowy pryzmatu Nicola. W polaroidach do uzyskania światła spolaryzowanego wykorzystuje się tzw. zjawisko dichroizmu kryształów. Kryształy dichroniczne (np. turmalin ) wykazują różnicę współczynników pochłaniania promieni zwyczajnego i nadzwyczajnego. Można tak dobrać grubość warstwy krystalicznej, że po jej przejściu jeden z promieni ulega całkowitemu wygaszeniu. na drugą stronę warstwy przejdzie wówczas jedynie drugi promień, lecz o mniejszym natężeniu, ale spolaryzowany liniowo. Zjawisko to wykorzystywane jest przy wytwarzaniu cienkich warstewek polaryzujących liniowo światło.
Jeśli pomiędzy dwa skrzyżowane nikole polaroidy wstawimy płytkę z kwarcu wyciętą prostopadle do osi optycznej, to w świetle jednorodnym zauważymy rozjaśnienie pola widzenia. Rozjaśnienie to można usunąć obracając analizator o pewien kąt w lewo lub w prawo. Płytka kwarcowa spowodowała skręcenie płaszczyzny drgań lub płaszczyzny polaryzacji przechodzącego przez nią światła spolaryzowanego przez polaroid. Istnieje wiele ciał skręcających płaszczyznę polaryzacji. Nazywamy je ciałami optycznie czynnymi. Należą do nich ciała stałe, ciecze, gazy oraz roztwory niektórych substancji np. roztwór cukru.
Ciało optycznie czynne dzieli padającą wiązkę spolaryzowaną liniową na składową spolaryzowaną kołowo prawoskrętnie i kołowo lewoskrętnie. Zjawisko to nosi nazwę dwółomności kołowej. Polaryzacja kołowa oznacza takie uporządkowanie drgań, przy którym wektor świetlny E obraca się na około promienia światła. Jego koniec zakreśla linię śrubową. Obie składowe rozchodzą się z różnymi prędkościami, w wyniku czego wytwarza się między nimi różnica faz. Przy wyjściu z ciała obie składowe dodają się i wypadkowa, chociaż nadal spolaryzowana liniowo, ma już inny azymut polaryzacji. Jeśli znane są oba współczynniki załamania i długości przebytej przez światło w danym ośrodku drogi l, różnicę faz można obliczyć na podstawie wzoru:
![]()
gdzie:
n - różnica współczynników załamania,
λ - długość fali światła,
φ- kąt skręcenia stanowi połowę różnicy faz, ![]()
W przypadku roztworów okazuje się, iż kąt skręcania jest proporcjonalny do długości l warstwy roztworu oraz do jego stężenia c. Tę zależność wyraża wzór:
![]()
gdzie:
K - współczynnik proporcjonalności zależny od:
rodzaju rozpuszczonej substancji,
rodzaju rozpuszczalnika,
długości fali światła.
Przyrządem do pomiaru skręcania płaszczyzny polaryzacji światła w substancjach optycznie czynnych jest polarymetr. Polarymetry przeznaczone do pomiaru stężenia cukru nazywamy sacharymetrami.
Przebieg ćwiczenia.
Wykonywanie roztworów wodnych cukru (1,2,3,4,5 %) oraz obliczanie błędów stężeń tych roztworów.
Do obliczania stężeń roztworów wykorzystano wzór:
![]()
⇒ ![]()
c - stężenie roztworu
mc - masa cukru
mw - masa wody
Do obliczania błędów stężeń wykorzystano wzór:
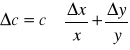
Δc - błąd stężenia
Δx - dokładność wagi
Δy - dokładność menzurki
x - masa użytego cukru
y - masa użytej wody
Przyjęto następującą dokładność przyrządów:
Δx = 0.002 g (dokładność wagi)
Δy = 0.5 g (dokładność menzurki)
Masę wody przyjęto: 20 g.
1) Roztwór 1%
![]()
![]()
![]()
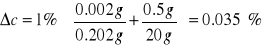
2) Roztwór 2%
![]()
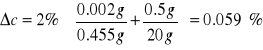
3) Roztwór 3%
![]()
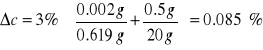
Roztwór 4%
![]()
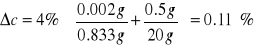
5) Roztwór 5%
![]()
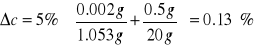
Średnia błędów stężeń wynosi:
![]()
Pomiary i rachunek błędów:
Woda destylowana:
L.P |
αo |
αo - αs |
(αo - αs)2 |
1 |
0.1 |
0.1 |
0.01 |
2 |
0.0 |
0.0 |
0.0 |
3 |
- 0.3 |
-0.3 |
0.09 |
4 |
0.0 |
0.0 |
0.0 |
5 |
0.2 |
0.2 |
0.04 |
|
αs = 0.0 |
|
|
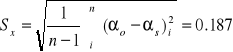
α = (0.0 +- 0.187)
Roztwór 1% cukru:
L.P |
αo |
αo - αs |
(αo - αs)2 |
1 |
1.5 |
0.02 |
0.0004 |
2 |
1.45 |
-0.03 |
0.0009 |
3 |
1.4 |
-0.08 |
0.0064 |
4 |
1.5 |
0.02 |
0.0004 |
5 |
1.55 |
0.07 |
0.0049 |
|
αs = 1.48 |
|
|
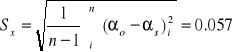
α = (1.48 +- 0.057)
Roztwór 2% cukru:
L.P |
αo |
αo - αs |
(αo - αs)2 |
1 |
3.0 |
-0.04 |
0.0016 |
2 |
3.05 |
0.01 |
0.0001 |
3 |
3.1 |
0.06 |
0.0036 |
4 |
3.0 |
-0.04 |
0.0016 |
5 |
3.05 |
0.01 |
0.0001 |
|
αs = 3.04 |
|
|
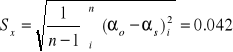
α = (3.04 +- 0.042)
Roztwór 3% cukru:
L.P |
αo |
αo - αs |
(αo - αs)2 |
1 |
4.4 |
0.04 |
0.0016 |
2 |
4.45 |
0.09 |
0.0081 |
3 |
4.25 |
-0.11 |
0.0121 |
4 |
4.3 |
-0.06 |
0.0036 |
5 |
4.4 |
0.04 |
0.0016 |
|
αs = 4.36 |
|
|
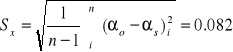
α = (4.36 +- 0.0822)
Roztwór 4% cukru:
L.P |
αo |
αo - αs |
(αo - αs)2 |
1 |
6.05 |
0.12 |
0.0144 |
2 |
6.0 |
0.07 |
0.0049 |
3 |
5.9 |
-0.03 |
0.0009 |
4 |
6.0 |
0.07 |
0.0049 |
5 |
5.7 |
-0.23 |
0.0529 |
|
αs = 5.93 |
|
|
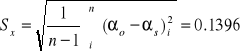
α = (5.93 +- 0.1396)
Roztwór 5% cukru:
L.P |
αo |
αo - αs |
(αo - αs)2 |
1 |
6.8 |
0.22 |
0.0484 |
2 |
6.7 |
0.12 |
0.0144 |
3 |
6.7 |
0.12 |
0.0144 |
4 |
6.4 |
0.18 |
0.0324 |
5 |
6.3 |
0.28 |
0.0784 |
|
αs = 6.58 |
|
|
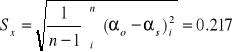
α = (6.58 +- 0.217)
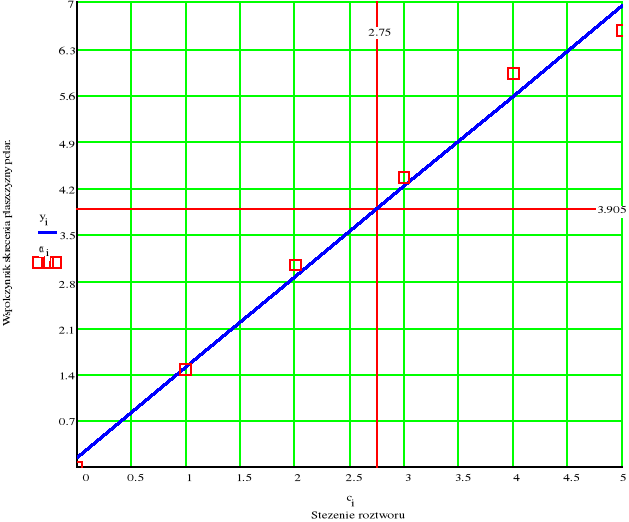
Wykres zależności kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu.
Prosta regresji:
![]()
Współczynniki prostej regresji:
![]()
![]()
Właściwa zdolność skręcająca cukru wynosi:
![]()
L.P |
[α] |
[α] - [αs] |
([α] - [αs])2 |
1 |
0.74 |
0.01 |
0.0001 |
2 |
0.76 |
0.03 |
0.0009 |
3 |
0.73 |
0.0 |
0.0 |
4 |
0.74 |
0.01 |
0.0001 |
5 |
0.66 |
-0.07 |
0.0049 |
|
[αs] = 0.73 |
|
|
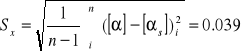
[α] = (0.73 +- 0.039)
dla dowolnego współczynnika αx = 3.905 obliczam nieznane stężenie roztworu:
![]()
![]()
porównując wartość obliczoną z wartością odczytaną z wykresu widać, że wartości te są prawie identyczne i mieszczą się w zakresie obliczonych błędów.
Wnioski:
Wraz ze wzrostem stężenia roztworu wzrasta kat skręcenia płaszczyzny polaryzacji.
Wyszukiwarka
Podobne podstrony:
FIZ O1, Inżynieria Środowiska PŚk, Semestr 2, Fizyka, Labo
O6, Inżynieria Środowiska PŚk, Semestr 2, Fizyka, Labo
cwiczenie O4, Inżynieria Środowiska PŚk, Semestr 2, Fizyka, Labo
Super sprawozdanie M7, Inżynieria Środowiska PŚk, Semestr 2, Fizyka, Labo
więcej podobnych podstron