2. Charakterystyki liczbowe

Analiza danych statystycznych polega na wyznaczeniu charakterystyk liczbowych badanych cech nazywanych parametrami statystycznymi.

Parametry dzieli się na:

• miary położenia,

• miary zmienności (dyspersji, rozrzutu, rozproszenia ),

• miary asymetrii (skośności),

• miary koncentracji.

1. Charakterystyki liczbowe
   -wzory dla danych indywidualnych

( danych nieuporządkowanych i szeregów szczegółowych.)

Niech x₁, x₂, … , x_n, 1 ≤ n ≤ 30 ( próba mała) będzie próbą losową pobraną z populacji.

1. Miary położenia

1. Średnia arytmetyczna

2. Moda (dominanta, wartość modalna)
   
   Moda jest to wartość cechy najczęściej powtarzającą się . Oznaczamy ją symbolami Mo lub D.

Interpretacja : Najliczniejszą grupę w populacji stanowią te osobniki, u których wartość badanej cechy jest równa Mo.

3. Mediana , Kwartyl II - Q_II, M_e

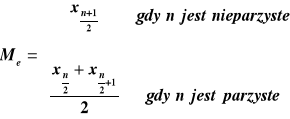
Mediana dzieli zbiorowość na dwie równe części. 50% jednostek populacji ma wartości cechy nie większe od M_e, a połowa jednostek wartości cechy
nie mniejsze od M_e .

2. Miary zmienności

Miary zmienności charakteryzują stopień zróżnicowania jednostek zbiorowości pod względem badanej cechy.

Parametry dzieli się następująco:

1. Wariancja

2. Odchylenie standardowe

Interpretacja:

Wartości cechy różnią się przeciętnie od wartości średniej arytmetycznej
o wartość odchylenia standardowego s.

3. Obszar wartości typowych

Około 70% jednostek ma wartość badanej cechy w przedziale
.

4. Współczynnik zmienności

Duże wartości współczynnika zmienności świadczą o dużym zróżnicowaniu wartości badanej cechy. Przyjmuje się, że jeśli współczynnik zmienności ma wartość mniejszą od 10%, zróżnicowanie cechy jest statystycznie nieistotne.

Współczynniki zmienności stosuje się zwykle do porównania zmienności cechy w kilku populacjach.

5. 
   Rozstęp cechy w próbie (charakteryzuje obszar zmienności badanej cechy)
   
   

1. Współczynnik asymetrii

Klasyczny współczynnik asymetrii

, s - odchylenie standardowe

Współczynnik asymetrii przyjmuje wartość z przedziału *-1 ; 1* , w przypadku skrajnej asymetrii może wykraczać poza ten przedział.

Określa on siłę i kierunek asymetrii.

M_o M_e

x

Asymetria lewostronna , A<0 Asymetria prawostronna , A>0

Im |A| jest bliższy 1 , tym asymetria jest silniejsza.

Dla rozkładu symetrycznego A=0.

2. Miara skupienia

Kurtoza (skupienie, koncentracja) - współczynnik określający koncentrację wartości cechy wokół wartości średniej.

,

s - odchylenie standardowe.

Im większa jest wartość współczynnika C, tym wykres funkcji gęstości cechy jest bardziej wysmukły, im mniejszy tym bardziej spłaszczony. Dla rozkładu normalnego C=0.

Krzywe częstości w populacjach o różnej koncentracji cechy

Dla
- skupienie mniejsze niż w rozkładzie normalnym.

Dla
- skupienie większe niż w rozkładzie normalnym.

Przykład 1

Ludność województw w milionach, stan w dniu 31.12.2006

	województwa	Ludność xi
	Lubuskie	1,0084	-1,3743	1,8888	-2,5958	3,5674
	Opolskie	1,0419	-1,3408	1,7978	-2,4106	3,2321
	Podlaskie	1,1961	-1,1866	1,4081	-1,6709	1,9827
	Świętokrzyskie	1,2798	-1,1029	1,2164	-1,3416	1,4797
	Warmińsko-mazurskie	1,4269	-0,9558	0,9136	-0,8732	0,8347
	Zachodniopomorskie	1,6929	-0,6898	0,4759	-0,3283	0,2264
	Kujawsko-pomorskie	2,0657	-0,3170	0,1005	-0,0319	0,0101
	Podkarpacki	2,0976	-0,2851	0,0813	-0,0232	0,0066
	lubelskie	2,1728	-0,2099	0,0441	-0,0093	0,0019
	Pomorskie	2,2036	-0,1791	0,0321	-0,0057	0,0010
	Łódzkie	2,5662	0,1835	0,0337	0,0062	0,0011
	Dolnośląskie	2,8815	0,4988	0,2488	0,1241	0,0619
	Małopolskie	3,2712	0,8885	0,7894	0,7014	0,6231
	Wielkopolskie	3,3783	0,9956	0,9912	0,9868	0,9824
	Śląskie	4,6692	2,2865	5,2280	11,9536	27,3316
	Mazowieckie	5,1715	2,7888	7,7773	21,6890	60,4859
Sumy		38,1236	X	23,0267	26,1707	100,8289

Miary położenia

1. 
   Średnia arytmetyczna

2. Moda

Wartości modalnej nie można wyznaczyć.

3. Mediana

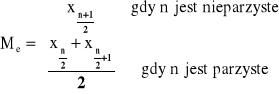
n=16 i jest liczbą parzystą,

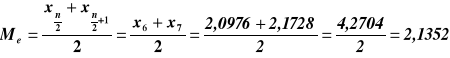
50% województw ma nie więcej niż 2,1352 mln ludności i 50% województw ma nie mniej niż 2,1352 mln ludności.

Miary zmienności

1. Wariancja

2. Odchylenie standardowe

Liczba ludności województw różni się przeciętnie od średniej o s=1,2 mln osób.

3. Obszar wartości typowych

2,383 - 1,2 < x_typ < 2,383 + 1,2

1,183 < x_typ < 3,583

5. Współczynnik zmienności

Współczynnik zmienności wskazuje na silne zróżnicowanie województw pod względem liczby mieszkańców

Województwa n=16	Ludność xi
Sumy	38,1236	X	23,0267	26,1707	100,8289

Klasyczny współczynnik asymetrii

, s - odchylenie standardowe

Wartość współczynnika A świadczy o silnej asymetrii prawostronnej.
Oznacza to, że , czyli więcej niż 50% województw ma liczbę mieszkańców mniejszą od średniej równej 2,383 mln.

Kurtoza

,

Współczynnik koncentracji jest równy 0 , co oznacza takie skoncentrowanie liczby mieszkańców województw wokół wartości średniej jak w rozkładzie normalnym.

14

Wykład 2 Statystyka i demografia, Administracja 9

pozycyjne

f(x)

Miary zmienności

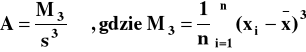
ω

ω

x M_e M_o

x

C>0

C=0

C<0

x

ω

sred	2,382725
s2	1,439172
s	1,199655
v	50,34802
typ	1,18307	3,58238
m3	1,635667		s^3	1,72651
a	0,947384
m4	6,301805		s^4	2,071216
c	3,042563		0,042563

Miary położenia

klasyczne

pozycyjne

kwartyle

średnia arytmetyczna

średnia harmoniczna

średnia geometryczna

modalna

rozstęp

odchylenie ćwiartkowe

współczynnik zmienności

wariancja

odchylenie standardowe

współczynnik zmienności i inne

klasyczne

kwartyl pierwszy

mediana (kwartyl drugi )

kwartyl trzeci

ω

x-ludność

M_e

_

x

50% lud.

50% lud.

>50% lud.

<50% lud.

---