1.Modele budowy atomu
Model Thomsona
W 1903 r. J.J. Thomson zaproponował następujący model atomu. Atom ma postać kuli równomiernie wypełnionej elektrycznym ładunkiem dodatnim, wewnątrz której znajduje się elektron. Sumaryczny ładunek dodatni kuli równy jest ładunkowi elektronu, tak więc atom jako całość jest obojętny elektrycznie.
Natężenie pola wewnątrz równomiernie naładowanej kuli opisane jest wyrażeniem
gdzie e - ładunek kuli, R - jej promień. Zatem na elektron, znajdujący się w odległości r od położenia równowagi (od środka kuli), będzie działać siła
e - ładunek elektronu, m - masa elektronu, R - promień atomu). Możemy posłużyć się tym związkiem do oszacowania wymiarów atomu. Zgodnie z powyższym wzorem
Długość fali l=6000 A (zakres widzialny widma) odpowiada w=3*1015 s-1. Zatem
Model Rutherforda
Rozkład dodatnich i ujemnych ładunków w atomie może być wyznaczony doświadczalnie za pomocą bezpośredniego "sondowania" wnętrza atomu. Takie sondowanie przeprowadził E. Rutherford razem ze współpracownikami za pomocą cząstek a; obserwowali oni zmianę kierunku ich lotu (rozproszenie) przy przechodzeniu przez cienka warstwę materii.
Przypomnijmy, że cząstkami a nazywamy cząstki emitowane przez niektóre substancje podczas rozpadu promieniotwórczego. Cząstki a mają prędkości rzędu 107 m/s. W momencie. gdy Rutherford przystępował do swoich doświadczeń, wiadomo było, że cząstka a ma ładunek dodatni równy podwojonemu ładunkowi elementarnemu i że tracąc ten ładunek (poprzez przyłączenie dwu elektronów) cząstka a przekształca się w atom helu.
Początek „nowożytnej” f. atomowej
Okazało się, że pewna liczba cząstek a rozpraszana jest pod bardzo dużymi katami (prawie 180o). Po przeanalizowaniu wyników Rutherford doszedł do wniosku, że tak silne odchylanie cząstek a możliwe jest jedynie w przypadku, gdy wewnątrz atomu występuje nadzwyczaj silne pole elektryczne wytwarzane przez ładunek związany z dużą masą i skoncentrowany w bardzo małej objętości. Opierając się na tym wniosku Rutherford w 1911 r. zaproponował jądrowy model atomu. Według Rutherforda atom ma postać układu ładunków, w którego środku znajduje się ciężkie dodatnio naładowane jądro o ładunku Ze, o wymiarach nie przekraczających 10-14 m, a wokół jądra w całej objętości zajmowanej przez atom rozmieszczone jest Z elektronów. Prawie cała masa atomu skupiona jest w jądrze.
![]()
Rozwijając teorie rozpraszania cząstek a Rutherford założył dalej, że cząstki a oraz jądro stanowią ładunki punktowe oraz, że prawo Coulomba i prawa mechaniki newtonowskiej są słuszne również dla małych odległości.
gdzie r oznacza odległość cząstki a od jądra atomu folii. Z praw mechaniki wynika, że pod wpływem tego rodzaju siły tor cząstki a ma kształt hiperboli.
Siła odpychająca działa równocześnie na cząstkę a i na jądro atomu, ponieważ jednak jądro złota (Z = 47) ma masę wiele razy większą od masy cząstki a więc można przyjąć, że jądro pozostaje w spoczynku. Jeżeli cząstka a porusza się dokładnie w kierunku jądra, to siła hamująca będzie narastać w miarę zbliżania się cząstki a do jądra aż do do chwili jej zatrzymania, po czym rozpocznie się odpychanie, czyli ruch przyspieszony cząstki a w kierunku przeciwnym, wzdłuż tej samej prostej, po której cząstka zbliżała się do jądra, przy czym cały czas ruch cząstki a odbywa się po linii prostej. w przypadku rozproszenia wstecznego następuje zmiana kierunku toru o 180o. Jest to przypadek bardzo rzadki, gdyż wówczas cząstka a musiałaby się poruszać wzdłuż prostej przechodzącej przez jądro, którego rozmiary są bardzo małe.
Cząstka a, lecąca dokładnie w kierunku jądra, dotarłaby do środka atomu na odległość, którą można wyznaczyć przyrównując energię kinetyczną cząstki do energii
Tak więc wyniki doświadczeń nad rozpraszaniem cząstek a świadczą na korzyść zaproponowanego przez Rutherforda jądrowego modelu atomu. Jednakże ten model okazał się sprzeczny z prawami mechaniki klasycznej i elektrodynamiki. Ze względu na to, że układ nieruchomych ładunków nie może być stabilny, Rutherford zmuszony był zrezygnować ze statycznego modelu atomu i założyć, że elektrony poruszają się wokół jądra po zakrzywionych trajektoriach. Ale w tym przypadku elektron będzie poruszał się z przyspieszeniem, w związku z czym - zgodnie z elektrodynamiką klasyczną - powinien on nieprzerwanie emitować fale elektromagnetyczne. Procesowi emisji promieniowania towarzyszy strata energii, zatem elektron powinien w końcu spaść na jądro.
Model Bohra + postulaty Bohra
W 1913 roku Niels Henrik Bohr opublikował nową teorię budowy atomów. Przyjął on, tak jak wcześniej Rutherford, że elektrony krążą po orbitach kołowych dookoła jądra. Przyjął on jednak trzy nowe tezy:
1. W atomie istnieją takie orbity, po których poruszające się elektrony nie promieniują energii - orbity te nazwał stacjonarnymi.
2. Każda emisja lub też absorpcja energii promieniowania odpowiada przejściu elektronu pomiędzy dwoma orbitami stacjonarnymi. Promieniowanie emitowane w czasie takiego przejścia jest jednorodne i jego częstość określona jest wzorem hv = E1-E2, gdzie h - stała Plancka, E1 i E2 energie układu w obu stanach stacjonarnych.
3. Prawa mechaniki opisują równowagę dynamiczną elektronów w stanach stacjonarnych, ale nie stosują się do przechodzenia elektronu pomiędzy dwoma stanami stacjonarnymi.
Dwa postulaty Bohra:
1.elektron może krążyć po takich orbitach których L=nh; a zatem L=mvr=nh ![]()
2.atom absorbuje lub emituje kwanty hv przechodząc ze stanu (orbity) n→k czyli od energii En-Ek hv=En-Ek
Energia elektronu w atomie wodoru jest sumą energii kinetycznej oraz energii potencjalnej elektrostatycznego oddziaływania elektronu z protonem (jądrem atomowym atomu wodoru). Zgodnie z modelem atomu Bohra, elektron o masie m poruszający się z prędkością V po stacjonarnej orbicie kołowej o promieniu r, posiada moment pędu równy
gdzie h jest stałą Plancka, natomiast n jest liczbą naturalną równą 1, 2, 3… itd (numer orbity). Promienie kolejnych dozwolonych orbit elektronu muszą zatem przyjmować ściśle określone wartości wynikające z powyższej zależności.
Energia całkowita elektronu krążącego po n-tej orbicie w atomie wodoru zależy od promienia orbity a więc nie wszystkie wartości energii elektronu są w atomie dozwolone.
Teoria Bohra atomu wodoru oraz atomu wodoropodobnego
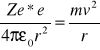
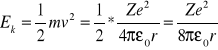
3. Energia w atomie wodoru
![]()
![]()
Jądro ładunku +Ze wytwarza pole potencjalne:
![]()
Zatem e- ma energię potencjalną Ep:
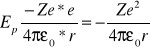
Energia całkowita e-:
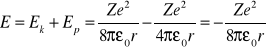
4. Serie widmowe atomu wodoru
Serie widmowe wodoru powstają w wyniku przechodzenia przez elektrony w atomie wodoru z wyższego orbitalu na orbital niższy (tzw. orbital docelowy):
- powstają w wyniku emisji fotonów (np. w rozgrzanym gazie) - widma emisyjne - jasne prążki w widmie
- powstają w wyniku absorpcji fotonów (promieniowanie o widmie ciągłym przechodzące przez gaz) - widma absorpcyjne - ciemne prążki na tle widma ciągłego (fotony z widma ciągłego "pasujące" do przejść są absorbowane, a następnie emitowane - w całości lub w postaci serii przejść - we wszystkich kierunkach, a więc ich intensywność w wiązce wzbudzającej maleje).
hv=En-Ek
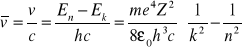
![]()
k- numeruje serie i tak:
k=1 - s. Lymanna(ultrafiolet)
k=2 - s. Balmera (zakres widzialny)
k=3 - s. Paschena (podczerwień)
k=4 - s. Bracketta
k=5 - s. Funda
k=6 - s. Humphreysa
Serie Lymanna(ultrafiolet): ![]()
n = 2, 3 ,4,…
Serie Balmera (zakres widzialny):
![]()
n=3, 4, 5,…
Ogólnie: ![]()
RH - stała Rydberga, RH= 1,09678*107m-1
Pasmowa budowa ciał stałych oraz przewodnictwo samoistne półprzewodników
Półprzewodnikami nazywamy substancje, których przewodnictwo elektryczne jest o kilka rzędów wielkości mniejsze niż u metali. Półprzewodnik samoistny jest to półprzewodnik, którego materiał jest idealnie czysty bez żadnych zanieczyszczeń struktury krystalicznej, których koncentracja elektronów jest równa koncentracji dziur.
półprzewodniki samoistne, półprzewodniki, których przewodnictwo elektr. zależy gł. od liczby przeniesionych wskutek wzbudzenia termicznego elektronów z pasma walencyjnego do pasma przewodnictwa i pozostawionych przez nie w pasmie walencyjnym dziur.
7. Przewodnictwo typu p i n Półprzewodniki samoistne nie posiadają zbyt wielu elektronów swobodnych (co objawia się dużym oporem właściwym, czyli małą konduktywnością), dlatego też stosuje się domieszkowanie. Materiały uzyskane przez domieszkowanie nazywają się półprzewodnikami niesamoistnymi lub półprzewodnikami domieszkowanymi. Domieszkowanie polega na wprowadzeniu do struktury kryształu dodatkowych atomów pierwiastka, który nie wchodzi w skład półprzewodnika samoistnego. Na przykład domieszka krzemu (Si) w arsenku galu (GaAs). Ponieważ w wiązaniach kowalencyjnych bierze udział ustalona liczba elektronów podmiana któregoś z jonów atomem domieszki może spowodować wystąpienie nadmiaru lub niedoboru elektronów. Wprowadzenie domieszki produkującej nadmiar elektronów (w stosunku do ilości niezbędnej do stworzenia wiązań) powoduje powstanie półprzewodnika typu n, zaś domieszka taka nazywana jest domieszką donorową. W takim półprzewodniku powstaje dodatkowy poziom energetyczny (poziom donorowy) położony w obszarze energii wzbronionej bardzo blisko dna pasma przewodnictwa, lub w samym paśmie przewodnictwa. Nadmiar elektronów jest uwalniany do pasma przewodnictwa (prawie pustego w przypadku półprzewodników samoistnych) w postaci elektronów swobodnych zdolnych do przewodzenia prądu. Mówimy wtedy o przewodnictwie elektronowym, lub przewodnictwie typu n (z ang. negative - ujemny).
Wprowadzenie domieszki produkującej niedobór elektronów (w stosunku do ilości niezbędnej do stworzenia wiązań) powoduje powstanie półprzewodnika typu p, zaś domieszka taka nazywana jest domieszką akceptorową. W takim półprzewodniku powstaje dodatkowy poziom energetyczny (poziom akceptorowy) położony w obszarze energii wzbronionej bardzo blisko wierzchołka pasma walencyjnego, lub w samym paśmie walencyjnym. Poziomy takie wiążą elektrony znajdujące się w paśmie walencyjnym (prawie zapełnionym w przypadku półprzewodników samoistnych) powodując powstanie w nim wolnych miejsc. Takie wolne miejsce nazwano dziurą elektronową. Zachowuje się ona jak swobodna cząstka o ładunku dodatnim i jest zdolna do przewodzenia prądu. Mówimy wtedy o przewodnictwie dziurowym, lub przewodnictwie typu p (z ang. positive - dodatni). Dziury, ze względu na swoją masę efektywną, zwykle większą od masy efektywnej elektronów, mają mniejszą ruchliwość a przez to oporność materiałów typu p jest z reguły większa niż materiałów typu n.
8. Powstawanie promieniowania rendgenowskiego - ciągłego i charakterystycznego Promieniowanie rentgenowskie (w wielu krajach nazywane promieniowaniem X lub promieniami X) to rodzaj promieniowania elektromagnetycznego, którego długość fali mieści się w zakresie od 5 pm do 10 nm. Zakres promieniowania rentgenowskiego znajduje się pomiędzy ultrafioletem i promieniowaniem gamma. Znanym skrótem nazwy jest promieniowanie rtg. twarde promieniowanie rentgenowskie - długość od 5 pm do 100 pm
miękkie promieniowanie rentgenowskie - długość od 0,1 nm do 10 nm
Promieniowanie to, odkryte przez Röntgena (nazwane przez niego promieniowaniem X) jest promieniowaniem elektromagnetycznym o długościach od 0.001nm do 10nm. Powstaje ono w wyniku hamowania szybkich elektronów przez substancję. Otrzymać je można za pomocą lamp rentgenowskich, składających się z próżniowego naczynia szklanego lub metalowego, w którym w odpowiedniej odległości od siebie umieszczone są katoda i anoda (zwana też antykatodą) podłączone do wysokiego napięcia, rzędu dziesiątek tysięcy woltów. W lampie panuje próżnia rzędu 10-6mmHg. Z katody emitowane są elektrony, które są przyspieszane przez wytworzone wewnątrz lampy pole elektryczne. Elektrony przy anodzie uzyskują energie rzędu 104-105eV. Elektrony te uderzjąc w anodę (antykatodę) wykonaną z ciężkich metali zostają hamowane, w wyniku czego z anody emitowane jest promieniowanie rentgenowskie.
Stwierdzono istnienie dwóch typów promieniowania rentgenowskiego - ciągłego i charakterystycznego.
Ciągłe promieniowanie rentgenowskie Promieniowanie rentgenowskie o widmie ciągłym zwane także promieniowaniem hamowania (elektronów swobodnych na elektronach związanych) powstaje w wyniku hamowania na antykatodzie elektronów o energiach mniejszych od pewnej energii charakterystycznej dla danego materiału antykatody. Istnieje więc graniczna, minimalna długość fali (charakterystyczna dla danego materiału) jaką uzyskuje promieniowanie ciągłe (wywołane hamowaniem elektronów przyspieszanych określonym napięciem). Jest ona równa:
Na rysunku poniżej podane jest przykładowe widmo ciągłe, wytworzone w lampie, której antykatoda wykonana jest z wolframu. Napięcia przyspieszające elektrony podane są przy krzywych w kV. Dokładnie widać krótkofalową granicę widma ciągłego.
Charakterystyczne (liniowe) promieniowanie rentgenowskie
Mechanizm powstawania linii widma charakterystycznego można wytłumaczyć teorią Bohra W atomach o dużej liczbie atomowej Z powłoki wewnętrzne K (pierwsza powłoka przy jądrze, główna liczba kwantowa n=1), L (n=2), M(n=3) i dalsze są całkowicie wypełnione elektronami. Jeżeli na jednej z nich powstaje puste miejsce (np. wskutek wyhamowania elektronu o bardzo dużej energii), jest ono zajmowane natychmiast przez któryś z elektronów leżących na powłokach dalszych od jądra. Jeśli przejście następuje z wyższej powłoki na powłokę K mówimy o linii K widma rentgenowskiego, przy czym jeśli przejście nastąpiło z powłoki kolejnej, czyli L, linię nazywamy K, jeśli przejście nastąpiło z M na K to powstaje linia K, jeśli z powłoki M na L to linia L itd. Schematycznie powstawanie poszczególnych lini obrazuje poniższy rysunek.
Dla każdego pierwiastka istnieje granica wzbudzenia widma charakterystychnego. Jeśli przykładowo antykatoda wykonana jest z rtęci energia elektronów musi być równa 82 keV, aby mogło zostać wyemitowane promieniowanie charakterystyczne (linia K). Przykładowe widmo charakterystyczne pokazane jest na rysunku poniżej.
9. Prawo Bragga Prawo Wulfa-Braggów - zależność wiążąca stałą sieci krystalicznej d od długości padającego promieniowania i kąta odbicia. Jest jednym z fundamentalnych wzorów stosowanych w rentgenografii strukturalnej i rozmaitych wariantach dyfraktometrii, umożliwiających ustalenie struktury analizowanych substancji na podstawie analizy ich obrazów dyfrakcyjnych. Jej ostateczną postać podali William Henry Bragg i jego syn William Lawrence Bragg w 1913 r.:
Gdzie:
n - liczba nautralna określająca kolejne płaszczyzny sieciowe
λ - długość fali promieniowania rentgenowskiego
d - odległość międzypłaszczyznowa, albo ogólnie średnia odległość powtarzalnych warstw atomów, na których zachodzi rozpraszanie
θ - kąt odbłysku mierzony jako kąt między wiązką promieni pierwotych a płaszczyzna odbijającą.
Wiązki zostają odbite w tym samym kierunku, każda do innej płaszczyzny. Jeżeli różnica tych dwóch dróg będzie równa całkowitej wielokrotności długości fali, to nastąpi wzmocnienie fali odbitej, w wyniku interferencji promieni odbitych.
10. Postulat de Broglie'a oraz doświadczenie potwierdzające falową budowę materii
Podobnie jak promieniowanie EM wykazuje dwoistą naturę tak i cząsteczki.
Dla światła:![]()
zatem ![]()
Podobnie, można przedstawić taką hipotezę dla cząstek: ![]()
lub równoważnie ![]()
lub ![]()
Wzór de Broglie:
Z dyfrakcji
dośw. Ernsta Rutherforda (~1910)
źródło cząstek α
(jądra He)
θ
detektor cząstek α
Folia metal.
rozproszenie:
cząstka naładowana → odpychające oddziaływanie kulombowskie
silne wsteczne rozprosz. → silne oddz.→ silne pola→ ładunek ~ punktowy
brak odrzutu atomów folii → ładunki rozpraszające w ciężkich „obiektach”
~ cała materia folii skupiona w ciężkim jądrze
atomy = ciężkie jądra naładowane dodatnio o b. małych rozmiarach
(~ 10-14 m << rozmiar atomu ~ 10-10 m )
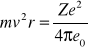
![]()
![]()
![]()
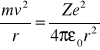
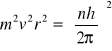
![]()
![]()
Wyszukiwarka
Podobne podstrony:
2LAB, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka -
WYKRES73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
C7, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka - la
Fizzad2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
STOS-EM, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizyka21, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizWyks2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
065S~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizPrad, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
051C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
SUCHY73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
062C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
C 47, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka -
065A~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
LAB9, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
więcej podobnych podstron