Opracowanie: Grzegorz Wilk

WYKŁAD 9

Zbieżność jednostajna

- przestrzeń z miarą

DEFINICJA 9.1 (CIĄG CAUCHY'EGO)

- ciąg Cauchy'ego

co można również zapisać, że

TWIERDZENIE 9.1

W przestrzeni metrycznej każdy ciąg zbieżny jest ciągiem Cauchy'ego

Z:

T:

D: dla
prawdziwe jest:

Wiemy że:
oraz

A więc na podstawie twierdzenia o trzech ciągach stwierdzamy że dla

, co kończy nasz dowód.

Uwaga:

Nie w każdej przestrzeni metrycznej jest prawdziwe twierdzenie odwrotne

(tzn. nie każdy ciąg Cauchy'ego jest ciągiem zbieżnym)

DEFINICJA 9.2 (PRZESTRZEŃ ZUPEŁNA)

Przestrzeń metryczna
jest zupełna
każdy ciąg Cauchy'ego

elementów tej przestrzeni jest zbieżny do granicy należącej do tej przestrzeni

- przestrzeń zupełna

PRZYKŁAD 9.1

1. 
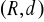
   - przestrzeń metryczna, gdzie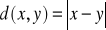
   

przestrzeń ta jest przestrzenią zupełną

2. a)
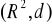
   - przestrzeń metryczna, gdzie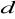
   - odległość euklidesowa

b)
- przestrzeń metryczna, gdzie
- odległość taksówkowa

c)
- przestrzeń metryczna, gdzie
- odległość maksimum

Każda z powyższych przestrzeni metrycznych jest przestrzenią zupełną

3. a)
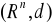
   - przestrzeń metryczna, gdzie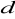
   - odległość euklidesowa

b)
- przestrzeń metryczna, gdzie
- odległość taksówkowa

c)
- przestrzeń metryczna, gdzie
- odległość maksimum

Każda z powyższych przestrzeni metrycznych jest przestrzenią zupełną.

DEFINICJA 9.3 (ZBIÓR ZWARTY (CIĄGOWO ZWARTY))

- przestrzeń metryczna

To znaczy że z każdego ciągu elementów tego zbioru można

wybrać podciąg zbieżny do granicy należącej do tego zbioru.

TWIERDZENIE 9.2

Zbiór
jest zwarty
jest zbiorem domkniętym i ograniczonym

ODWZOROWANIA CIĄGŁE

DEFINICJA 9.4 (OBRAZ I PRZECIWOBRAZ ZBIORU)

- przestrzenie metryczne

- odwzorowanie

Niech

- obraz zbioru
poprzez odwzorowanie

- przeciwobraz zbioru

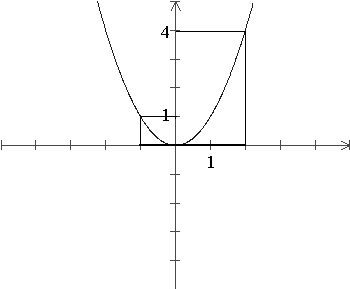
PRZYKŁAD 9.2

;

;

;

DEFINICJA 9.5 (GRANICA FUNKCJI)

- przestrzenie metryczne

- odwzorowanie

1^o. Def. Cauchy'ego (topologiczna)

2^o. Def. Cauchy'ego (w przestrzeni metrycznej)

3^o. Def. Heinego

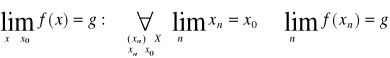
DEFINICJA 9.6 (FUNKCJA CIĄGŁA)

- przestrzenie metryczne

- odwzorowanie

- funkcja ciągła w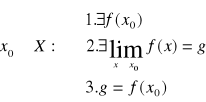

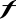
1. 
   - ciągła w zbiorze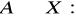
   funkcja f jest ciągła w każdym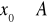
   

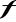
2. 
   - ciągła w zbiorze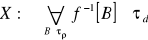
   

słownie:

- ciągła w
przeciwobraz zbioru otwartego (dowolnego) jest zbiorem otwartym

TWIERDZENIE 9.3 (O ZŁOŻENIU ODWZOROWAŃ CIĄGŁYCH)

Z:
- przestrzenie metryczne

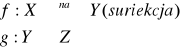
odwzorowanie ciągłe

T:
- ciągłe

D: Niech

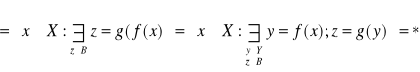
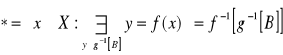
Pokazaliśmy że
, gdzie
, bo
- funkcja ciągła

oraz
bo
- funkcja ciągła

czyli
- funkcja ciągła

DEFINICJA 9.7 (ODWZOROWANIE OGRANICZONE)

- przestrzenie metryczne

- odwzorowanie

- odwzorowanie ograniczone
- ograniczone

WŁASNOŚCI ODWZOROWAŃ CIĄGŁYCH

NA ZBIORACH ZWARTYCH

TWIERDZENIE 9.4

Obraz zbioru zwartego poprzez odwzorowanie ciągłe jest zbiorem zwartym

Z:
- funkcja ciągła;
- zbiór zwarty

T:
- zbiór zwarty

D: Niech

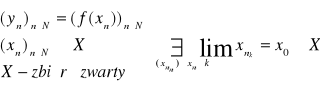
, ponieważ f - funkcja ciągła

oraz

Z ciągu
da się wybrać podciąg
o granicy należącej do tego zbioru.

Czyli zbiór
jest zwarty

WNIOSEK 9.1 (TW. WEIERSTRASSA)

Z:
- przestrzeń metryczna

- odwzorowanie ciągłe,
- zwarty

T:

1^o.

2^o.

słownie:

funkcja ciągła na zbiorze zwartym (o wartościach rzeczywistych) osiąga swoje kresy.

PRZESTRZENIE SPÓJNE

DEFINICJA 9.8 (PRZESTRZEŃ NIESPÓJNA)

- przestrzeń metryczna

- niespójna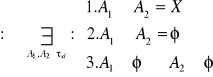

DEFINICJA 9.9 (PRZESTRZEŃ SPÓJNA)

- przestrzeń metryczna

- spójna
nie jest niespójna

WŁASNOŚCI ODWZOROWAŃ CIĄGŁYCH

NA ZBIORACH SPÓJNYCH

TWIERDZENIE 9.5

Z:
- przestrzeń metryczna spójna

- odwzorowanie ciągłe

T:

D: nie wprost

Z:

Niech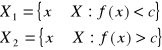

1^o.
, bo f - ciągła i
- zbiór otwarty

, bo f - ciągła i
- zbiór otwarty

2^o.

3^o.

4^o.

Z punktów 1^o do 4^o wynika że
- niespójne,

co jest sprzeczne z założeniem, czyli twierdzenie jest prawdziwe.

WNIOSEK 9.2 (WŁASNOŚĆ DARBOUX)

Z:
- odcinek,
- ciągłe,

T:

WNIOSEK 9.3

Z:
- odcinek,
- ciągłe,

T:

TWIERDZENIE 9.6

Z:
- przestrzeń metryczna,
- spójna

- ciągłe

T:
- spójne

(obraz zbioru spójnego poprzez odwzorowanie ciągłe jest zbiorem spójnym)

D: nie wprost

Niech

Przypuśćmy że
- niespójny

Niech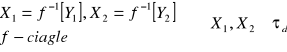

, zatem
- niespójne.

Sprzeczność z założeniem

ZBIEŻNOŚĆ PUNKTOWA I JEDNOSTAJNA

- zbiór,
- przestrzeń metryczna

- ciąg odwzorowań

DEFINICJA 9.10 (ZBIEŻNOŚĆ PUNKTOWA)

(czyt.: powiemy że
jest zbieżny punktowo do
na zbiorze
)

DEFINICJA 9.11 (ZBIEŻNOŚĆ JEDNOSTAJNA)

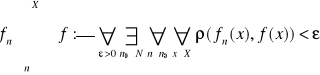
(czyt.:
jest zbieżny jednostajnie do
na
)

PRZYKŁAD 9.3

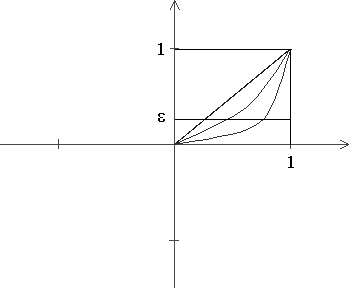
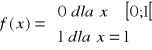
- funkcja graniczna

jest zbieżny punktowo, ale nie jednostajnie.

---