SCHEMAT BERNOULLIEGO - c.d.

Def: Wskaźnik
taki, że
nazywamy najbardziej prawdopodobną liczba sukcesów w serii n doświadczeń.

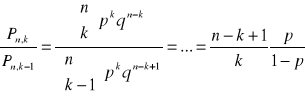
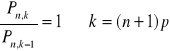
1. gdy
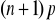
   jest całkowite, to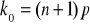
   
   
   

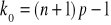
2. gdy
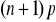
   nie jest całkowite, to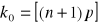
   

- pierwsza seria doświadczeń polegająca na wykonaniu
doświadczeń

- druga seria doświadczeń polegająca na wykonaniu
doświadczeń

- k-ta seria doświadczeń polegająca na wykonaniu
doświadczeń

Tw: Poissona

Jeżeli przeprowadzimy ciąg
serii doświadczeń według schematu Bernoulliego tak, że liczba doświadczeń w poszczególnych seriach dąży do nieskończoności, a prawdopodobieństwo zajścia zdarzenia A
i spełniony jest warunek
, to
.

Dow:

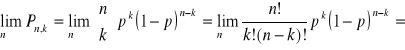
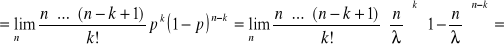
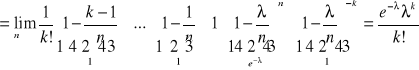
Powyższy wzór daje dobre przybliżenie dla
,
,
.

Np.: Urna zawiera 1 kule białą i 49 czarnych. Losujemy 50 razy po jednej kuli ze zwracaniem. Jakie jest prawdopodobieństwo wylosowania co najmniej 2 razy kuli białej.

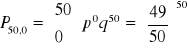
- ciężkie do obliczenia

tworzymy ciąg

Miara Diraca:

- zbiór,
,
,

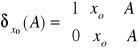
- miara skoncentrowana w punkcie
(Diarca).

Miara Lebesque'a:

Gdy

[długość przedziału na prostej]

Gdy
- dowolny zbiór, to zbiór ten pokrywamy zbiorem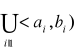
, gdzie
- parami rozłączne.

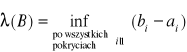
Uwaga:

∅ jeżeli są parami rozłączne

Czyli
nie jest miarą (bo dopuszcza
)

nazywamy miarą zewnętrzną.

Tw: Klasa L

L jest
-ciałem i miara
zacieśniona do L jest miarą.

Def: Zbiory należące do rodziny L nazywamy zbiorami Lebesque'a, a miarę
zacieśnioną do rodziny L - miarą Lebesque'a i oznaczamy
- miara na prostej.

Rozważmy

Def: Przedziałem w
nazywamy zbiór postaci
, gdzie
jest przedziałem na prostej.

Długość przedziału

Objętość

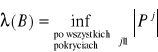
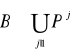
nie jest miarą

L

L
jest miarą

Elementy rodziny L nazywamy zbiorami Lebesque'a w
.
zacieśnione do L nazywamy miarą Lebesque'a w przestrzeni
i oznaczamy
.

1. Każdy zbiór Borelowski jest zbiorem Lebesque'a

2. Miara Lebesque'a jest miarą zupełną

3. Zbiór jednopunktowy ma miarę 0

4. Każdy zbiór przeliczalny ma miarę 0

5. Każdy przedział zdegenerowany (czyli w wyższej przestrzeni, np. odcinek na płaszczyźnie) ma miarę 0

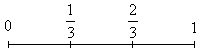
Np.:

Z odcinka
wyrzucamy
i każdy inny środek

C - zbiór Cantora to wszystko to co zostało.

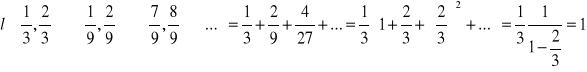
, C jest zbiorem nieprzeliczalnym

ZMIENNA LOSOWA

- przestrzeń z miarą

Oznaczenia:

- przeciwobraz

, to

Def: Funkcję
nazywamy
mierzalną jeżeli

Tw: Jeżeli
, to następujące warunki są równoważne:

Def: Niech
będzie przestrzenią probabilistyczną. Odwzorowanie
nazywamy zmienną losową jeżeli jest ono P-mierzalne.

Wniosek:
jest zmienną losową jeżeli
, tzn. że
jest zdarzeniem

Korzystając z poprzedniego twierdzenia można zauważyć, że jeżeli
jest zmienną losową, to przeciwobraz każdego zbioru B jest zdarzeniem.

Tw: Jeżeli
są zmiennymi losowymi, to

,

,
,

,
,
,
też są zmiennymi losowymi.

Np.: rzucamy kostką do gry, Jeżeli wypadnie mniej niż 6 płacimy 1zł. Jeżeli wypadnie 6 to otrzymujemy 5zł.

, P - prawdopodobieństwo klasyczne

- przestrzeń probabilistyczna

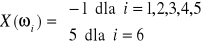
jest zmienną losową

Jeżeli
to każde odwzorowanie
jest zmienną losową.

4

Luke Rachunek prawdopodobieństwa-wykład 5.3.2k+1

---