PRAWO PASCALA: Prawo Pascala odnosi się do cieczy nieściśliwej i ma zastoso­wanie wtedy, gdy ciśnienie wynikające z własnego ciężaru cieczy równa się zeru (np. w stanie nieważkości w sztucznym satelicie) lub jest niewielkie w porównaniu z ciśnie­niem zewnętrznym, tak że można je zaniedbać. Jeśli przyjmiemy dla takiej cieczy nazwę cieczy nieważkiej, to treść prawa Pascala można będzie ująć następująco: w cieczy nie­ściśliwej i nieważkiej ciśnienie zewnętrzne rozchodzi się we wszystkich kierunkach jednakowo. Z prawem Pascala wiąże się działanie prasy hydraulicznej. Jest to urządzenie służące do otrzymywania dużych sił (dużego parcia). ZASADY DLA BRYŁY SZTYWNEJ: I zasada dynamiki dla ruchu obrotowego - jeżeli na ciało sztywne działają siły, których wypadkowe mom. sił względem osi obrotu są równe 0 to ciało pozostaje w spoczynku lub porusza się ze stałą pr. kątową (obraca się ruchem jednostajnie obrotowym). II zasada dynamiki dla ruchu obrotowego - jeżeli na ciało sztywne działa niezrównoważony moment siły, to moment ten nadaje ciału przyspieszenie kątowe, którego wartość jest wprost proporcjonalna do wartości momentu siły i odwrotnie proporcjonalna do momentu bezwładności ciała. Є =M / I		Bryłą sztywną- nazywamy ciało stałe, w którym odległość dwu dowolnie wybranych punktów nie ulega zmianie, mimo działających na to ciało sił.Ruch postępowy br. sztywnej - jest jeżeli wszystkie punkty br. sztywnej mają takie same prędk. liniowe, takie same przyspieszenie, takie same tory.Ruch obrotowy br. sztywnej - to taki ruch, podczas którego wszystkie jej punkty z wyjątkiem tych leżących na osi obrotu, zataczają okręgi o środkach leżących na osi obrotu. Podczas ruchu. obrot. każdy punkt br. sztywnej porusza się z taką samą pr. kątową. Jeżeli prędkość kątowa ruchu obrotowego nie jest stała, wprowadza się pojęcie przyspieszenia kątowego br. sztywnej. Prędkość kątowa (ω) - wartość prędkości kątowej jest równa stosunkowi kąta Δα zakreślonego przez promień przeprowadzony ze środka poruszającego się punktu, do czasu Δt w jakim został on zakreślony => ω = Δα / Δt. Przyśpieszeni kątowe - jest równe stosunkowi przyrostu wektora prędkości kątowej do czasu, w którym ten przyrost nastąpił. Droga kątowa - jest to droga jaką przebywa punkt bryły sztywnej, miarą jej jest kąt zakreślony przez wektor wodzący tego punktu Momentem siły nazywamy wektor będący iloczynem wektorowym siły i wektora r o początku w osi obrotu i końcu w punkcie. Momentem bezwładności ciała obracającego się nazywamy sumę iloczynów mas poszczególnych punktów materialnych tego ciała przez kwadraty odległości tych punktów od osi obrotu. Pęd bryły sztywnej - jest równy iloczynowi momentu bezwładności i prędkości kątowej z jaką ta bryła się porusza.
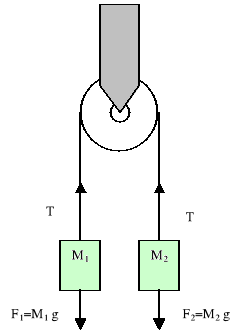
Maszyna Atwooda złożona jest z dwóch mas M1 i M2 połączonych sznurkiem, który przełożony jest przez swobodnie obracający się bloczek. Zwykle sznurek i bloczek traktuje się tak, jakby nie miały masy. Siła, jaką sznurek działa na każdą z mas, nazywa się napięciem T. Napięcie jest takie samo na obu końcach sznurka. Niezrównoważone masy powodują przyspieszony ruch maszyny. 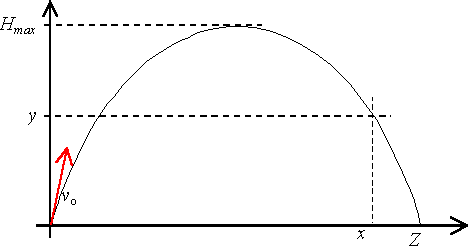Przyśpieszenie może być obliczone tak: Przyspieszenie obciążników w rozważanym eksperymencie może być obliczone teoretycznie ze wzoru: [m/s^2] , - masy obciążników po jednej i drugiej stronie bloczka m - masa bloczka = 20g g = 9.81 m/s^2 - przyspieszenie ziemskie	RZUT UKOŚNY NA PRZYKŁADZIE RZUTÓW OSOBISTYCH DO KOSZA Teoria mówi, że ciało wyrzucone zakreśli tor w kształcie paraboli skierowanej ramionami w dół (oczywiście jeśli opór jest znikomy) i spadnie na ziemię. To właśnie chcieliśmy zaobserwować w doświadczeniu, gdzie badanym obiektem była rzucona piłka do kosza. 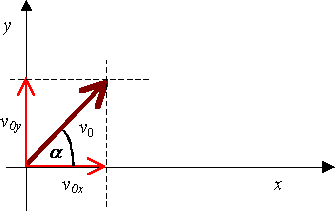W rzucie ukośnym ciału zostaje nadana prędkość początkowa . Z rozkładu prędkości otrzymujemy dwie składowe: prędkość początkowa wzdłuż osi x : , i prędkości początkowej wzdłuż osi y: . Obie prędkości wyrażone są przy pomocy funkcji kąta . Przy znikomym oporze powietrza, gdy występuje brak siły, która mogłaby zmienić prędkość, składowa pozioma pozostaje stała, natomiast składowa pionowa ulega zmianie pod wpływem siły grawitacji. Rzut ukośny jest ruchem o stałym przyspieszeniu g skierowanym w dół. Ponieważ w kierunku poziomym nie działa na ciało żadna siła, więc składowy ruch poziomy jest prostoliniowy i jednostajny. Prędkość w tym ruchu jest stała i równa . W kierunku pionowym działa siła ciężkości wywołując powstanie ruchu jednostajnie zmiennego, o prędkości , zmieniając się z biegiem czasu. A zatem: , . W rzucie ukośnym interesującymi wielkościami są zasięg rzutu Z, maksymalna wysokość l oraz czas lotu. Wiedząc, że możemy obliczyć prędkość początkową : . Maksymalna wysokość wyrzucenia piłki wynosi: . Podstawiając do wzoru na l otrzymujemy: .	Statyka - dział mechaniki zajmujący się równowagą układów sił m.in. równowagą cieczy (hydrostatyka) i gazów Statyka jako dział mechaniki ogólnej wykorzystuje następujące zasady (aksjomaty), których się nie udowadnia, a przyjmuje jako pewniki. Zasada I (zasada równoległoboku). Działanie dwóch sił P1 i P2 można zastąpić działaniem jednej siły R, działającej na ten sam punkt, będącej przekątną równoległoboku ABCD zbudowanego na wektorach sił P1 i P2. Wypadkową R wyznaczamy ze wzoru W przypadku, gdy siły P1 i P2 działają wzdłuż jednej prostej i są zgodnie skierowane, wartość wypadkowej wynosi R=P1+P2 Natomiast, gdy siły są przeciwnie skierowane i P2 =P1 , to R=P2-P1 Zasada druga. Jeżeli do ciała przyłożone są dwie siły, to równoważą się one tylko wtedy, gdy mają tę samą linię działania, te same wartości liczbowe i przeciwne zwroty. Aby siły te równoważyły się, muszą być spełnione zależności Zasada trzecia. Skutek działania dowolnego układu sił przyłożonego do ciała nie zmieni się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił, czyli tzw. układ zerowy. Wynika stąd następujący wniosek: każdą siłę działającą na ciało sztywne można przesunąć dowolnie wzdłuż jej linii działania. Zasada czwarta (zasada zesztywnienia). Jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało doskonale sztywne (nieodkształcalne), identyczne z poprzednim, pod działaniem tego samego układu sił. Wynika stąd wniosek, że warunek konieczny i wystarczający do równowagi ciała sztywnego jest tylko warunkiem koniecznym, ale nie wystarczającym do równowagi ciała odkształcalnego. Zasada piąta (zasada działania i przeciwdziałania). Każdemu działaniu towarzyszy równe co do wartości, o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie. Zasada szósta (zasada oswobodzenia od więzów). Każde ciało nieswobodne można myślowo oswobodzić z więzów, zastępując ich działanie reakcjami, a następnie rozważać jako ciało swobodne znajdujące się pod działaniem sił czynnych i biernych (reakcji więzów).
PRAWO ARCHIMEDESA: Wyobraźmy sobie, że wyodrębniliśmy w cieczy znajdu­jącej się w spoczynku pewną objętość. Na ciecz w tej objętości działa pionowo w dół siła ciężkości P przyłożona w środku ciężkości rozwa­żanej masy cieczy. Jeśli całość cieczy pozostaje w spoczynku, to znaczy, że wspomniana siła ciężkości jest zrównoważona przez oddziaływanie wypadkowe otaczającej cieczy równe też P, lecz skierowane pionowo w górę. Niech ciecz w rozważanej objętości skrzepnie zachowując niezmienioną gęstość. W warunkach równowagi nic nie ulegnie zmianie. Zastąpmy teraz w myśli wyodrębnioną objętość cieczy przez bryłę z dowolnego materiału o tym samym kształcie i rozmiarach. Oddziaływanie ze strony cieczy pozo­stanie niezmienione. Ciało zanurzone będzie podlegało wypadkowemu parciu skierowanemu do góry, zwanemu wyporem. Wypór W jest równy ciężarowi takiej ilości cieczy, która ma objętość równą objętości ciała zanurzonego. Innymi słowy, wypór, jakiemu podlega ciało zanurzone w cieczy, równa się ciężarowi cieczy wypartej przez to ciało		1 ZASADA DYNAMIKI: Jeżeli na ciało nie działają siły zewnętrzne, lub działające siły równoważą się, to ciało pozostaje w spoczynku, lub porusza się ruchem jednostajnym prostoliniowym. Dlatego pierwsza zasada dynamiki jest traktowana jako postulat istnienia inercjalnego układu odniesienia i jest formułowana:Istnieje układ odniesienia, w którym ciało nie podlegające oddziaływaniom zewnętrznym spoczywa lub porusza się po prostej ze stałą prędkością II ZASADA DYNAMIKI: a=F/m Gdy siły działające na ciało nie równoważą się, to ciało porusza się ruchem zmiennym. Kierunek i zwrot tego przyspieszenia są zgodne z kierunkiem siły wypadkowej, a wartość proporcjonalna do wartości siły. Przyspieszenie ruchu ciała jest wprost proporcjonalne do wartości siły, a odwrotnie proporcjonalne do masy ciała.'' [ . Im większa jest siła, tym większe przyspieszenie (zmianę prędkości) może ona wywołać w tym samym czasie.] Im większa jest masa ciała, tym proporcjonalnie większej siły potrzeba, aby wywołać to samo przyspieszenie. II zasada dynamiki określa jak możliwość uzyskania przyspieszenia przez ciało zależy od masy: - ta sama siła cięższemu ciału nadaje mniejsze przyspieszenie. Kinematyka - dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości tego ruchu. Kinematyka abstrahuje od działających sił i bezwładności ciał. Podstawowe pojęcia kinematyki to: przestrzeń, czas, współrzędne, tor ruchu, prędkość, przyspieszenie, prędkość kątowa, przyspieszenie kątowe.

---