Kolokwium wykładowe z kinamatyki

1. Obliczyć wartość iloczynu skalarnego
wektorów o składowych
i 
.

Odp.:
.

2. Obliczyć wartość iloczynu wektorowego
wektorów o składowych
i 
.

Odp.: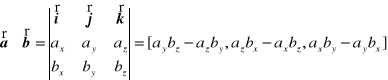
.

3. Obliczyć wartość iloczynu mieszanego
wektorów o składowych
,
i
.

Odp.:

.

4. Uprościć wyrażenie:
.

Odp.: Na podstawie tożsamości
wnioskujemy
.

5. Uprościć wyrażenie:
.

Odp.:
. Na podstawie antyprzemienności iloczynu mieszanego wnioskujemy, że
. Stąd wynika
.

6. Sformułuj i objaśnij twierdzenie o rozkładzie przyspieszenia punktu na przyśpieszenie normalne i styczne.

Odp.:
gdzie
jest przyspieszeniem stycznym,
jest przyśpieszeniem normalnym,
jest jednostkowym wektorem stycznym,
jest krzywizną toru,
jest promieniem krzywizny toru,
jest jednostkowym wektorem normalnym.

7. Dane są równania płaskiego ruchu punktu materialnego:
gdzie
 i 
są stałymi. Wyznaczyć przyspieszenie normalne i styczne w chwili
.

Odp.: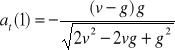
,
.

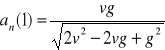
Obliczenia: Na podstawie twierdzenia o rozkładzie przyspieszenia punktu na przyśpieszenie normalne i styczne obliczmy:

a). Wektor prędkości punktu
.

b). Długość wektora prędkości
.

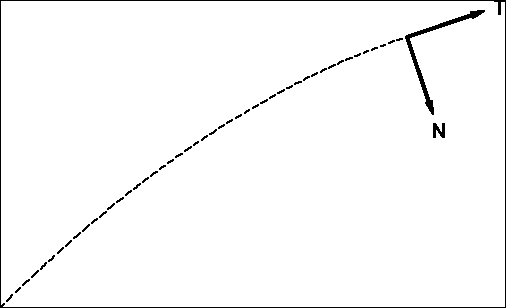
c). Jednostkowy wektor styczny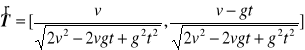
.

d). Jednostkowy wektor normalny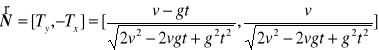
, bo w ruchu płaskim wystarczy obrócić
o -90^o aby otrzymać
.

e). Wektor przyśpieszenia
.

f). Przyspieszenie styczne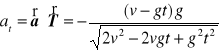
.

g). Przyspieszenie normalne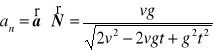
.

h). Wartości chwilowe przyspieszenia stycznego i normalnego:

,
.

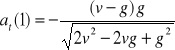
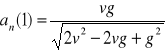
8. Dane są równania płaskiego ruchu punktu materialnego:
gdzie
 i 
są stałymi. Wyznaczyć przyspieszenie normalne i styczne w chwili
.

Odp.: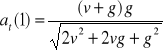
,
.

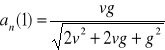
Obliczenia: Na podstawie twierdzenia o rozkładzie przyspieszenia punktu na przyśpieszenie normalne i styczne obliczmy:

a). Wektor prędkości punktu
.

b). Długość wektora prędkości
.

c). Jednostkowy wektor styczny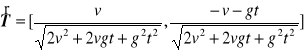
.

d). Jednostkowy wektor normalny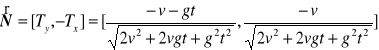
, bo w ruchu płaskim wystarczy obrócić wektor styczny
o -90^o aby otrzymać wektor normalny
.

e). Wektor przyśpieszenia
.

f). Przyspieszenie styczne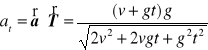
.

g). Przyspieszenie normalne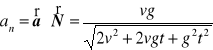
.

h). Wartości chwilowe przyspieszenia stycznego i normalnego:

,
.

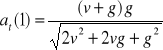
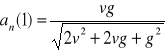
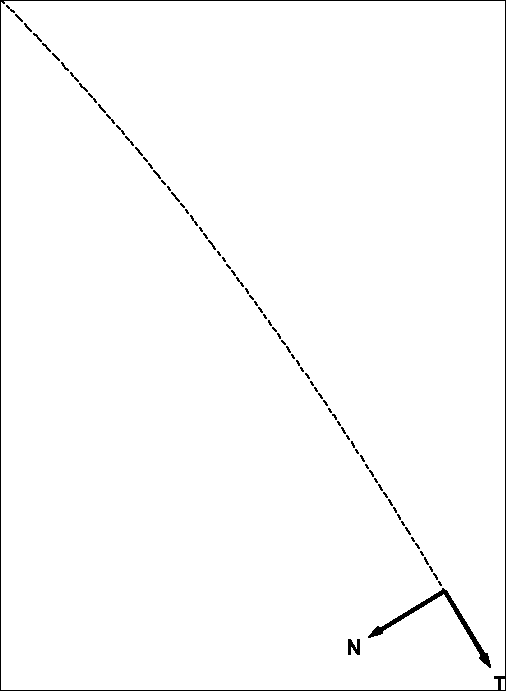
9. Koło o promieniu R toczy się ruchem płaskim po płaszczyźnie bez poślizgu. Wiadomo, że prędkość środka koła
jest stała. Wyznaczyć przyspieszenie punktu odległego o r od środka koła w swym najwyższym/najniższym/dowolnym położeniu.

Odp.:
.

Obliczenia.

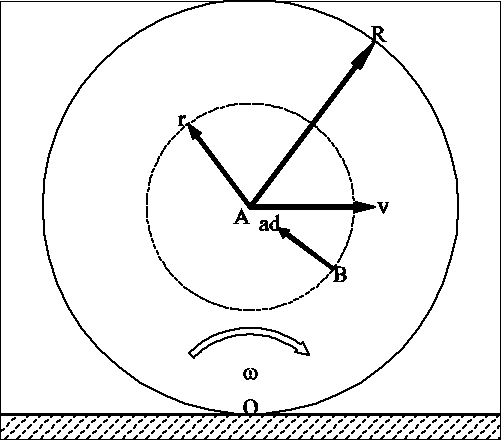
Z twierdzenia o prędkościach punktów bryły
, bo
.

Zatem prędkość kątowa koła wynosi
. Zatem przyśpieszenie kątowe koła wynosi
.

Z twierdzenia o przyśpieszeniach punktów bryły
. Ale przyśpieszenie środka koła wynosi
. Przyśpieszenie obrotowe również znika
. Pozostaje jedynie przyśpieszenie dośrodkowe
.

Uwaga! Jak to zwykle bywa w niniejszym zadaniu przyśpieszenie środka chwilowego obrotu jest niezeroweeeeeeeeeeeeeeeee i wynosi
.

10. Sformułuj i objaśnij twierdzenie o prędkościach i przyśpieszeniach punktów bryły w ruchu kulistym.

Odp.: W ruchu kulistym prędkość i przyśpieszenie punktu bryły o położeniu
względem środka ruchu wynoszą odpowiednio

,

gdzie
jest wektorem prędkości kątowej bryły, a
jest wektorem przyśpieszenia kątowego bryły?

12. Wiadomo, że bryła porusza się ruchem obrotowym ze stałą prędkością kątową
. Obliczyć składowe wektorów prędkości i przyśpieszenia punktu bryły o współrzędnych
względem układu współrzędnych z zerem na osi obrotu.

Odp.:
,
.

Z twierdzenia o prędkościach punktów bryły w ruchu kulistym wynika, że prędkość rozpatrywanego punktu wynosi

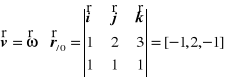
Z twierdzenia o przyśpieszeniach punktów bryły w ruchu kulistym wynika, że przyśpieszenie rozpatrywanego punktu wynosi

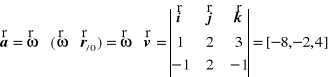
bo
.

13. Wiadomo, że bryła porusza się ruchem obrotowym ze stałą prędkością kątową
. Obliczyć składowe wektorów prędkości i przyśpieszenia punktu bryły o współrzędnych
względem układu współrzędnych z zerem na osi obrotu.

Odp.:
,
.

Z twierdzenia o prędkościach punktów bryły w ruchu kulistym wynika, że prędkość rozpatrywanego punktu wynosi

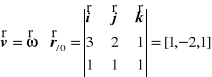
Z twierdzenia o przyśpieszeniach punktów bryły w ruchu kulistym wynika, że przyśpieszenie rozpatrywanego punktu wynosi

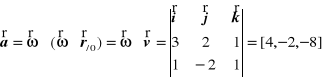
bo
.

14. Wiadomo, że bryła porusza się ruchem kulistym, a punkty A i B mają współrzędne odpowiednio [1,0,0] i [0,1,0] względem układu współrzędnych z zerem w środku ruchu kulistego. Wiadomo również, że składowe prędkości punktów A i B wynoszą odpowiednio [0,3,-2] i [-3,0,1] w tym samym układzie współrzędnych. Wyznaczyć składowe wektora prędkości kątowej bryły.

Odp.:
.

Obliczenia: Z twierdzenia o prędkościach punktów bryły w ruchu kulistym zastosowanego dla punktów A i B wynika

,

.

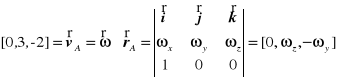
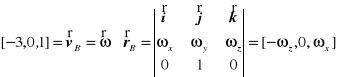
Stąd wnioskujemy, że
,
,
jest rozwiązaniem otrzymanego układu równań.

15. Wiadomo, że bryła porusza się ruchem kulistym, a punkty A i B mają współrzędne odpowiednio [1,0,0] i [0,1,0] względem układu współrzędnych z zerem w środku ruchu kulistego. Wiadomo również, że składowe prędkości punktów A i B wynoszą odpowiednio [0,1,-2] i [-1,0,3] w tym samym układzie współrzędnych. Wyznaczyć składowe wektora prędkości kątowej bryły.

Odp.:
.

Obliczenia: Z twierdzenia o prędkościach punktów bryły w ruchu kulistym zastosowanego dla punktów A i B wynika

,

.

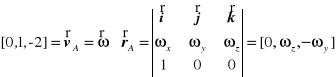
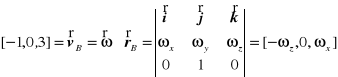
Stąd wnioskujemy, że
,
,
jest rozwiązaniem otrzymanego układu równań.

16. Sformułuj i objaśnij twierdzenie o prędkościach w ruchu złożonym punktu.

Odp.: Jeżeli równania ruchu punktu materialnego przedstawić w postaci

gdzie
są współrzędnymi rozpatrywanego punktu względem zaczepionego w punkcie
ruchomego układu współrzednych o wersorach

to prędkość bezwzględna punktu wynosi
gdzie

jest prędkością względną, a

jest prędkością unoszenia, natomiast
jest wektorem prędkości kątowej ruchomego układu współrzędnych.

17. Sformułuj i objaśnij twierdzenie o przyśpieszeniach w ruchu złożonym punktu.

Odp.: Jeżeli równania ruchu punktu materialnego przedstawić w postaci

gdzie
są współrzędnymi rozpatrywanego punktu względem zaczepionego w punkcie
ruchomego układu współrzednych o wersorach

to przyspieszenie bezwzględne punktu wynosi
gdzie

jest przyśpieszeniem względnym,

jest przyśpieszeniem unoszenia, a

jest przyspieszeniem Coriolisa natomiast
i
są wektorami prędkości i przyspieszenia kątowego ruchomego układu współrzędnych.

Dodatek - Iloczyn wektorowy

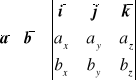
Iloczyn wektorowy jest pseudowektorem, tzn. wynik obliczeń w dwu różnych układach współrzędnych nie zależy od wyboru układu współrzędnych pod warunkiem, że oba układy mają tę samą skrętność a zmienia zwrot na przeciwny w przypadku układów o różnych skrętnościach.

Podstawowe właściwości:

Kierunek iloczynu wektorowego
jest prostopadły do czynników, a zwrot taki, że trójka wektorów
ma taką samą skrętność jak przyjęty układ współrzędnych.

Dodatek - Iloczyn mieszany

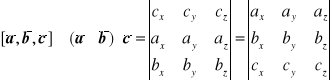
Iloczyn mieszany jest pseudoskalarem, tzn. wynik obliczeń w dwu różnych układach współrzędnych nie zależy od wyboru układu współrzędnych pod warunkiem, że oba układy mają tę samą skrętność a zmienia znak na przeciwny w przypadku układów o różnych skrętnościach.

Podstawowe właściwości:

---