Równania ruchu

Równania ruchu układów dynamicznych rozpoczynamy od zasady Hamiltona. Dla układu zachowawczego wymaga ona, aby całka

(3.2.1.)

miała wartość ekstremalną. Funkcja podcałkowa L reprezentuje nadwyżkę energii kinetycznej nad potencjalną tj.

L = A_k − A_p (3.2.2.)

gdzie:

L - funkcja Lagrange'a

A_k -energia kinetyczna

A_p - energia potencjalna

Po obliczeniu wariacji całki względem kolejnych zmiennych (współrzędnych uogólnionych) otrzymuje się równania Lagrange'a drugiego rodzaju; dla układów zachowawczych, bez strat i bez wymuszenia zewnętrznego:

(3.2.3.)

dla j = 1,..., k

gdzie:

q _j -współrzędne uogólnione

k - liczba stopni swobody

Dla układów niezachowawczych - rzeczywistych, ze stratami i z wymuszeniem zewnętrznym równania Lagrange'a przyjmują postać:

(3.2.4.)

gdzie:

- funkcja strat

- funkcja wymuszenia

3.3. Stabilność oraz stany nieustalone

„Stabilnością układu nazywamy jego skłonność powracania do warunków równowagi statycznej, gdy został z nich wytrącony.”[1]

„Zmiana wartości obciążenia lub siły elektromotorycznej silnika powoduje zakłócenie równowagi ruchu napędu”[1]: zmianę momentu dynamicznego oraz prędkości ruchu. Zakłócenia równowagi ruchu napędu nazywamy stanem nieustalonym, który trwa aż do osiągnięcia nowej stałej prędkości ruchu układu napędowego.

Układ napędowy znajduje się w stanie równowagi gdy M_d = 0 tj. gdy M_s(ω) = M_obc.( ω). Stan równowagi dynamicznej jest punktem pracy układu napędowego: jest to punkt przecięcia się charakterystyki silnika z charakterystyką obciążenia rys. 3.3.1.

Rys. 3.3.1. Punkt pracy układu napędowego [1]

Moment dynamiczny jest różnicą pomiędzy momentem silnika (wymuszeniem zewnętrznym) a momentem oporu (obciążeniem).

(3.3.1.)

3.4. Więzy sprężyste

„Więzy sprężyste charakteryzuje współczynnik sztywności k określany jako wartość siły potrzebnej dla jednostkowego przesunięcia jednego końca więzów względem drugiego. Dla przesunięcia prostoliniowego wartość tego współczynnika można wyznaczyć wg wzoru :

(3.4.1.)

gdzie:

F - siła rozciągająca więzy [N],

∆l - wydłużenie liniowe [m],

E - moduł sprężystości Younga [N / m²],

Q - przekrój poprzeczny [m²],

l - długość więzi [m].

Dla przesunięcia obrotowego współczynnik sztywności jest równy:

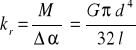
(3.4.2.)

gdzie:

M - moment skręcający więzy [Nm],

∆α - skręcenie więzi [rad],

G - moduł sprężystości poprzecznej [N / m²],

d - średnica więzi [m].”[1]

„Zarówno model mechanizmu jazdy, jak i podnoszenia jest nieswobodnym układem materialnym. Oznacza to, że na niektóre elementy układu nałożone są więzy ograniczające ich swobodę ruchu.

Więzy określone równaniami są więzami dwustronnymi. Jeżeli równanie więzów zawiera tylko współrzędne punktów, to nazywamy je więzami geometrycznymi lub holonomicznymi.

(3.4.3.)

Równania więzów mogą być także zależne od prędkości punktów, wówczas nazywamy je więzami kinematycznymi lub nieholonomicznymi.

(3.4.4.)

Oba rodzaje więzów mogą ponadto zależeć od czasu. Więzy zależne od czasu nazywamy więzami skleronomicznymi lub stacjonarnymi.”[2]

Obliczenia mechanizmu podnoszenia

Obliczenie mechanizmu jazdy

Model matematyczny - dwumasowy

Model mechanizmu podnoszenia służący do badania ruchu sprowadza się do układu dwóch mas zredukowanych połączonych ze sobą elementem sprężystym rys. 6.1.1. Masa m₁ jest to zredukowana na wał wolnoobrotowy reduktora masa, która zastępuje momenty bezwładności elementów obrotowych: wirnika silnika, sprzęgieł, bębna hamulcowego, kół zębatych i bębna z nawiniętą liną. Masa m₂ jest to zredukowana masa zastępująca masę ładunku zawieszonego na linie oraz masę zblocza.

- zredukowana masa zastępująca momenty bezwładności

wirnika silnika, sprzęgieł bębna hamulca, kół zębatych i

bębna z nawiniętą liną ;

- siła zastępcza na obwodzie bębna linowego,

reprezentującą moment silnika ;

- zredukowana masa zastępująca masy ładunku

zawieszonego na haku i zblocza ;

- siła zastępcza reprezentującą ciężar ładunku

zawieszonego na haku i zblocza ;

- zredukowana sztywność lin w układzie

wielokrążkowym zredukowanym do pojedynczej

liny zastępczej ;

- zredukowany współczynnik tłumienia ;

Rys. 6.1.1. Model matematyczny - dwumasowy

6.2. Równania ruchu

ROZRUCH

„W zależności od warunków, w jakich rozpoczyna się rozruch mechanizmu podnoszenia, wartości początkowe przyjmują różne wartości.”[1]

• Przypadek z napiętymi więzami :

Rys. 6.2.1. Model matematyczny - dwumasowy przypadek z napiętymi więzami

Na rysunku 6.2.1. przedstawiono przypadek gdzie obydwie masy startują jednocześnie, a więc ich wartości początkowe są równe zero:

(6.2.1.)

Równania ruchu przyjmują postać:

(6.2.2.)

• Przypadek ze zluzowanymi więzami :

Rys. 6.2.2. Model matematyczny - dwumasowy przypadek ze zluzowanymi więzami

Rysunek 6.2.2. ilustruje nam ładunek spoczywający na podłożu, lina nie jest napięta. Ruch takiego układu rozpoczyna się od fazy napinania więzów, tj. początkowo porusza się tylko masa m₁, co powoduje stopniowe rozciąganie więzów. Faza ta trwa do chwili, w której siła odkształcająca więzy osiągnie wartość równą sile S₂ .

Układ ma tylko jeden stopień swobody, a więc ruch układu opisuje jedno równanie drugiego rzędu.

(6.2.3.)

• Przypadek z nadmiernym luzem w linie :

Rys .6.2.3. Model matematyczny - dwumasowy przypadek z nadmiernym luzem w linie

Na rysunku 6.2.3. ładunek również jak w powyższym przykładzie (rys. 6.2.2.) spoczywa na podłożu, lecz tym razem liny są bardziej luźne. Ruch takiego układu rozpoczyna się od fazy kasowania luzu w więzach - porusza się tylko masa m₁ pociągając za sobą linę bez oporu, a masa m₂ spoczywa swobodnie na podłożu .

Wartości początkowe są równe zero:

(6.2.4.)

W równaniu nie występują zewnętrzne ani wewnętrzne siły oporu.

(6.2.5.)

Ruch jest jednostajnie przyspieszony i trwa do chwili wyczerpania luzu:

(6.2.6.)

Czas kasowania luzów wyraża się wzorem:

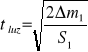
(6.2.7.)

Prędkość masy m₁ w chwili skasowania luzu jest równa:

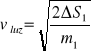
(6.2.8.)

Drugą fazą tego układu jest napinanie więzów, tj. początkowo porusza się tylko masa m₁, co powoduje stopniowe rozciąganie więzów. Faza ta trwa do chwili, w której siła odkształcająca więzy osiągnie wartość równą sile S₂ . Równanie ruchu nie zmienia się, natomiast występują inne warunki początkowe.

(6.2.9.)

Faza ta trwa aż do chwili, w której napięcie więzów zrównoważy siłę obciążającą więź S_2. Wartości
na końcu drugiej fazy są odpowiednio wartościami początkowymi trzeciej fazy ruchu obu mas. Faza ta rozpoczyna się w chwili
, gdy siła naciągu liny zaczyna przekraczać wartość S_2.

HAMOWANIE PRZY OPUSZCZANIU

Podczas hamowania przy opuszczaniu układ sił jest bardzo podobny jak przy rozruchu - przedstawia nam to ilustracja 6.2.4. Zasadnicza różnica polega na zmianie kierunku ruchu mas oraz na tym, że siła S₁ pochodzi od hamulca umieszczonego na wale silnika.

Rys. 6.2.4. Model matematyczny - dwumasowy przypadek hamowania przy opuszczaniu

Warunki początkowe określone są przez prędkość ruchu przy opuszczaniu oraz wydłużenie układu linowego pod wpływem zawieszonego ciężaru

(6.2.10.)

Ruch opisują dwa równania różniczkowe:

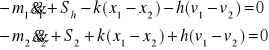
(6.2.11.)

Ruch tego układu składa się z dwóch faz:

− ruch obu mas - trwa do zatrzymania masy m₁ siłą hamulca

− po zatrzymaniu masy m₁
następuje faza, w której masa m₂ wykonuje

swobodne wahania pionowe opisane równaniem:

(6.2.12.)

HAMOWANIE PRZY PODNOSZENIU

Hamowanie podczas podnoszenia można opisać podobnie jak hamowanie podczas opuszczania - rysunek 6.2.5. Istotna różnica polega tylko na tym, że siła S₂ pochodząca od ciężaru współdziała z hamulcem, co przyspiesza proces hamowania.

Rys. 6.2.5. Model matematyczny - dwumasowy przypadek hamowania przy podnoszeniu

Równania ruchu w fazie pierwszej - ruch obu mas:

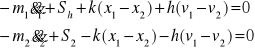
(6.2.13.)

Faza ta trwa aż do chwili

, w której nastąpi zatrzymanie pierwszej masy m₁ ,
. Druga faza po zatrzymaniu masy m₁
to ruch wahadłowy drugiej masy m₂:

(6.2.14)

Obliczenie parametrów występujących w równaniach ruchu

Tab. 6.3.1. Tabela danych obliczeniowych mechanizmu podnoszenia

Nazwa	Oznaczenie	Wartość	Jednostka
Masa podnoszona	mQ	5000	[kg]
Masa zblocza	mQ0	100	[kg]
Wysokość podnoszenia	L	10	[m]
Przełożenie wielokrążnika	iw	2
Sprawność wielokrążnika	ηw	0,99
Średnica liny	d	14	[mm]
Przekrój liny	F	72,5	[mm^2]
Średnica bębna	Db	0,355	[m]
Moc silnika	P	7	[kW]
Obroty silnika	n	940	[obr/min]
Moment bezwładności silnika	Js	0,05	[kgm^2]
Moment bezwładności sprzęgła hamulca	Jsh	0,159	[kgm^2]
Moment bezwładności koła z1	Jz1	0,003	[kgm^2]
Moment bezwładności koła z2	Jz2	0,014	[kgm^2]
Moment bezwładności koła z3	Jz3	0,016	[kgm^2]
Moment bezwładności koła z4	Jz4	0,119	[kgm^2]
Moment bezwładności sprzęgła bębna	Jsb	0,7	[kgm^2]
Moment bezwładności bębna	Jb	6,08	[kgm^2]
Przełożenie 1-st	i1	10,35
Przełożenie 2-st	i2	10,35
Sprawność 1-st	η1	0,98
Sprawność 2-st	η2	0,98
Sprawność bębna	ηb	0,98
Moment hamowania	Mh	200	[Nm]
Luz	δ	0,1	[m]

Obliczenie masy zredukowanej − m₁

(6.3.1)

− obliczenie momentu zredukowane J_zr1 dla masy m₁

(6.3.2)

(6.3.3)

[kgm²]

zatem:
[kg]

• Obliczenie masy zredukowanej − m₂

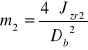
(6.3.4)

− obliczenie momentu zredukowane J_zr2 dla masy m₂

(6.3.5)

gdzie:
(6.3.6)

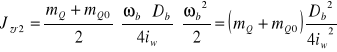
(6.3.7)

[kgm²]

zatem:
[kg]

Obliczenie siły wymuszającej S_1R dla rozruch

(6.3.8)

− obliczenie M^*_silnika

(6.3.9)

(6.3.10)

(6.3.11)

[1/s]

[Nm]

[Nm]

zatem:
[N]

• Obliczenie siły wymuszającej S_2R dla rozruchu

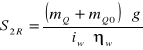
(6.3.12)

[N]

• Obliczenie siły wymuszającej S_1H dla hamowania

(6.3.13)

[N]

• Obliczenie siły wymuszającej S_2H dla hamowania

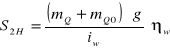
(6.3.14)

[N]

• Obliczenie współczynnika sprężystości liny − k

(6.3.15)

[N/m]

• Obliczenie współczynnika tłumienia − h

(6.3.16)

[N⋅s/m]

• Równania ruch układu

(6.3.17)

− podczas rozruchu

− podczas hamowania

Podsumowanie

Badania symulacyjne dla wariantów hipotetycznych

Badania symulacyjne dla wariantów hipotetycznych

Obliczenia sprawdzające zachowanie się mechanizmu w stanach nieustalonych

Obliczenia sprawdzające zachowanie się mechanizmu w stanach nieustalonych

Budowa modelu dwumasowego

Budowa modelu dwumasowego

Obliczenia i dobory mechanizmu jazdy

Obliczenia i dobory mechanizmu podnoszenia

Wciągarka przejezdna

Zapis wyników

Charakterystyka

momentu obciążenia

Charakterystyka

momentu silnika M_s

Punkt pracy

ω

ω _p

M _obc

M

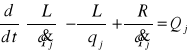
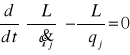
Sprawdzenie poprawności przekładni

Procedury końcowe

Sprawdzenie silnika

Sprawdzenie hamulca

Dobór sprzęgła przybębnowego

Dobór hamulca i sprzęgła hamulcowego

Sprawdzenie poprawności przekładni

Dobór przekładni z katalogu

Obliczenia przekładni zębatej metodą Wissamanna

Wybór sposobu projektu przekładni

Dobór silnika

Wstępne obliczenia do doboru silnika. Wyznaczenie momentów oporu i średniej mocy

Zmiana materiału

Zmiana grubości płaszcza

Dobór materiału na płaszcz bębna i obliczenia wytrzymałościowe

Dobór grubości płaszcza bębna i obliczenia wytrzymałościowe

Obliczanie parametrów geometrycznych bębna

Dobór średnic bębna linowego i krążków linowych

Dobór i sprawdzenie liny

Dobór zblocza

Dane wstępne

Procedury startowe

STOP

Dobór sprzęgieł na wale wolnoobrotowym

Zapis wyników

Sprawdzenie silnika na rozruch i grzanie

Sprawdzenie hamulca

Dobór hamulca, bębna hamulcowego i sprzęgła

Sprawdzenie czy ∆v < ∆v_dop

Dobór silnika

Dobór reduktora

Obliczanie oporów jazdy i mocy średniej

Sprawdzenie luzu koło-szyna

Dobór szyn

Dobór kół jezdnych

Naciski na koła jezdne

Dane wstępne

START

m₁

m₂

m₁

m₂

m₁

m₂

m₁

m₂

m₁

m₂

m₁

m₂

---