dr inż. Krzysztof Chodnikiewicz Rok akademicki: 2010 - 2011

Materiały uzupełniające

D1. Definicje wybranych wielkości fizycznych

Położenie - wektorowa wielkość fizyczna określająca kierunek i odległość danego obiektu od wybranego punktu odniesienia, będącego zazwyczaj początkiem układu współrzędnych. Wektor, który jest utożsamiany z położeniem, nosi nazwę wektora wodzącego. Należy rozróżniać położenie w ruchu prostoliniowym i obrotowym.

Przemieszczenie - różnica pomiędzy dwoma położeniami.

Masa - wielkość fizyczna określająca bezwładność ciał (masa bezwładna) i oddziaływania grawitacyjne między nimi (masa grawitacyjna).

Czas - w fizyce klasycznej samodzielna wielkość, niezależna od innych wielkości, biegnąca w takim samym rytmie w całym Wszechświecie. W mechanice relatywistycznej czas stanowi czwartą współrzędną czasoprzestrzeni, jego upływ zaś zależy od obserwatora i jest różny dla różnych obserwatorów.

Prędkość - wektorowa wielkość fizyczna wyrażająca zmianę wektora położenia w jednostce czasu. Prędkość liniowa dotyczy zmiany położenia w ruchu prostoliniowym. Prędkość kątowa dotyczy zmiany położenia w ruchu obrotowym.

Przyspieszenie - wektorowa wielkość fizyczna, której wartość jest równa wartości pochodnej prędkości względem czasu w danej chwili. Jeśli przyspieszenie jest skierowane przeciwnie do kierunku prędkości ruchu, to jest czasem nazywane opóźnieniem. Tak jak w przypadku prędkości wyróżnia się przyspieszenie liniowe i przyspieszenie kątowe.

Moment bezwładności - miara bezwładności ciała w ruchu obrotowym.

Pęd punktu materialnego - iloczyn masy i prędkości punktu. Pęd jest wielkością wektorową; kierunek i zwrot pędu jest zgodny z kierunkiem i zwrotem prędkości. Pęd układu punktów materialnych jest równy sumie wektorowej pędów, wszystkich punktów układu.

Siła - wielkość wektorowa, miara oddziaływań fizycznych między ciałami. Szczególnym przypadkiem siły jest ciężar.

Moment siły (moment obrotowy) - iloczyn wektorowy siły i promienia wodzącego, którego początek znajduje się w określonym punkcie a koniec w punkcie przyłożenia siły.

Praca - iloczyn skalarny wektora siły działającej na ciało i wektora przesunięcia.

Moc - ilość pracy wykonana w jednostce czasu.

Sprawność - miara jakości przekształcania energii, najczęściej wyrażana w procentach. Jeżeli - przykładowo - sprawność wynosi 80%, to znaczy, ze 80% energii wejściowej zostało przekształcone w energię wyjściową, a 20% zostało w procesie przekształcania stracone.

Wielkość fizyczna	Jednostka	Uwagi:	Najczęściej stosowany symbol:
Odległość, długość, położenie, przemieszczenie liniowe	metr [m]	Jednostki podstawowe układu SI	x
Kąt płaski	radian [rad]			α
Masa	kilogram [kg]			m
Czas	sekunda [s]			t
Prędkość liniowa	m/s		v
Prędkość kątowa	rad/s		ω
Przyspieszenie liniowe	m/s^2		a
Przyspieszenie kątowe	rad/s^2		ε
Moment bezwładności	kgm^2		J
Pęd	kg m/s		p
Siła	(Newton) N=kgm/s^2	Patrz 1)	F
Moment obrotowy	Nm		M
Praca	(dżul) J = Nm		W
Moc	(Wat) W = J/s	Patrz 2)	P

1) W stosowanym szereg lat temu układzie CGS (centymetr, gram, sekunda) jednostką siły była dyna. W Polsce stosowano także jednostkę o nazwie kilogram siły [kG]; w Niemczech - równy mu kilopond [kp]. Jeden kilogram siły jest to siła z jaką Ziemia przyciąga ciało o masie 1 kg. Jednostkę tę można jeszcze spotkać w starych podręcznikach; 1 kG to około 9,80665 N. W Wielkiej Brytanii zamiast oznaczenia kG lub kp używano kgf (kilogram force).

2) 1kW (kilowat), równy 1000W, po wprowadzeniu układu SI, zastąpił konia mechanicznego (KM). Moc silników, szczególnie spalinowych jest często nadal podawana w KM, przy czym 1 KM = 0,735498 kW zaś 1 kW = 1,3596 KM

D2. Wzory określające wybrane wielkości fizyczne

Wielkość fizyczna, symbol	Wzór	Użyte symbole	Uwagi;
Prędkość liniowa, v		s- droga, t - czas;	Wzór słuszny dla ruchu jednostajnego lub dla prędkości średniej
			x - przemieszczenie liniowe	Wzór ogólny
	Prędkość kątowa,		- kąt obrotu	Wzór słuszny dla ruchu jednostajnego lub dla prędkości średniej
				Wzór ogólny
	Przyspieszenie liniowe, a			Wzór słuszny dla ruchu jednostajnie przyspieszonego
				Wzór ogólny
	Przyspieszenie kątowe,			Wzór słuszny dla ruchu jednostajnie przyspieszonego
				Wzór ogólny
Pęd punktu materialnego, p		m- masa
Siła, F
Moment siły, M		r - promień wodzący
			J - moment bezwładności
	Praca, W			Wzór dotyczy ruchu prostoliniowego, słuszny dla F = const
				Wzór ogólny, dotyczy ruchu prostoliniowego
				Wzór dotyczy ruchu obrotowego, słuszny dla M = const
				Wzór ogólny, dotyczy ruchu obrotowego
	Moc, P			Wzór określający moc średnią w czasie t
				Wzór ogólny
				Wzór dotyczy ruchu prostoliniowego
				Wzór dotyczy ruchu obrotowego

Zadania

1. Uzupełnić poniższą tablicę umieszczając w jej kolumnach wielkości analogiczne:

Ruch prostoliniowy	Ruch obrotowy
Przemieszczenie	Kąt obrotu
…..	…..
…..	…..

2. Zakładając, że moc wyjściowa silnika jest stała i wynosi 5kW obliczyć pracę, którą ten silnik wykonuje w ciągu 1 godziny.

3. Załóżmy, że praca obliczona w powyższym zadaniu byłaby zużyta na podniesienie do góry samochodu o masie 1070kg. Na jaką wysokość byłby podniesiony ten samochód?

4. Na tablicy znamionowej starego silnika elektrycznego można odczytać, że moc wynosi 6HP. Ile to kilowatów?

D3. Definicje jednostek podstawowych układu SI

Kilogram - jednostka masy, jednostka podstawowa układu SI, oznaczana kg. Jest to masa międzynarodowego wzorca (walca o wysokości i średnicy podstawy 39 mm wykonanego ze stopu platyny z irydem) przechowywanego w Międzynarodowym Biurze Miar w Sèvres koło Paryża. Wzorzec kilograma został usankcjonowany uchwałą I Generalnej Konferencji Miar w 1889. Jest to obecnie jedyna jednostka podstawowa posiadająca przedrostek (kilo), jak również jedyna, dla której podstawą definicji jest określony przedmiot, a nie odwołanie się do stałych fizycznych. Dawniej za wzorzec był przyjmowany jeden litr wody o temperaturze czterech stopni Celsjusza przy ciśnieniu normalnym. W 1901 r. z kolei 3. Konfrencja CGPM zmieniła definicję litra na objętość jaką zajmuje 1 kg wody destylowaniej w temperaturze 3,98 °C przy ciśnieniu 1 atm = 760 mm Hg (1013,25 hPa). Zależności między litrem i kilogramem usunięto w 1964 r., na 12. konferencji CGPM.

Metr to jednostka podstawowa długości w układach: SI, MKS, MKSA, MTS, oznaczenie m. W myśl definicji zatwierdzonej przez Generalną Konferencję Miar i Wag w 1983 jest to odległość, jaką pokonuje światło w próżni w czasie 1/299 792 458 s.

Sekunda (łac. secunda - następna, najbliższa) - jednostka czasu, jednostka podstawowa większości układów jednostek miar np. SI, MKS, CGS - oznaczana s. Termin sekunda pochodzi od łacińskiego wyrażenia pars minuta secunda (druga mała część). Jest to czas równy 9 192 631 770 okresów promieniowania odpowiadającego przejściu między dwoma poziomami F = 3 i F = 4 struktury nadsubtelnej stanu podstawowego ²S_1/2 atomu cezu ¹³³Cs (powyższa definicja odnosi się do atomu cezu w spoczynku, w temperaturze 0 K). Definicja ta, obowiązująca od 1967 r., została ustalona przez Międzynarodowy Układ Jednostek Miar. Poprzednio sekundę definiowano jako 1/31 556 925,9747 część roku zwrotnikowego 1900 lub 1/86400 część doby.

Stopień - jednostka miary kąta płaskiego równa 1/360 kąta pełnego, czyli 60 minut, czyli 3600 sekund czyli 216000 tercji, nie należąca do układu SI - oznaczenie 1°.

Radian (rad) - jednostka miary kąta płaskiego, jednostka uzupełniająca układu SI.

Jest to kąt płaski równy kątowi między dwoma promieniami koła, wycinającymi z okręgu tego koła łuk o długości równej promieniowi. 1° = (π/180) rad = 60′

Amper - prąd o natężeniu 1 A jest to stały prąd elektryczny, który płynąc w dwóch równoległych, prostoliniowych, nieskończenie długich przewodach o znikomo małym przekroju kołowym, umieszczonych w próżni w odległości 1 m od siebie, spowodowałby wzajemne oddziaływanie przewodów na siebie z siłą równą 2*10 ^-7 N na każdy metr długości przewodu.

D4. Sprawność układu napędowego

Sprawność nie jest pojęciem jednoznacznym. Pozostając przy znaczeniu ściśle technicznym, należy rozróżnić sprawność chwilową i sprawność średnią, wyznaczoną w określonym czasie. Można je zdefiniować następująco:

- sprawność chwilowa

η = Moc uzyskana (wyjściowa) / Moc włożona (wejściowa)

- sprawność średnia (w określonym okresie czasu)

η = Praca uzyskana (wyjściowa) / Praca włożona (wejściowa).

Zastosowanie w definicjach dwóch różnych wielkości fizycznych wynika stąd, że moc może być określona dla danej chwili, natomiast praca zawsze dotyczy określonego czasu. Niekiedy mogą powstać nieporozumienia dotyczące wejścia i wyjścia danego układu lub urządzenia. Dlatego, w każdym przypadku, powinny być one precyzyjnie określone.

Elementy układu, dla którego określa się sprawność, mogą być połączone szeregowo lub równolegle .

W przypadku połączenia szeregowego (rys.2.6) sprawność całego układu wynosi

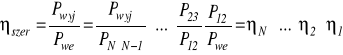
W przypadku połączenia równoległego wzór jest bardziej skomplikowany i najprościej będzie rozpatrzyć konkretny przykład. Niech to będzie układ składający się z dwóch pomp, P1 i P2, napędzanych jednym silnikiem S jak na rys.2.7.

.

Moc wyjściowa pompy jest równa iloczynowi
gdzie Q jest wydajnością zaś p ciśnieniem wyjściowym pompy. Moc wyjściowa układu pomp połączonych równolegle wynosi

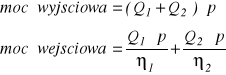
Sprawność układu pomp połączonych równolegle jest więc równa

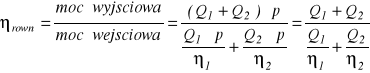
Przykład

Pompy P1i P2 mają jednakowe wydajność 50 litrów na minutę każda. Sprawności się różnią: η₁ = 60%, η₂ = 85%. Obliczyć sprawność układu tych pomp połączonych szeregowo (a) i połączonych równolegle (b).

(a)
0,51 (51%)

(b)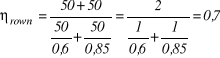
(70%)

Zadanie: Wytłumaczyć, nie odwołując się do wzorów, dlaczego w powyższym zadaniu wystąpiła tak znaczna różnica pomiędzy wynikami (a) i (b).

Zadanie

Dwie pompy hydrauliczne tworzą zespół. Są one połączone równolegle. Wydajność pierwszej wynosi 100 l/min, jej sprawność - 55%. Wydajność drugiej 200 l/min, sprawność - 68%. Obliczyć wydajność i sprawność zespołu.

D5. Sprawność typowych urządzeń technicznych według : D.R. Wulfinghoff, „Energy Efficiency Manual”, 1999.

Energy Conversion Device	Energy Conversion	Typical Efficiency, %
Electric heater	Electricity/Thermal	100
Hair drier	Electricity/Thermal	100
Electric generator	Mechanical/Electricity	95
Electric motor (large)	Electricity/Mechanical	90
Battery	Chemical/Electricity	90
Steam boiler (power plant)	Chemical/Thermal	85
Home gas furnace	Chemical/Thermal	85
Home oil furnace	Chemical/Thermal	65
Chemical/Thermal	Electricity/Mechanical	65
Home coal furnace	Chemical/Thermal	55
Steam turbine	Thermal/Mechanical	45
Gas turbine (aircraft)	Chemical/Mechanical	35
Gas turbine (industrial)	Chemical/Mechanical	30
Automobile engine	Chemical/Mechanical	25
Fluorescent lamp	Electricity/Light	20
Silicon solar cell	Solar/Electricity	15
Steam locomotive	Chemical/Mechanical	10
Incandescent lamp	Electricity/Light	5

D6. Frezarka FWA-32M

Frezarki FWA-32A były produkowane w latach siedemdziesiątych XX wieku. W wielu przedsiębiorstwach są one nadal z pożytkiem używane. Warto porównać schemat kinematyczny tej tokarki (patrz niżej) z rys.1.11, punkt 1.5 wykładu, na którym przedstawiono szkic frezarki CNC.

D7. Model

W naukach technicznych, ale nie tylko, bardzo często używane jest „model”. Na poniższym rysunku pokazano klasyfikacje modeli. W naukach technicznych rozpatruje się najczęściej modele symboliczne, w szczególności matematyczne.

W książce p.t. “Computer simulation and modeling” jej autor F.Neelamkavil podaje następującą definicję modelu: „A model is a simplified representation of a system (or process, or theory) intended enhance our ability to understand, predict, and possibly control the behavior of the system”.

Należy z naciskiem podkreślić, ze „najlepszy” model nie istnieje. Model powinien być tak prosty jak to tylko możliwe, a jednocześnie wystarczający do opisania zjawisk, które dzięki modelowi mają być zrozumiane lub przewidziane. Jest to wskazówka bardzo ogólna, ale trudno podać lepszą. Ogólność powyższej wskazówki jest powodem, że w budowie modeli, szczególnie matematycznych, ogromna rolę gra doświadczenie. Należy podkreślić, że do budowy prostych modeli „zmusza” bardzo często niepełna znajomość wartości liczbowych wielkości występujących w modelu. Istotnie! Stosunkowo łatwo można zmierzyć masę, trudniej moment bezwładności i sprężystość, a jeszcze trudniej cechy tłumiące układu. Podobnie, trudno jest określić niektóre wartości liczbowe charakteryzujące silniki elektryczne.

D8. Zarys numerycznych metod rozwiązywania równań różniczkowych zwyczajnych

Jeżeli na podstawie Drugiej Zasady Dynamiki Newtona (1643-1727) obliczy się przyspieszenie, to wyznaczenie prędkości, a następnie przemieszczenia wymaga rozwiązania równań różniczkowych. Trudności ze ścisłym rozwiązaniem równań spowodowały poszukiwanie rozwiązań przybliżonych. Większość takich rozwiązań opracowano wiele lat temu, jednak ich zastosowanie było ograniczone, gdyż metody rozwiązywania równań różniczkowych wymagają wielkiej liczby operacji arytmetycznych, co przed wprowadzeniem do nauki i techniki komputerów (dawniej mówiono o maszynach matematycznych) było niezwykle utrudnione, jeżeli w ogóle możliwe. Nadto, rozwiązywanie „na piechotę” było ze względu na możliwość popełnienia błędu ogromnie ryzykowne. W metodach przybliżonych, powszechnie nazywanych numerycznymi, wykonuje się operacje na liczbach, a nie na symbolach. Jest to niedogodność, gdyż rozpatrywane jest konkretne równanie, a nie typ równania.

Nazwa najprostszej metody wywodzi się od Eulera (1707-1783). Współcześnie powszechnie jest stosowane są metody Rungego-Kutty. C.D.T.Runge żył w latach 1856-1927; M.W.Kutta - w latach 1867 - 1944. Lata te podano w celu udokumentowania twierdzenia, że metody numeryczne powstały znacznie wcześniej niż zbudowano pierwszy komputer („Collosus”, 1943). Obecnie komputery i kalkulatory programowalne „same” rozwiązują skomplikowane układy równań różniczkowych, a użytkownik na ogół nie ma pojęcia jak to się dzieje. Warto jednak takie pojęcie mieć i celowi temu służą poniższe informacje.

Rozwiązywanie równań różniczkowych zwyczajnych przy znanych warunkach początkowych matematycy nazywają „rozwiązywaniem zagadnień początkowych równań różniczkowych zwyczajnych”.

Zauważmy, że wystarczy podać metodę rozwiązania dla równania pierwszego rzędu, gdyż równanie drugiego rzędu

,

może być, dzięki podstawieniu, sprowadzone do poniższego układu równań pierwszego rzędu

W powyższym zapisie operator
zastąpiono symbolem „bis”, zaś operator
- symbolem „prim”. Rozpatrzmy więc równanie pierwszego rzędu, które ma postać

.

Zakładamy, że równanie to obowiązuje w przedziale
i że znany jest warunek początkowy:
. Metodę Eulera określa wzór, który wynika z definicji pochodnej

Dolny indeks n oznacza poprzedni krok całkowania, dolny indeks n+1 - krok następny, zaś h jest długością kroku całkowania (rys.4.6).

Łatwo zauważyć, że dokładność (inaczej: błąd) metody zależy od wartości kroku. Dla metody Eulera znane jest oszacowanie błędu; istnieje także dowód zbieżności metody (patrz np. Andrzej Krupowicz: Metody numeryczne zagadnień początkowych równań różniczkowych zwyczajnych. PWN, Warszawa, 1980). Zbieżność oznacza, że zmniejszanie kroku powoduje zmniejszanie się błędu.

Wykonajmy jeden krok metody Eulera rozwiązując równanie

uwzględniając, że dla t = 0 jest y = 0. Wyznaczmy człony wyrażenia określającego rozwiązanie przyjmując, że n = 0. Otrzymuje się

Załóżmy, że h = 0,1. Otrzymujemy

Porównajmy uzyskane rozwiązanie z rozwiązaniem ścisłym, które dla rozwiązywanego równania i danego warunku początkowego ma postać

Podstawiając t = h = 0,1 otrzymuje się

czyli już w pierwszym kroku popełnia się błąd rzędu 10%. Można byłoby ten błąd zmniejszyć zmniejszając krok.

Metody (proszę zauważyć liczbę mnogą) Rungego-Kutty zapisujemy w postaci

n = 0, 1, 2, …

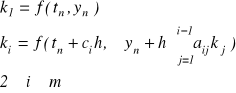
gdzie
zaś w_i, c_i, a_ij są znanymi liczbami. Dla jednej z metod, która jest stosowana w praktyce i jest po prostu nazywana metodą Rungego-Kutty, obowiązują wzory

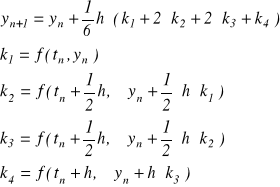
Powróćmy do równania
i wykonajmy jeden krok obliczeniowy stosując powyższe wzory i zakładając h = 0,1

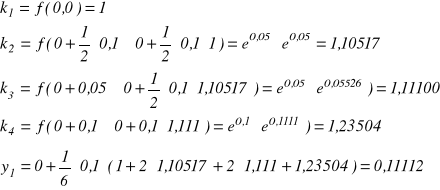
Porównując otrzymany wynik z wynikiem uzyskanym na podstawie rozwiązania ścisłego stwierdzamy, że z dokładnością do piątego miejsca po przecinku (taka dokładność była ustawiona na kalkulatorze), wyniki są identyczne.

Zadanie

Powyżej wykonano pierwszy krok obliczeniowy metoda Eulera i Rungego-Kutty dla równania
przy założeniu kroku h = 0,1. Powtórzyć te obliczenia, przyjmując dla metody Eulera h = 0,05, a dla metody Rungego-Kutty h = 0,2. Wyciągnąć wnioski.

D9. Kilka informacji dotyczących historii silników elektrycznych

W 1832 r. Anglik William Sturgeon wynalazł komutator, co umożliwiło budowę silnika prądu stałego, którego wał obracał się (rys.). Silnik Sturgeon'a zawierał w sobie wszystkie podstawowe części współczesnych silników. Najmniejsze silniki prądu stałego mają moc ułamkową, największe - ponad 1MW. Silnik prądu przemiennego został wynaleziony przez przypadek w 1868r. Belg, Zenobie Gramme połączył ze sobą dwie wynalezione przez siebie prądnice; druga zaczęła pracować

jako silnik. W 1888 r. Nikola Tesla zbudował pierwszy silnik prądu przemiennego, który został zastosowany praktycznie. Pierwsze silniki prądu przemiennego wyprodukowała istniejąca do dnia dzisiejszego amerykańska firma Westinghouse. Współczesne silniki prądu przemiennego maja moc od kilkuset W do kilkuset kW. Ocenia się, że około 80% eksploatowanych na świecie silników to silniki prądu przemiennego.

1

P2

p

Rys.D4.1.6

P_wyj

P₂₃

2

N

..…

1

P_we

P₁₂

P_{N-1 N}

η₁

Fizyczny

Model

h

Wygląd zewnętrzny

Rys.D4.2

Pompa P1: wydajność Q₁, sprawność η₁

Pompa P2: wydajność Q₂, sprawność η₂

S

P1

η₂

η_N

Symboliczny

Mentalny

Składa się z elementów, które można dotknąć.

Zależności matematyczne, symboliczne lub logiczne, mapy, wykresy, rysunki, itp.

Istnieje tylko w umyśle; niemożliwy do przekazania.

Matematyczny

Równania algebraiczne

Równania różniczkowe

Niematematyczny

Statyczny

Dynamiczny

Rys.5.1. Model silnika Williama Sturgeon'a.

Rys.4.6

y_n+1

t_n+1

t_n

t

y

y_n

---