1. WSTĘP TEORETYCZNY

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie współczynnika polaryzowalności elektronowej wody.

2. Schemat układu pomiarowego

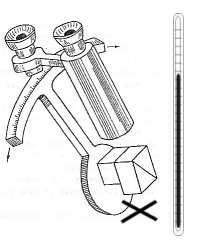
Układ pomiarowy stanowi refraktometr Abbego, którego układ termostatujący połączony jest z układem pompującym ultratermostatu. Ponieważ w ćwiczeniu mierzymy zależności współczynnika załamania wody od temperatury, więc metalowe oprawki pryzmatów muszą być termostatowane. Realizuje się to przepuszczając przez metalowe oprawki pryzmatów wodę termostatującą z termostatu. Przy włączeniu do sieci zostaje uruchomiony silnik poruszający wewnątrz termostatu mieszadełko, służące do wyrównania temperatury kąpieli, jednocześnie zostaje stworzona możliwość włączenia systemu podgrzewającego jego kąpiel. Do tego celu służy kontaktowy termometr rtęciowy, zamocowany w otworze pokrywy. Podgrzewana woda za pomocą pompki tłoczona jest poprzez węże do oprawki pryzmatów pomiarowych refraktometru.

3. Co będziemy mierzyć?

Będziemy mierzyć wartość współczynnika załamania wody w zależności od temperatury.

4. Co będziemy obliczali?

Będziemy obliczali współczynnik polaryzowalności elektronowej wody oraz błędy pomiarów (względny błąd graniczny i błąd bezwzględny wyznaczenia współczynnika polaryzowalności).

Przy wyznaczaniu współczynnika polaryzowalności wody będziemy korzystać ze wzoru Lorentza-Lorentza:

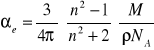
gdzie (dla wody):
n - współczynnik załamania światła,

- masa molowa wody,

- gęstość wody w danej temperaturze,

- stała Avogadra

2. OPRACOWANIE WYNIKÓW POMIARU

1. tabela pomiarów

LP	Temperatura (ºC)	Współczynnik załamania			wartości pomocnicze
				1 pomiar (ogrzewanie)			2 pomiar (ochładzanie)	wartość średnia
1	20	1,3334	1,3330	1,33320	26,664	400
2	25	1,3329	1,3322	1,33255	33,314	625
3	30	1,3322	1,3312	1,33170	39,951	900
4	35	1,3316	1,3308	1,33120	46,592	1225
5	40	1,3309	1,3301	1,33050	53,220	1600
6	45	1,3301	1,3297	1,32990	59,846	2025
7	50	1,3294	1,3293	1,32935	66,468	2500
	245			9,31840	326,054	9275

2. wykres zależności współczynnika załamania od temperatury

Zależność jest liniowa, a więc wykresem będzie prosta:

Do jej wyznaczenia zastosuję metodę regresji liniowej:

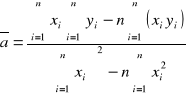
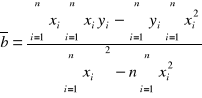
Za n przyjmujemy 7 (ilość pomiarów przy ogrzewaniu), za x_i podstawiamy kolejne wartości temperatur, a y_i odpowiednie wartości średnie współczynnika załamania.

Mamy, że:

wstawiając do powyższych wzorów otrzymujemy:

oraz

tangens konta nachylenia wykresu wynosi
.

3. współczynnik polaryzowalności wody

Współczynnik polaryzowalności wyznaczamy korzystając ze wzoru Lorentza-Lorenza:

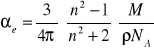
gdzie n - współczynnik załamania światła,
- masa molowa wody,
- gęstość wody w danej temperaturze,
- stała Avogadra

Dla temperatury 35ႰC wartość współczynnika wynosi:

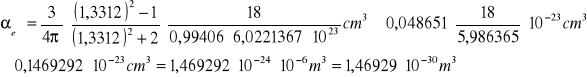
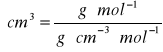
Dla pozostałych temperatur wartość współczynnika polaryzowalności wody wynosi:

Temperatura (ႰC)	Gęstość wody ( )	Współczynnik polaryzowalności wody ( )
20	0,99823	1,47117
25	0,99707	1,47027
30	0,99567	1,46892
35	0,99406	1,46929
40	0,99224	1,46916
45	0,99025	1,46968
50	0,98807	1,47069
Wartość średnia		1,46989

4. błędy pomiarów

Graniczny błąd względny polaryzowalności
wyznaczamy korzystając z prawa przenoszenia błędów:

gdzie: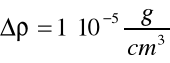
- graniczny błąd wyznaczenia gęstości wody,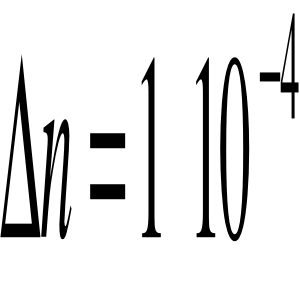
- graniczny błąd odczytu współczynnika załamania światła

Dla temperatury 35ႰC graniczny błąd względny (podany w procentach) wynosi:

Graniczny błąd bezwzględny polaryzowalności

Dla temperatury 35ႰC:

Temperatura (ႰC)	Graniczny błąd względny (%)	Błąd bezwzględny ( )
20	0,028	0,000042
25	0,028	0,000042
30	0,028	0,000042
35	0,028	0,000042
40	0,029	0,000042
45	0,029	0,000042
50	0,029	0,000042

3. WNIOSKI

Wyniki doświadczenia jednoznacznie wskazują na to, że współczynnik polaryzowalności wody nie jest zależny od temperatury. Zmienia się on bardzo nieznacznie. Obliczona przeze mnie wartość średnia tego współczynnika wynosi:

LITERATURA

S. Bartnicki, W. Borys T. Kostrzyński: Fizyka ogólna, ćwiczenia laboratoryjne, cz. I, WAT Warszawa 1994

1

---