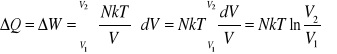1. Teoria przewodnictwa w metalach. Przewodnictwo - to przenoszenie ładunku elektrycznego przez ciało pod działaniem zewnętrznego pola elektrycznego. Elektrony w sieci krystalicznej odrywają się one od swoich atomów i zaczynają swobodnie poruszać się w całej objętości metalu, tworząc tzw. gaz elektronowy.
Przewodnictwo w metalach jest ściśle związane teorią kwantowa metali. W myśl tej teorii w krysztale metalicznym zewnętrzne elektrony atomów nie są związane z poszczególnymi atomami na skutek falowej natury elektronów. Z kwantowej teorii bezpośrednio wynika także, iż te elektrony przewodnictwa mogą przebyć wiele średnic atomowych nim zderza się z innym atomem. Jako L oznaczymy średnią drogę swobodną, jaka przebywa elektron miedzy kolejnymi zderzeniami. Średnim czasem miedzy zderzeniami będzie Δt=L/u gdzie u jest średnią prędkością elektronów przewodnictwa. Gdy do kawałka metalu zostanie przyłożone napięcie to każdy elektron przewodnictwa będzie działał siłą eE, a po czasie Δt każdy z tych elektronów osiągnie prędkość unoszenia vd=Δu wyprowadzona z II prawa Newtona

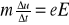
gdy zastąpimy Δt średnim czasem L/u otrzymujemy wzór:

Prędkość unoszenia dla wszystkich elektronów ma ten sam kierunek(-E) i powstaje wypadkowy prąd. Po każdym zderzeniu elektron traci swa prędkość.

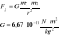
2. Rozkłady natężenia pola elektrycznego od wybranych rozkładów ładunku.

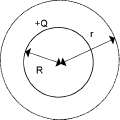
Jednorodnie naładowana sfera

Rozpatrzmy jednorodnie naładowana powierzchnie kulista.

W dowolnym punkcie sfery E \ \ S (prostopadłe do powierzchni) wiec

Zgodnie z prawem Gaussa:

E(4πr²) = Q/Eo

Czyli:

dla r> R (tak jakby cały ładunek skupiony był w środku sfery). Dla r<R, E=0.

Jednorodnie naładowana kula

Przewodniki - równoważne sferze, bo ładunek na powierzchni. Izolator - równoważny szeregowi współśrodkowych sfer.

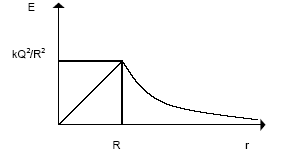
gdzie Q_wewn. = Q{rⁱIR³') (stosunek objętości kuli o promieniu r do objętości kuli o pro­mieniu i?, rysunek).

Wykres E w funkcji odległości od środka jednorodnie naładowanej kuli jest pokazany obok.

Liniowe rozkłady ładunków

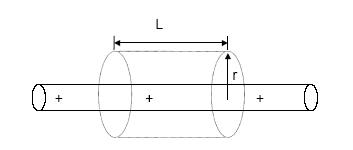
Liczymy pole E w odległości r od jednorodnie naładowanego pręta (drutu) o długo­ści r.

Wprowadzamy liniowa gestosc ładunku A (ładunek na jednostkę długości). Jako powierzchnie Gaussa wybieramy walec (możemy wybierać dowolnie). Z prawa Gaussa

E jest równoległe do wektora S i ma taka sama wartość w każdym punkcie powierzchni wiec

Teraz pole wewnątrz. Wybieramy powierzchnie Gaussa o promieniu r <R.

Ładunek wewnątrz powierzchni Gaussa Q_wew„. = ro*pi*r*L, gdzie ro - gestosc objętościowa ładunku. Z prawa Gaussa otrzymujemy

Płaskie rozkłady ładunków

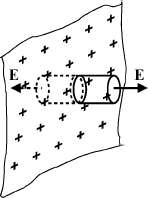
Obliczamy pole od nieskończonej jednorodnie naładowanej płaszczyzny.

Ładunek otoczony przez powierzchnie Gaussa jest równy Q_wewn = oS, gdzie o jest ge-stoscia powierzchniowa, a S powierzchnia podstawy walca. Z prawa Gaussa

gdzie czynnik 2 odpowiada dwom podstawom walca. Ostatecznie otrzymujemy

Wiele zastosowań dotyczy układu dwóch, płaskich równoległych płyt (kondensator płaski).

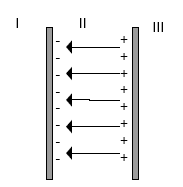
*Pole wytwarzane przez płytę "po lewej stronie" (rysunek poniżej) jest równe E_minus=σ/2ε₀ i skierowane ku płycie.

Pole wytwarzane przez płytę po prawej E_plus=σ/ε₀ i skierowane jest od płyty.

5. Opis cyklu Carnota. Sprawność silnika na bazie cyklu Carnota.(silnik idealny)

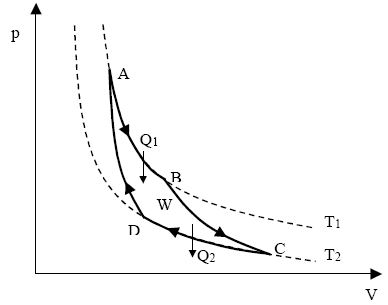
-Rozprężanie izotermiczne A->B

-Rozprężanie adiabatyczne B->C

-Sprężanie izotermiczne

C->D

-Sprężanie adiabatyczne

D->A

Sprawność silnika wynosi: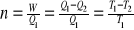

3. Prawa Gaussa dla elektrostatyki.

Powierzchnia zamknięta Z i umieszczone w nim 2 ładunki Q1 i Q2. Całkowita liczba linii sił przecinających tę powierzchnię jest równa:

Φcałk=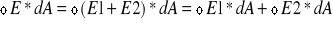

korzystając ze wzoru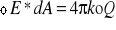

ko-współczynnik proporcjonalności (Coulomba) otrzymujemy

Φcałk=(4πkoQ1)+(4πkoQ2)=4πko*(Q1+Q2)

Dla układu n ładunków wewnątrz zamkniętej powierzchni:

Qwewn- wypadkowy ładunek zawarty wewnątrz zamkniętej powierzchni.

Jeżeli Q jest ujemne to linie wchodzą do ciała.

Każda linia wchodząca do obszaru zawartego wewnątrz powierzchni musi z niego wychodzić. Więc wypadkowa liczba linii wychodzących z tego obszaru jest równa zeru. ( Linia wchodząca jest linią ujemna, a linia wychodząca dodatnią). Ciała przeważnie można podzielić na dwa rodzaje: przewodzące (przewodniki) i nie przewodzące ( izolatory).

Na podstawie prawa Gaussa można stwierdzić, że wypadkowy ładunek wewnątrz przewodnika jest równy zero.

4. Porównanie siły grawitacyjnej i elektrostatycznej.

Wartość siły grawitacyjnej wyraża się wzorem:

Fg - siła grawitacyjna,

G - stała grawitacji,

m_1 oraz m_2 - masy ciał,

r - odległość między środkami ciał.

Wartość siły oddziaływania dwóch ładunków punktowych (elektrostatycznej - kulombowskiej) wyraża się wzorem

F_e - siła kulombowska,

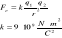
k - stała(współczynnik proporcjonalnosci),

q_1 oraz q_2 - ładunki,

r - odległość między ładunkami.

Ne-liczba elektronów Np.-liczba protonów Ne>Np

q1=q2=(Ne-Np)*e; m1=m2=Ne*me+Np*mp; Ne~=Np -prawie rowne

Me jest znikoma w porównaniu do mp, wiec:

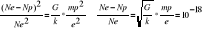
Siła grawitacji jest 10^(-18) razy słabsza.

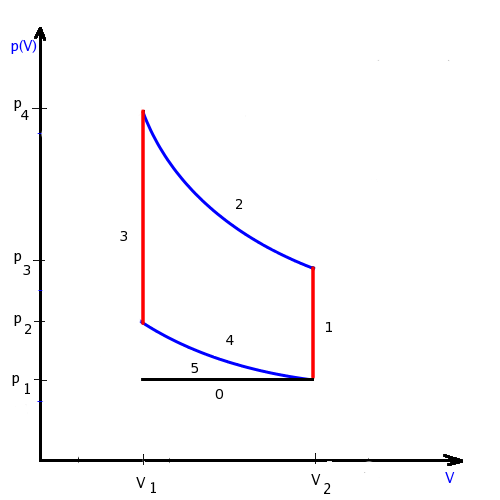
6. Cykl i sprawność silnika Otta.

odwracalny proces kołowy składający się z następujących czterech procesów składowych:

1-sprężanie adiabatyczne

2-ogrzewanie izochoryczne (wskutek spalania mieszanki, silnik spalinowy)

3-ekspansja adiabatyczna

4-chłodzenie izochoryczne

Sprawność: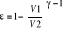

gdzie:

R - stała gazowa

cv - ciepło właściwe

Na zasadzie cyklu Otta działają tłokowe silniki spalinowe z zapłonem iskrowym.

7. Cykl i sprawność silnika Diesla.

Cykl składa się z następujących procesów:

1-izobaryczne rozprężanie - w silniku Diesla w tym etapie spalana jest mieszanka tak, by następowało podgrzanie przy stałym ciśnieniu (rozprężanie z objętości V1 do objętości V2)

2-adiabatyczne rozprężanie - z V2 do V3

3-izochoryczne sprężanie - stała objętość V3

4-adiabatyczne sprężanie - do objętości V1

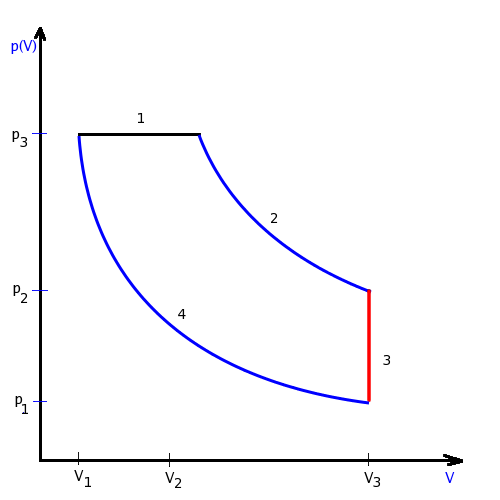
Sprawność cyklu:

gdzie:

cv - ciepło właściwe przy stałej objętości

cp - ciepło właściwe przy stałym ciśnieniu

γ=cp/cv

Ten silnik wymaga dobrego chłodzenia i mocnej konstrukcji.

8. Praca wykonywana przez gaz w trakcie rozprężania adiabatycznego.

Przemiana adiabatyczna- proces termodynamiczny, podczas którego wyizolowany układ nie nawiązuje wymiany ciepła, lecz całość energii dostarczana lub odbierana z niego jako praca

i jest równy zaznaczonemu polu pod krzywą na wykresie. Ponieważ:

, więc
, po podstawianiu tego do całki otrzymujemy:

9. Praca wykonywana przez gaz w trakcie rozprężania izotermicznego.

Przemiana izotermiczna - w termodynamice przemiana, zachodząc przy określonej, stałej temperaturze

.

Z 1 termodynamiki,
. Ponieważ dla rozprężania izotermicznego
, więc mamy

Dla gazu doskonałego za wyrażenie podcałkowe podstawiamy:

11. Prawo Archimedesa.

Siła wyporu działająca na ciało zanurzone w płynie jest równa ciężarowi płynu wypartego przez to ciało

Wzór na siłę wyporu

F_wyporu = ρ_płynu * g * V_zanurzona

gdzie:

ρ_płynu - gęstość płynu [w układzie SI w kg/m^3]

V_zanurzona - objętość tej części ciała, która jest zanurzona w płynie [w układzie SI w m^3]

g - przyspieszenie ziemskie [w układzie SI w m/s^2]

10. Ciepło właściwe w przemianie izobarycznej i izochorycznej.

Molowe ciepło właściwe gazu jest to ilość ciepła potrzebna do podniesienia temperatury 1 mola gazu o 1 stopień.

Ciepło właściwe w stałej objętości:

Symbol C_V

dU=dQ-PdV podstawiając tu dV=0 otrzymamy dQ=dU a stąd mamy i skoro
dla mola jednoatomowego gazu doskonałego, zatem
czyli

Średnia energia wewnętrzna na cząsteczkę wynosi:

, a dla 1 mola wynosi:

Ciepło właściwe przy stałym ciśnieniu:

Symbol C_P

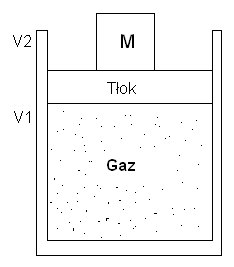
Jeśli mol gazu utrzymujemy pod stałym ciśnieniem i pozwalamy ciepłu dopływać do gazu, to wzrośnie jego objętość i pewna ilość ciepła PΔV zamieni się w pracę mechaniczną. Zgodnie z

dQ=dU+PdV. (1)

Skoro U zależy od T więc:

dU=CVdT (2)

dQ=CVdT+PdV (3)

Dla gazu doskonałego:

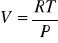
i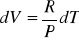

Po podstawieniu tego równania (3) mamy:

co z definicji jest równe C_p czyli ciepłu właściwemu przy stałym ciśnieniu. Tak więc dla gazu doskonałego mamy: C_P-C_V=R

12. Równanie gazu doskonałego.

Gaz doskonały - zwany gazem idealnym jest to gaz spełniający następujące warunki:1- brak oddziaływań międzycząsteczkowych w gazie, z wyjątkiem odpychania w momencie zderzeń cząsteczek;2-objętość cząsteczek jest znikoma w stosunku do objętości gazu;3-zderzenia cząsteczek są doskonale sprężyste

Równanie stanu - równanie Clapeyrona

Pełna postać równania stanu gazu doskonałego jest następująca:

pV=nRT

i nazywane jest ono równaniem Clapeyrona. Przy czym: P oznacza ciśnienie gazu, V - objętość, T - temperaturę, n - liczbę moli gazu a R jest tzw. stałą gazową równą R = 8, 314 J/mol·K.

pV =NkT

gdzie k=R/NA jest stałą Boltzmanna

Boyle'a: p*V=nm(V^2)/3 => 1 stop. Swob.= 0.5kT

13. Trzy zasady termodynamiki.

Zerowa zasada termodynamiki

Izolowane ciała będące w kontakcie ze sobą osiągają równowage termiczną,tzn Ek1=Ek2

Zasada Ekwipartycji Energii

Średnia energia kinetyczna przypadająca na każdy stopień swobody będzie jednakowa dla wszystkich cząstek i rowna 0.5*kT T-temp. k-stala boltzmana =1,38*10^(-23)J*K^-1

Uwew=1.5nkT n-ilosc czasteczek Energia wew. Gazu jest to suma energii kine. wszystkich cząsteczek tego gazu. Dla cz. 2-atom: Uwew=2.5nkT dla cz 3-atom lub wiecej Uwew=3nkT

Pierwsza zasada termodynamiki

∆Q=∆Uwew+∆W

Zmiana energii wewnętrznej układu jest równa sumie pracy wykonanej przez ten układ bądź nad układem i ciepła dostarczonego lub oddanego przez układ.

∆Uwew=∆Q-∆W ∆W=P*∆V P-cisnienie V-objętość

Na podstawie tej pracy => http://fsphost.com/blazej/pk/fiza_egz2.doc

Przerobione i poprawione przez: Adi, Bart i Rafcio

---