Refrakcja i wyznaczanie momentu dipolowego

Heterojądrowa cząsteczka dwuatomowa, na przykład HF lub HCl, jest polarna. Oznacza to, że ma ona różny od zera elektryczny moment dipolowy. Wypadkowy rozkład ładunków w takiej cząsteczce jest równoważny układowi, w którym dwa jednakowe, co do bezwzględnej wartości, lecz przeciwnego znaku ładunki punktowe +q i -q są rozsunięte na odległość r. Taki układ ładunków przedstawiany jest jako wektor, nazywany elektrycznym momentem dipolowym, μ, który skierowany jest od ładunku ujemnego do dodatniego. Wartość momentu dipolowego μ jest równa μ = qr.

Cząsteczka polarna jest to cząsteczka posiadająca trwały moment dipolowy. Pochodzi on od znajdujących się na atomach ładunków cząstkowych, których pojawienie się jest wynikiem różnic elektroujemności atomów lub innych cech wiązania.

Dla cząsteczek wieloatomowych moment dipolowy jest sumą wektorową momentów dipolowych zlokalizowanych w różnych częściach cząsteczki, której wartość liczbowa i kierunek wynikają z przestrzennego rozkładu jąder i elektronów.

(1)

gdzie r_i jest wektorem wodzącym ładunku q_i.

Momenty dipolowe mają wymiar ładunek·długość. Wartości momentów dipolowych są nadal powszechnie podawane w debajach, D, które nie są jednostkami SI. 1 D jest wartością momentu dipolowego pochodzącego od dwóch ładunków o wartości jednej jednostki elektrostycznej ładunku, rozsuniętych na odległość 1 Å (angstrem) (1 Å = 10^-10 m = 10^-8 cm).

Moment dipolowy pary ładunków +e i −e odległych o 100 pm (100 x 10­^-12 m czyli 1 Å) jest równy 1,6⋅10⁻²⁹ C⋅m, co odpowiada 4,8 D. Typowa wartość momentu dipolowego małych cząsteczek to około 1 D (1,08 D dla HCl i 0,42 D dla HI). Bardzo przybliżona zależność miedzy momentem dipolowym, μ w debayach, i różnicą elektroujemności dwóch atomów, Δχ, jest następująca:

(2)

Atom o wyższej elektroujemności jest zwykle ujemnym biegunem dipola, lecz zdarzają się wyjątki, zwłaszcza wtedy, kiedy zajęte są orbitale antywiążące.

Cząsteczka wieloatomowa jest niepolarna, jeśli spełnia pewne kryteria dotyczące symetrii, które są bardziej istotne niż to, czy atomy w cząsteczce są takie same czy też różne. Na przykład homojądrowa trójatomowa cząsteczka ozonu, O₃ (która jest kątowa podobnie jak cząsteczka wody) jest polarna, ponieważ gęstość elektronowa centralnego atomu O jest różna od gęstości na skrajnych atomach. Heterojądrowa trójatomowa cząsteczka, CO₂ (która jest liniowa) jest niepolarna ze względu na symetrię, mimo że atomy C i O mają różne elektroujemności. Momenty dipolowe odpowiadające każdemu z wiązań, CO są skierowane przeciwnie i redukują się wzajemnie.

Przybliżony moment dipolowy cząsteczki można obliczyć metodą dodawania wektorowego, rozpatrując udziały wnoszone przez poszczególne ugrupowania wchodzące w skład cząsteczki. Możemy łatwo stwierdzić, że 1,4-dichlorobenzen ma zerowy moment dipolowy, ponieważ dwa równe, lecz przeciwne, co do znaku momenty dipolowe, związane z obecnością atomów Cl po przeciwnych stronach pierścienia znoszą się. Cząsteczka 1,2-dichlorobenzenu ma trwały moment dipolowy, który w przybliżeniu jest wypadkową dwóch momentów dipolowych, monochlorobenzenu, ustawionych względem siebie pod kątem 60^o.

Wypadkowy moment dipolowy dwóch momentów dipolowych tworzących ze sobą kąt θ można wyliczyć z zależności

(3)

Gdy dwa momenty dipolowe są równe, równanie to upraszcza się do

(4)

Można wykazać, że średni moment dipolowy cząsteczek próbki cieczy jest równy zeru w nieobecności orientującego pola elektrycznego. W obecności pola o natężeniu E w temperaturze T średni moment dipolowy jest niezerowy i wynosi

(5)

gdzie z jest kierunkiem przyłożonego pola. Ta niezerowa wartość wynika z faktu, iż pewne orientacje momentów dipolowych są energetycznie bardziej uprzywilejowane niż inne.

Umieszczenie dielektryka w polu elektrycznym, na przykład między okładkami kondensatora, powoduje rozseparowanie ładunków dodatnich i ujemnych. Mówimy, że pole elektryczne wywołuje polaryzację w dielektryku.

Polaryzacja, P, próbki jest gęstością elektrycznego momentu dipolowego cząsteczki; wyraża się ją jako iloczyn średniego elektrycznego momentu dipolowego cząsteczki,
, i liczby cząstek w jednostce objętości (gęstości liczbowej), N

N

Polaryzacja może zachodzić na dwu różnych drogach: możemy mieć do czynienia z efektem indukcyjnym oraz orientacyjnym. Efekt indukcyjny występuje w każdym dielektryku, bez względu na to, czy zawiera on cząsteczki polarne czy też niepolarne i polega na odkształceniu rozkładu elektronowego i zmianie położeń jąder. Powstający w cząsteczkach niepolarnych indukowany moment dipolowy jest jedynie chwilowy i znika, gdy tylko usunięte zostanie pole zaburzające. Przyłożone pole elektryczne może również przejściowo zmodyfikować trwały moment dipolowy cząsteczek polarnych. Jeśli dielektryk składa się z cząsteczek polarnych, które są trwałymi dipolami, to pole elektryczne powoduje ich orientację zgodnie z kierunkiem pola. Ruchy termiczne cząsteczek przeciwdziałają temu porządkującemu działaniu pola i dlatego polaryzacja orientacyjna maleje ze wzrostem temperatury.

Indukowany moment dipolowy, μ^*, jest proporcjonalny do natężenia działającego pola, E:

E (6)

Stała proporcjonalności α nosi nazwę polaryzowalności cząsteczki. Polaryzowalność ma wymiar, C²·m²·J⁻¹. Im większa jest polaryzowalność cząsteczki, tym większy moment dipolowy może w niej indukować przyłożone pole. Dzieląc wartość polaryzowalności przez iloczyn
(
= 8,854…·10^-12 C²⋅J⁻¹⋅m⁻¹ jest przenikalnością elektryczną próżni) otrzymujemy objętość polaryzowalnościową
:

[7]

Łatwo sprawdzić, że
ma wymiar objętości. Objętości polaryzowalnościowe są porównywalne z rzeczywistymi objętościami cząsteczek (rzędu 10⁻³⁰ m³ = 1 ų). Polaryzowalność rośnie ze wzrostem rozmiarów cząsteczki i jest tym większa, im łatwiej cząsteczka może być wzbudzona.

Zarówno polaryzowalność, jak i polaryzacja wykazują cha­ra­kter wielkości addytywnych.

Polaryzację ogólną, P_og, można przedstawić jako sumę trzech udziałów:

- polaryzacji orientacji, P_or, wynikającej z obecności cząsteczek o trwałych momentach dipolowych, które w polu elektrycznym orientują się zgodnie z kierunkiem linii sił pola,

- polaryzacji atomowej (odkształcenia), P_at, związanej z wywołaną przez pole zmianą położeń jąder atomowych; cząsteczka jest zginana lub rozciągana przez przyłożone pole i odpowiednio do tego zmienia się moment dipolowy,

- polaryzacji elektronowej, P_el, pochodzącej od zmiany rozkładu gęstości elektronowej pod wpływem pola.

(8)

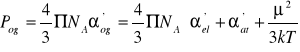
(9)

Polaryzacja zależy od częstości przyłożonego pola. Gdy przyłożone pole zmienia kierunek wolno, cząsteczki o trwałych momentach dipolowych są w stanie nadążać za zmianami kierunku pola elektrycznego. Jednakże, jeśli częstość pola jest zbyt wysoka, cząsteczka nie może zmienić orientacji wystarczająco szybko, aby nadążyć za zmianą kierunku przyłożonego pola i moment dipolowy nie wnosi udziału do polaryzacji próbki. Ponieważ cząsteczka potrzebuje około 1 ps (pikosekunda) (1 ps = 10^-12 s), aby obrócić się w cieczy o kąt około 1 radiana, efekt polaryzacji orientacji zanika wtedy, gdy pomiary wykonuje się przy częstościach większych od 10⁻¹¹ Hz (w zakresie mikrofalowym). Polaryzacja atomowa zanika przy częstościach wyższych od częstości oscylacji atomów w cząsteczce (zakres podczerwieni), ponieważ czas potrzebny na zgięcie cząsteczki jest w przybliżeniu równy odwrotności częstości oscylacji cząsteczki. Przy wyższych częstościach, w zakresie widzialnym, tylko elektrony są wystarczająco ruchliwe, aby odpowiedzieć na szybko zmieniający się kierunek przyłożonego pola. Obserwowany wtedy efekt polaryzacji związany jest tylko z polaryzacja elektronową. Zanika ona, gdy częstość pola przekracza częstość odpowiadającą wzbudzeniom elektronowym.

Kwantowomechaniczne wyrażenie opisujące polaryzowalność cząsteczki w obecności pola elektrycznego oscylującego z częstością ω jest następujące

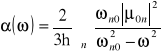
(10)

W równaniu tym
jest wielkością dipolowego momentu przejścia



, gdzie μ jest operatorem elektrycznego momentu dipolowego. Całka ta jest miarą stopnia, w jakim przesunięty jest ładunek elektryczny, gdy elektron przechodzi ze stanu podstawowego o energii E₀, opisanego funkcją falową
, do stanu wzbudzonego o energii E_n, opisanego funkcją falową ψ_n. Sumowanie prowadzi się po stanach wzbudzonych o energiach E_n. Równanie (9) jest słuszne pod warunkiem, że ω nie jest bliskie
, przy czym,
. Z równania (9) wynika, że polaryzowalność sukcesywnie maleje ze wzrostem częstości padającego promieniowania, a gdy ω staje się znacznie większe od częstości wzbudzenia cząsteczki, polaryzowalność zmierza do

Względna przenikalność elektryczna

Energia potencjalna oddziaływania dwóch ładunków
i
znajdujących się w odległości r w próżni jest równa

(11)

Gdy te same dwa ładunki znajdują się w ośrodku (na przykład w powietrzu lub cieczy), ich energia potencjalna ulega obniżeniu, a energia oddziaływania wyraża się wzorem

(12)

gdzie ε jest przenikalnością elektryczną ośrodka. Względna przenikalność elektryczna ośrodka, ε_r, zwana też stałą dielektryczną (wielkość bezwymiarowa) definiowana jest jako

(13)

Względną przenikalność elektryczną substancji mierzy się, porównując pojemność kondensatora w obecności próbki i kondensatora pustego, (C i
) i stosując wzór
.

Względna przenikalność elektryczna jest duża, jeśli cząsteczki są polarne lub w dużym stopniu polaryzowalne.

Równanie Debye'a, słuszne w przypadku, gdy cząsteczki mają swobodę rotacji, podaje ilościową zależność między względną przenikalnością dielektryczną a polaryzacją molową ośrodka:

(14)

gdzie ρ jest gęstością masową próbki, M jest masą molową cząsteczki, a P_m. jest polaryzacją molową, którą definiuje się jako

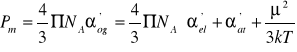
(15)

gdzie

- człon μ²/3kT pochodzi od termicznego uśrednienia elektrycznego momentu dipolowego w obecności przyłożonego pola (równanie (5)). Polaryzacja molowa ma wymiar objętości przez mol.

Z równań (14) i (15) wynika następująca zależność

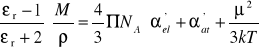
(16)

Z równania (16) wynika, że można wyznaczyć doświadczalnie polaryzowalność i trwały moment dipolowy. W tym celu należy zmierzyć ε_r i gęstość substancji w różnych temperaturach, obliczyć P_m mnożąc uzyskane wartości przez M/ρ, i sporządzić wykres P_m jako funkcji 1/T. Nachylenie wykresu jest równe
, a punkt przecięcia z osią dla 1/T = 0 odpowiada
. Równanie (16) stanowi podstawę metody wyznaczania momentu dipolowgo cząsteczek w fazie gazowej.

Gdy nie obserwuje się wkładu do polaryzacji pochodzącego od trwałych elektrycznych momentów dipolowych, związek między przenikalnością elektryczną substancji tworzącej fazę objętościową a polaryzowalnością jej niepolarnych cząsteczek przedstawia równanie Causiusa-Mosottiego:

(17)

Współczynnik załamania światła

Współczynnik załamania, n_r, definiuje się jako stosunek prędkości światła w próżni, c, do prędkości światła, c', w ośrodku

(18)

Współczynnik załamania światła zmienia się z długością fali; przykładowe wartości współczynników załamania światła o różnych długościach fali dla kilku substancji podano poniżej.

Współczynniki załamania przy różnych długościach fali względem powietrza w 20^oC

434 nm 589 nm 656 nm

C₆H₆(c) 1,524 1,501 1,497

CS₂(c) 1,675 1,628 1,618

H₂O 1,340 1,333 1,331

KI(s) 1,704 1,666 1,658

Z równań Maxwella wynika, że współczynnik załamania dla częstości z zakresu widzialnego lub nadfioletowego jest związany ze względną przenikalnością elektryczną dla tej częstości następującą zależnością:

(19)

Zależność ta jest spełniona, jeśli:

- substancja nie zawiera trwałych dipoli

- współczynnik załamania nie jest mierzony dla promieniowania o długościach fali absorbowanych przez substancję.

Jeśli współczynnik załamania mierzy się w zakresie światła widzialnego, to tylko elektrony są w stanie dostosować się do szybkozmiennego pola elektrycznego i lewa strona równania (20) odpowiada polaryzacji elektronowej.

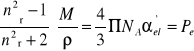
(20)

Wielkość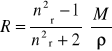
(21)

nazwano refrakcją molową - ma ona sens fizyczny polaryzacji elektronowej.

Refrakcja właściwa definiowana jest jako

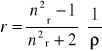
(22)

Standardową długością fali, przy której wyznacza się współ­czynnik załamania światła, jest żółta linia sodu D (λ = 589,3nm). Wartość refrakcji wyznaczona w ten sposób jest ozna­czana jako R_D. Wskutek dyspersji współczynnika zała­mania świat*a (czyli zależności n od długości fali) wartość
jest nieco większa od przenikalnoś­ci elektrycznej substancji, która wykazywałaby tylko polaryzo­walność elektronową.

Z doświadczenia wiadomo, że dla niektórych cząsteczek w stosowanych warunkach pomiarowych może wystąpić również polaryzacja atomowa, P_a; jej udział organicznych ogólnej polaryzacji cząsteczek organicznych jest nieznaczny (zwykle około 10% polaryzacji elektronowej).

Przenikalność elektryczną mierzy się przy niskich częstościach, przy których możliwy jest ruch jąder atomowych, dlatego też na ich podstawie wyznacza się sumę P_a + P_e.

Na podstawie powyższych rozważań możemy zauważyć, że podstawiając równania (20) i (21) do równania (16) otrzymamy

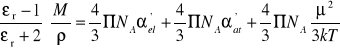
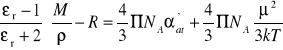
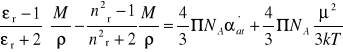
(23)

Z ostatniego równania wynika, że pomiar współczynnika załamania, przenikalności elektrycznej i gęstości w różnych temperaturach pozwala na wyznaczenie momentu dipolowego i polaryzacji atomowej. Zależność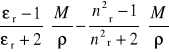
od odwrotności temperatury jest linią prostą o nachyleniu
, a punkt przecięcia z osią dla 1/T = 0 odpowiada
.

Stosowanie tej metody dla układów występujących w fazie ciekłej jest ograniczone ze względów eksperymentalnych. Aby zapewnić swobodę reorientacji czą­ste­czek polarnych w zewnętrznym polu elektrycznym, pomiary n i ε dla substancji ciekłych przeprowa­dza się dla roztworów bardzo rozcieńczonych, używając jako roz­puszczalnika substancji niepolarnej, na przykład CCl₄ lub benzenu. W celu wyeliminowania oddziaływań między cząsteczkami polarnymi konieczna jest ekstrapolacja wartości polaryzacji orientacyjnej do rozcieńczeń nieskończenie wielkich.

Refrakcja wykazuje charakterystyczną właściwość, addytywnoś­ci. Wielkość refrakcji molowej może być rozłożona na (a): udziały atomowe, z uwzględnieniem poprawek strukturalnych, noszących nazwę inkrementów, lub (b): refrakcje odpowiednich wiązań pomiędzy różnymi atomami. Przykładowe wartoś­ci zebrano w tabelach 1a i 1b.

Tabela 1a.

Refrakcje atomowe i inkrementy (I)	RD
RC	2,42
RH	1,10
RO (grupa karbonylowa)	2,21
RO (eter)	1,64
RO (grupa hydroksylowa)	1,53
RCl	5,97
I (wiązanie podwójne)	1,73
I (wiązanie potrójne)	2,40

Tabela 1b.

Refrakcje wiązań	RD
C-H	1,68
C-N	1,54
C-Cl	6,53
C-C	1,29
C=C	4,16
C-O	1,54
C=O	3,38
O-H (alkohole) O-H (kwasy)	1,66 1,80

Jeśli wyznaczymy refrakcję molową związku o znanym wzorze sumarycznym, możemy zaproponować kilka struktur odpowiadających określonemu składowi chemicznemu i korzystając z wartości refrakcji atomów i inkrementów lub wiązań obliczyć refrakcje teoretyczne. Wartość najbliższa wartości doświadczalnej pozwoli na ustalenie struktury badanego połączenia.

Addytywność refrakcji pozwala również na wyznaczanie składu mieszaniny substancji. Jeśli wzajemne oddziaływania składników roztworu nie zmieniają w istotny sposób polaryzowalności ich cząsteczek, to refrakcje składników są addytywne:

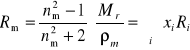
(24)

gdzie n_m jest współczynnikiem załamania mieszaniny (roztworu),

n_i jest współczynnikiem załamania czystego składnika,

R_m jest refrakcją molową mieszaniny,

R_i jest refrakcją czystego składnika,

ρ_m jest gęstością mieszaniny,

x_i jest ułamkiem molowym składnika w roztworze,

M_m
, przy czym M_i oznacza masę molową składnika, x_i jego ułamek molowy w układzie.

Dla układu dwuskładnikowego otrzymamy:

(25)

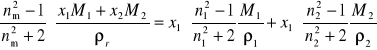
(26)

Podstawiając
, z równania (26) obliczamy ułamek molowy
składnika roztworu.

Skład roztworu dwuskładnikowego możemy również wyznaczyć na podstawie refrakcji właściwej roztworu

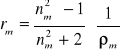
(27)

i refrakcji właściwych składników roztworu:

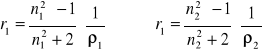
(28)

Z addytywności refrakcji wynika, że

(29)

Podstawiając równania (27) i (28) do równania (29) możemy wyliczyć ułamek molowy.

Zagadnienia do opracowania.

1. Moment dipolowy trwały i indukowany. Związek momentu dipolowego ze strukturą cząsteczki.

2. Przenikalność elektryczna i współczynnik załamania światła.

3. Polaryzacja orientacyjna, atomowa i elektronowa. Wpływ częstości zmiennego pola elektrycznego na polaryzację.

4. Równanie Debye'a i metody wyznaczania momentu dipolowego substancji w fazie gazowej i ciekłej.

5. Refrakcja molowa, addytywność refrakcji, związek między refrakcja a strukturą cząsteczki, refrakcja mieszaniny i wyznaczanie składu mieszaniny na podstawie refrakcji.

Literatura

1. Atkins P. W.: Podstawy chemii fizycznej, PWN, Warszawa1999, s. 429 - 465.

2. Atkins P. W.,: Chemia fizycznaj, PWN, Warszawa 2001, s. 627 - 638.

3. Pigo* K., Ruziewicz Z.: Chemia fizyczna, PWN, Warszawa 1980, s. 623 - 638.

Aparatura

Refraktometr, densytometr, szkło laboratoryjne.

Odczynniki

Toluen, aceton, chloroform, alkohol butylowy, alkohol benzylowy, czterochlorek węgla.

Wykonanie ćwiczenia

1. Za pomocą refraktometru wyznaczyć współczynniki załamania kilku cieczy organicznych (toluen, aceton, chloroform, alkohol butylowy, alkohol benzylowy, czterochlorek węgla) oraz mieszaniny dwóch substancji o nieznanym składzie (np. acetonu i butanolu). Dla badanej mieszaniny wyznaczyć gęstość za pomocą densytometru.

2. Zmierzyć współczynnik załamania n_x oraz gęstość cieczy organicznej, ρ_x o wzorze sumarycznym C₄H₈O₂.

3. Wyniki pomiarów przedstawić w tabeli:

Rodzaj substancji	n	ρ [g/cm^3]	M [g/mol]

Opracowanie wyników

1. Na podstawie wyników pomiarów współczynników załamania świa­t*a obliczyć refrakcje molowe toluenu, cztero­chlorku węgla, acetonu, chloroformu i alkoholu butylowego. Porównać je z wartościami obliczonymi na podstawie refrak­cji atomów i inkrementów (
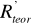
   ) (tabela 1a) i refrakcji wiązań (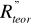
   ) (tabela 1b). Gęstość badanych sub­stan­cji znaleźć w tablicach fizykochemicznych. Wyniki obliczeń zestawić w tabeli:

Rodzaj substancji

2. Korzystając ze zmierzonych wartości n_x i ρ_x nieznanego związku obliczyć jego refrakcję molową. Zaproponować moż­liwe wzory strukturalne dla kwasu, estru i eteru o wzorze C₄H₈O₂. Obliczyć teoretyczne refrakcje molowe połączeń o zaproponowanej strukturze na podstawie refrakcji atomów i inkrementów oraz wiązań, a następnie po­ró­wnać je z wartością doświadczalną w celu potwierdzenia stru­ktury ba­da­nego związku.

3. Obliczyć refrakcję właściwą mieszaniny acetonu i butanolu r_m oraz refrakcje właściwe czystych składników roztworu
i
. Obliczyć ułamki molowe obu składników w mieszaninie.

4. Znając ułamki molowe wyznaczyć skład mieszaniny w % wagowych (
oraz
) korzystając ze wzorów:




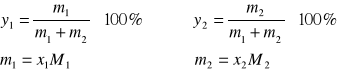
Dyskusja wyników

1. Przedstawić sens fizyczny refrakcji molowej. Jakich informacji o właściwościach cząsteczek dostarcza nam porównanie wartości refrakcji dla różnych związków organicznych?

2. Ocenić zgodność doświadczalnych i teoretycznych wartości refrakcji dla badanych związków. Czy wyznaczenie refrakcji molowej pozwala na identyfikację struktury chemicznej?

3. Przedstawić metodę wyznaczania składu mieszaniny w oparciu o wyznaczanie refrakcji.

2

r

-q

+q

1/T




---