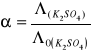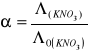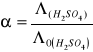Robert Maniura

Sprawozdanie z ćwiczenia nr 5: Przewodnictwo równoważnikowe elektrolitów.

1. 
   Wyniki ćwiczenia:

Temperatury roztworów 18⁰C.

2. Wstęp teoretyczny:

Szczególnym rodzajem roztworu ciekłego jest ten, w którym cząsteczki rozpuszczone, czy też agregaty tworzące się wokół nich, są naładowane elektrycznie i tworzą jony. Roztwory takie przewodzą prąd elektryczny, a z jego przepływem związana jest elektroliza, czyli wydzielanie się substancji na elektrodach na skutek rozładowania się na nich jonów. Roztwory takie nazywamy roztworami elektrolitów. Substancje, które przy rozpuszczaniu w danym rozpuszczalniku tworzą takie roztwór, nazywamy elektrolitami.

Fundamentalnym zjawiskiem odróżniającym roztwory elektrolitów od innych roztworów jest, jak już powiedziane było wcześniej, ich przewodnictwo jonowe i zjawisko elektrolizy. Podstawowymi prawami elektrolizy są prawa Faradaya, określające związek między ładunkiem elektrycznym, który przepłynął przez roztwór, a wydzieloną na elektrodach masą substancji.

Ładunek
(gdzie
to liczba Faradaya równa
) rozładowuje jeden gramorównoważnik chemiczny jonów. Jeżeli wartościowość jonu jest różna od jedności i wynosi na przykład
, to wówczas dla rozładowania jednego mola takich jonów potrzeba ładunku wynoszącego
kulombów. Przez równoważnik elektrochemiczny
danego jonu rozumiemy liczbę gramów wydzielonych przez przepływ 1 kulomba. Stąd

gdzie
jest masą jednego mola jonów.

Zgodnie z tym, jeżeli wartościowość jonów wynosi
i jeżeli przez roztwór przepływa prąd o natężeniu
przez czas
, wówczas liczba moli wydzielonej substancji wyniesie

stąd na wydzieloną masę otrzymamy wzór
czyli, znane prawo Faradaya ma postać

Prawo to mówi, że masa danej substancji, ulegającej na elektrodzie, jest proporcjonalna do ładunku, jaki przepłynął przez obwód, oraz że masy różnych substancji ulegających reakcji na elektrodach przy przepływie danego ładunku są proporcjonalne do ich równoważników elektrochemicznych.

Prawo Faradaya w postaci

służy jako podstawa definicji jednostki natężenia prądu, ampera. Ta metoda oznaczania wielkości ładunku przepływającego w obwodzie nosi nazwę kulometrii.

W czasie elektrolizy naładowane jony doznają w polu elektrycznym działania siły. Siła ta jest zależna od natężenia pola oraz od ładunku jonu. Dzięki jej działaniu jon uzyskuje pewne przyspieszenie w kierunku linii pola. Przyspieszenie to jest oczywiście odwrotnie proporcjonalne do masy jonu. Zauważmy jednak, że jon, tak jak wszystkie cząstki w roztworze, podlega bezwładnym ruchom cieplnym. W rezultacie zatem działania pola elektrycznego wykazuje on pewną dodatkową składową ruchu wzdłuż linii pola. Dzięki niej jony poruszają się w polu elektrycznym płynąc w roztworze ku elektrodom.

Ruchowi temu przeciwstawia się opór ośrodka. Opór ten zależy od szeregu czynników, przede wszystkim od struktury bliskiego zasięgu, w jakiej tkwi jon, od sił wzajemnych oddziaływań, a zatem od stężenia, od wielkości samego jonu, od lepkości roztworu itp. Opór ten wzrasta szybko wraz z prędkością jonu, tak że jego ruch staje się prawie natychmiast po włączeniu pola ruchem jednostajnym.

Prędkość zatem, z jaką poruszać się będzie jon wzdłuż linii pola, będzie zależeć od natężenia pola, ładunku jonu, jego masy, a również od temperatury, rodzaju ośrodka, stężenia, lepkości, wielkości jonu.

Doświadczenie uczy, że w tych warunkach roztwory elektrolitów stosują się do prawa Ohma.

Ponieważ gęstość prądu, a więc ładunek przepływający w jednej sekundzie przez przekrój 1 cm², prostopadły do kierunku prądu, jest równa iloczynowi liczby jonów w 1 cm³ i ich prędkości w kierunku pola, a liczba jonów nie zależy od natężenia prądu, przeto ze stosowania się roztworów elektrolitów do prawa Ohma wynika, że prędkość jonów jest proporcjonalna do natężenia prądu.

Opierając się na proporcjonalności wprowadzamy pojęcie ruchliwości jonu. Rozumiemy przez nie bezwzględną wartość jego prędkości przy natężeniu pola równym jedności. Jest to wielkość charakterystyczna dla danego jonu.

Konsekwencją różnej ruchliwości różnych jonów jest, że w przenoszeniu ładunku w roztworze w czasie elektrolizy aniony i kationy biorą udział w różnym stopniu.

Ponieważ roztwór elektrolitu jako całość jest na zewnątrz elektrycznie obojętny i w każdym centymetrze sześciennym roztworu zachodzi równość ładunku obu znaków, przeto spełnione jest wszędzie równanie

stąd
a więc

Oczywiście
i
są na ogół różne, gdyż różne są na ogół
i
.

Ułamek całkowitego ładunku
, przepływającego przez przekrój 1 cm² w ciągu 1 sekundy, przenoszony przez dany rodzaj jonów, nazywamy za Hittorfem liczbą przenoszenia tych jonów. Zgodnie z tą definicją liczby przenoszenia kationów i anionów dane są równaniami

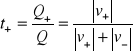
oraz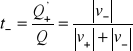
wynika z tej definicji, że

Z samej definicji liczb przenoszenia wynika, że nie są one wielkością charakterystyczną dla danego jonu, niezależnie od jego partnera. Wyrażają bowiem względne zdolności przenoszenia ładunku.

Na ogół wielkości liczb przenoszenia nie zależą silnie od stężenia roztworu. Szczególnie nieznaczna jest ta zależność u elektrolitów mocnych.

Jeśli chodzi o zależność wartości liczb przenoszenia od temperatury, to na ogół wzrastają one wraz ze wzrostem temperatury do wartości 0,5. nie jest to jednak regułą bezwzględnie obowiązującą.

Wzór na
podany powyżej podaje ładunek przepływający w ciągu 1 sekundy przez przekrój 1 cm² prostopadły do kierunku prądu. Wyraża on zatem gęstość prądu
. Niechaj natężenia pola wynosi
. Z definicji ruchliwości jonów wynika, że moduły prędkości jonów
i
dane są równaniami

oraz
gdzie
i
oznaczają ruchliwości kationu i anionu. Możemy zatem równanie na
napisać w postaci

Wobec stosowania się roztworów elektrolitów do prawa Ohma, możemy napisać również, że

gdzie
oznacza przewodnictwo właściwe roztworu.

Przyjmując, że pole w elektrolicie jest jednorodne, możemy ostatnie równanie napisać w postaci

gdzie
jest różnicą potencjałów między elektrodami a
odległością między nimi.

Jeżeli przekrój warstwy elektrolitu, poprzeczny do kierunku prądu, oznaczymy przez
, to wówczas natężenie prądu dane będzie wyrażeniem

stąd
czyli
gdzie
oznacza opór przewodzącej warstwy elektrolitu.

Przewodnictwo właściwe
jest oczywiście odwrotnością oporu właściwego

Różnice w przewodnictwie właściwym różnych elektrolitów mogą być podstawą tzw. miareczkowania konduktometrycznego.

Badania nad zależnością przewodnictwa właściwego roztworów elektrolitów od temperatury i od stężenia pozwoliły stwierdzić, że przewodnictwo to rośnie z temperaturą. Zachowuje się zatem odmiennie od przewodnictwa metali, które ze wzrostem temperatury maleje.

Inaczej przedstawia się zależność od stężenia. Gdy wychodzimy od stężeń bardzo małych, bliskich zeru, i zwiększamy je przewodnictwo właściwe elektrolitów początkowo rośnie, osiąga maksimum, po czym maleje (spowodowane to jest zmniejszeniem ruchliwości jonów, stałej dysocjacji, itp.).

Ta różnica pomiędzy przebiegiem zależności przewodnictwa od stężenia u elektrolitów słabych i mocnych zaznacza się szczególnie wyraźnie przy porównywaniu tzw. przewodnictw równoważnikowych. Przewodnictwo równoważnikowe jest to przewodnictwo wyrażone równaniem

gdzie
to przewodnictwo właściwe a
stężeniem wyrażonym w gramorównoważniku na jednostkę objętości. Przewodnictwo równoważnikowe rośnie z temperaturą, maleje natomiast ze stężeniem. Krzywa
odcina na osi rzędnych przy
pewną charakterystyczną dla danego elektrolitu wartość. Wartość tę nazywamy przewodnictwem równoważnikowym granicznym i oznaczamy symbolem
. Wyznaczenie tej wartości dla elektrolitów słabych nie jest doświadczalnie możliwe, gdyż przewodnictwo właściwe
staje się u nich, przy
, bardzo małe. Nie może być również zastosowana ekstrapolacja graficzna, gdyż przebieg krzywej
jest przy
tak stromy, że trudno jest określić
. U elektrolitów mocnych natomiast można wyznaczyć
dość dokładnie drogą ekstrapolacji. Jak się bowiem okazuje, zależność
od
, dla małych
, jest u tych elektrolitów dana równaniem
.

Kohlrausch zauważył, że wartości
różnych elektrolitów spełniają bardzo charakterystyczne prawidłowości. Jeślibyśmy obliczyli różnice wartości
dla par soli, różniących się albo wyłącznie kationem, albo wyłącznie anionem, to zauważylibyśmy, że różnice te są stałe. Ta prawidłowość nasunęła Kohlrauschowi myśl, że widocznie w rozcieńczeniu nieskończenie wielkim kationy i aniony biorą udział w przewodzeniu prądu zupełnie niezależnie od siebie. Innymi słowy, że przewodnictwa równoważnikowe graniczne składają się addytywnie z wielkości charakterystycznych dla poszczególnych jonów

Przy takiej addytywności granicznych przewodnictw równoważnikowych poszczególnych jonów, czyli niezależnego przewodzenia jonów w rozcieńczeniu granicznym, stosunek przewodnictwa równoważnikowego granicznego danego jonu do przewodnictwa równoważnikowego granicznego soli będzie równy liczbie przenoszenia tego jonu w rozcieńczeniu granicznym

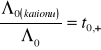
oraz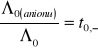

stąd ze znalezionych doświadczalnie
,
,
można obliczyć
.

Znając
dla poszczególnych jonów elektrolitów mocnych można obliczyć
dla elektrolitów słabych. W rozcieńczeniu nieskończenie wielkim równowaga dysocjacji tych elektrolitów jest oczywiście całkowicie przesunięta w stronę jonów, tak że można przyjąć ich pełną dysocjację, a stąd również niezależność przewodzenia jonów.

Jak już było wspomniane, przewodnictwo równoważnikowe wzrasta wraz z temperaturą. Jeśli roztwór elektrolitu nie jest nieskończenie rozcieńczony a elektrolit nie jest mocny, wzrost ten powodowany jest wzrostem zarówno dysocjacji jak i ruchliwości. Jeżeli elektrolit jest mocny lub roztwór jest nieskończenie rozcieńczony, wzrost ten powodowany jest wyłącznie wzrostem ruchliwości.

Prócz temperatury wpływ na ruchliwość jonów, a tym samym i na przewodnictwo równoważnikowe, ma rodzaj rozpuszczalnika.

Zjawiska elektrolitycznego przewodzenia prądu spotykamy nie tylko w roztworach wodnych i niewodnych. Można je obserwować również w stopionych związkach heteropolarnych.

3. Opracowanie wyników:

Wyznaczam stałą naczyńka.

Stężenie roztworu KCl [mol/l]	Przewodnictwo właściwe (doświadczalne) [S/cm]	Przewodnictwo właściwe (teoretyczne) [S/cm]	Stała naczyńka	Stała naczyńka (wartość średnia)
0,1	0,01237	0,01213	0,980598222	0,966576449
0,01	0,001395	0,001329	0,952688172
0,001	0,000149	0,000144	0,966442953

Obliczam przewodnictwo równoważnikowe, stężenie wyrażone w gramorównoważnikach na jednostkę objętości oraz pierwiastek z tego stężenia.

Dla K₂SO₄.

nr	Objętość K2SO4 o stężeniu 0,02 mol/l [cm^3]	Stężenie wyrażone w gramorównoważnikach na jednostkę objętości [g-równ/l]	Pierwistek ze stężenia	Przewodnictwo właściwe (zmierzone) [S/cm]	Przewodnictwo równoważnikowe (wyliczone) [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]
1	0,25	0,0001	0,01	0,00002	200
2	0,5	0,0002	0,014142136	0,000039	195
3	0,75	0,0003	0,017320508	0,000051	170
4	1,25	0,0005	0,02236068	0,000083	166
5	2	0,0008	0,028284271	0,000124	155
6	3	0,0012	0,034641016	0,000185	154,1666667
7	4	0,0016	0,04	0,000244	152,5

Dla KNO₃.

nr	Objętość KNO3 o stężeniu 0,02 mol/l [cm^3]	Stężenie wyrażone w gramorównoważnikach na jednostkę objętości [g-równ/l]	Pierwistek ze stężenia	Przewodnictwo właściwe (zmierzone) [S/cm]	Przewodnictwo równoważnikowe (wyliczone) [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]
1	0,25	0,00005	0,007071068	0,00001	200
2	0,5	0,0001	0,01	0,000019	190
3	0,75	0,00015	0,012247449	0,000028	186,6666667
4	1,25	0,00025	0,015811388	0,000045	180
5	2	0,0004	0,02	0,00007	175
6	3	0,0006	0,024494897	0,000099	165
7	4	0,0008	0,028284271	0,000131	163,75

Dla H₂SO₄.

nr	Objętość H2SO4 o stężeniu 0,02 mol/l [cm^3]	Stężenie wyrażone w gramorównoważnikach na jednostkę objętości [g-równ/l]	Pierwistek ze stężenia	Przewodnictwo właściwe (zmierzone) [S/cm]	Przewodnictwo równoważnikowe (wyliczone) [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]
1	0,25	0,0001	0,01	0,000042	420
2	0,5	0,0002	0,014142136	0,000082	410
3	0,75	0,0003	0,017320508	0,000119	396,6666667
4	1,25	0,0005	0,02236068	0,000197	394
5	2	0,0008	0,028284271	0,000306	382,5
6	3	0,0012	0,034641016	0,000445	370,8333333
7	4	0,0016	0,04	0,000593	370,625

Wyznaczam przewodnictwo równoważnikowe graniczne metodą ekstrapolacji i obliczam stałą dysocjacji poszczególnych elektrolitów.

Elektrolit	Przewodnictwo równoważnikowe graniczne wyznaczone metodą ekstrapolacji [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]
K2SO4	208,74
KNO3	208,34
H2SO4	431,75

nr	Przewodnictwo równoważnikowe [S*cm^2*mol^-1] lub [W^-1*cm^2*mol^-1]	Stała dysocjacji	Przewodnictwo równoważnikowe [S*cm^2*mol^-1] lub [W^-1*cm^2*mol^-1]	Stała dysocjacji	Przewodnictwo równoważnikowe [S*cm^2*mol^-1] lub [W^-1*cm^2*mol^-1]	Stała dysocjacji
1	200	0,958129731	200	0,959969281	420	0,972785177
2	195	0,934176487	190	0,911970817	410	0,949623625
3	170	0,814410271	186,6666667	0,895971329	396,6666667	0,918741556
4	166	0,795247677	180	0,863972353	394	0,912565142
5	155	0,742550541	175	0,839973121	382,5	0,885929357
6	154,1666667	0,738558334	165	0,791974657	370,8333333	0,858907547
7	152,5	0,73057392	163,75	0,785974849	370,625	0,858425014

Znając wartość tablicową jednego z jonów obliczam pozostałe wartości (odczytałem z tablicy przewodnictwo równoważnikowe graniczne jonu
-
).

Dla H₂SO₄:

Dla K₂SO₄:

Dla KNO₃:

Porównanie wyników z wartościami tablicowymi:

nr	Przewodnictwo równoważnikowe (tablicowe) [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]	Przewodnictwo równoważnikowe (obliczone) [S*cm^2*mol^-1] lub [^-1*cm^2*mol^-1]	Błąd procentowy
	73,5	126,79	72,52%
	80,0	81,95	2,375%
	71,46	81,55	14,05%

4. Wnioski:

Błędy, które wynikły podczas doświadczenia spowodowane są niedokładnością rozcieńczania roztworów elektrolitów oraz niedokładnym wypłukaniem elektrody po każdorazowym pomiarze. Wszystkie obliczenia wykonane do sprawozdania wykazują jednak, że można z nich stworzyć wykresy nie odbiegające od ogólnie przyjętej zasady, że wykresy przewodnictwa równoważnikowego elektrolitów pokazują spadek tegoż przewodnictwa wraz ze wzrostem stężenia.

5. Wykresy:

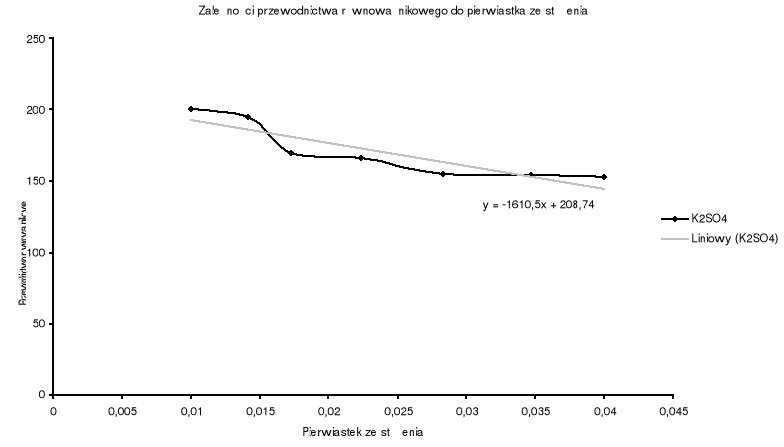
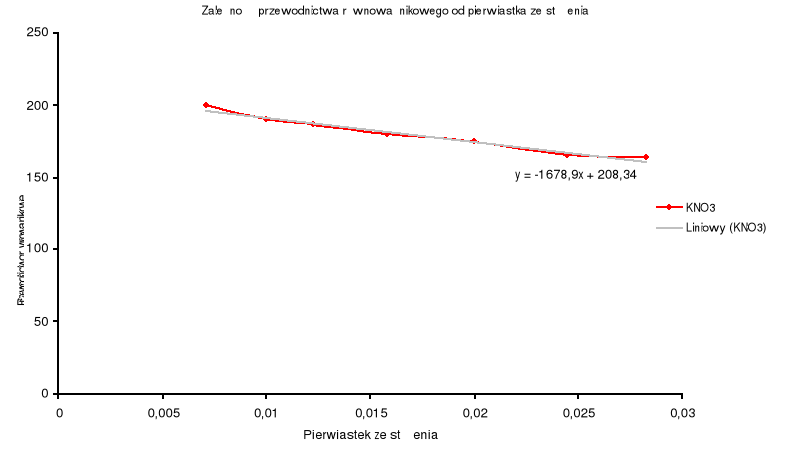
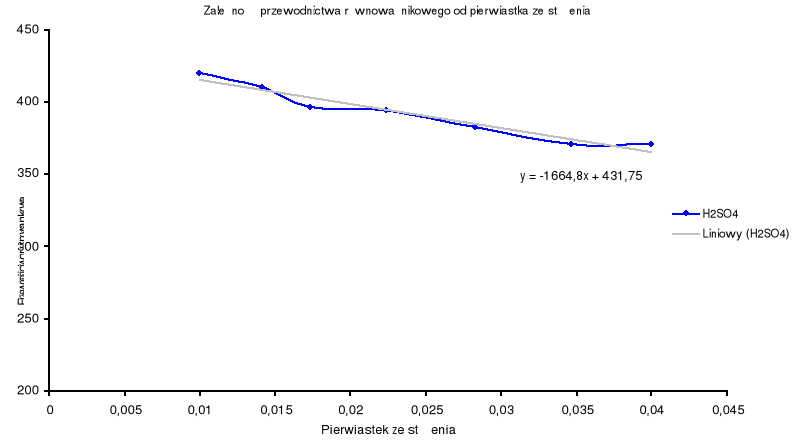
6. Literatura:

Kazimierz Gumiński „Wykłady z chemii fizycznej”.

7

Stężenie roztworu KCl w [mol/l]	Przewodnictwo właściwe KCl [S/cm]
0,1	12,37
0,01	1,395
0,001	0,149

nr	Objętość elektrolitu o stężeniu 0,02 mol/l w [cm^3]	Przewodnictwo właściwe K2SO4 [S/cm]	Przewodnictwo właściwe KNO3 [S/cm]	Przewodnictwo właściwe H2SO4 [S/cm]
1	0,25	0,020	0,010	0,042
2	0,50	0,039	0,019	0,082
3	0,75	0,051	0,028	0,119
4	1,25	0,083	0,045	0,197
5	2,00	0,124	0,070	0,306
6	3,00	0,185	0,099	0,445
7	4,00	0,244	0,131	0,593

---