Wydział: FTiMK	Imie i Nazwisko: Marcin Wiśniowski	Nr. Zepołu 8	Ocena Ostateczna
Grupa: Trzecia	Tytół ćwiczenia: Wyznaczanie modułu Younga metodą rozciągania drutu i strzałki ugięcia pręta	Nr. Cwiczenia 4	Data Wykonania: 23.11.2001

1. Wprowadzenie

Przyjmijmy, że na pręt (drut) o przekroju kołowym i długości pierwotnej l działa osiowa siła rozciągająca F. Pręt wydłuży się wówczas o Δl przyjmując długość l₁ Wielkość Δl = l₁ - l nazywamy wydłużeniem bezwzględnym.

Wydłużeniem jednostkowym lub względnym ε (a ogólniej odkształceniem) pręta nazywamy stosunek przyrostu długości do jego długości początkowej i oznaczamy je:

ε = Δl / l

Ciśnienie lub w przypadku rozciągania pręta naprężenie o określamy jako stosunek siły rozciągającej F do powierzchni przekroju poprzecznego pręta S:

σ = F / S

Badania zależności naprężenia od odkształcenia wykazały, że dla niewiel­kich odkształceń naprężenia są wprost proporcjonalne do odkształceń. Jest to tzw. prawo Hooke'a. Można je zapisać:

σ = Eε

gdzie E jest stałą dla danego mate­riału] nazywaną modułem Younga lub współczynnikiem sprężystości wzdłużnej.

W szerszym zakresie odkształ­ceń, zależność naprężeń od od­kształceń dla stali (ma przebieg podobny do przedsta­wionego na rysunku. Wyróżniamy tu kilka obszarów: OA - obszar proporcjonalnego wzrostu naprężeń do odkształceń, w którym spełnione jest prawo Hooke'a. W obszarze AB odkształcenia są jeszcze sprężyste, tzn. po usunięciu naprężenia odkształce­nie wraca do zera, lecz nie zachodzi tu już proporcjonalność. Obszar BC, pra­wie równoległy do osi odciętych, w którym materiał staje się podobny do ciasta i potocznie mówimy, że „płynie"; jest to tzw. obszar plastyczności. W obszarze tym wywiązuje się sporo ciepła na skutek przesuwania się wzajemnego mikro-kryształów materiału, a uprzednio wypolerowana powierzchnia pręta staje się matowa. Powyżej punktu C materiał czyni jak gdyby ostatni wysiłek, aby się oprzeć siłom rozrywającym, następuje znów wzrost naprężeń. W punkcie D naprężenie osiąga największą wartość, czyli granicę wytrzymałości. Tu mate­riał przestaje się wydłużać równomiernie tak, że w pewnym punkcie powstaje tzw. „szyjka", czyli miejscowe przewężenie. Przy ciągłym odkształcaniu na­prężenia spadają, krzywa zagina się i następuje zerwanie (punkt D').

2. Metoda pomiaru

• Wyznaczanie modułu Younga przez rozciągnięcie drutu

Jeden koniec stalowego drutu o długości około dwu metrów jest zamoco­wany w uchwycie górnego wspornika osadzonego w ścianie. Do dolnego końca drutu jest przytwierdzona ciężka ramka stalowa wsparta na czujniku mikrometrycznym, podtrzymywanym przez uchwyt dol­nego wspornika osadzonego w ścianie. Ramka wstępnie napina i prostuje drut. Do ram­ki podwieszona jest szalka na odważniki. Czuj­nik mikrometryczny pozwala mierzyć przyrosty długości A/ z dokładnością 0,005 mm.

Czujnik jest tak skonstruowany, że możliwe jest przed przystąpieniem do pomiarów napro­wadzenie jego wskazówki na zero skali. Po wy­konaniu tej czynności (wyzerowaniu), będziemy kładli na szalkę ciężary F i odczytywali przyro­sty długości Δl.

• Wyznaczanie modułu Younga przez pomiar strzałki ugięcia pręta

Stosunkowo prostą metodą jest wyznaczenie modułu Younga przez pomiar tzw. Strzałki ugięcia. Jest to wielkość przesunięcia swobodnego końca pręta z jednej strony sztywno zamocowanego w uchwycie i poddanego na drugim koń­cu działaniu siły F prostopadłej do jego długości

Dla pręta o przekroju prostokątnym, długości l (mierzonej od uchwytu), szero­kości d i grubości h, według teorii sprężystości strzałka ugięcia Y jest równa:

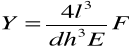
Wzór ten można stosować dla pręta wykonanego z materiału jednorodnego i izotropowego oraz w przypadku promieni krzywizny dużych w porównaniu z jego długością. Wyznaczając zależność strzałki ugięcia Y od wartości siły F można obliczyć współczynnik a nachylenia prostej Y=f(F), który jest współ­czynnikiem proporcjonalności we wzorze

A moduł Younga wynosi:

3. Tabele pomiarowe i obliczenia.

• Wyznaczanie modułu Younga przez rozciąganie drutu

Lp	1	2	3	4	5	6	7	8	9	10
d (mm)	0,6	0,61	0,6	0,61	0,61	0,6	0,6	0,61	0,6	0,6
l = 3,032 m

g = 9,8105 [m/s²]

Lp	m	F = mg	Δl
	kg	N	mm	m
1	0,5	4,9052	0,35	0,350 · 10^-3
2	1	9,8105	0,525	0,525 · 10^-3
3	1,5	14,7157	0,775	0,775 · 10^-3
4	2	19,6210	1,02	1,020 · 10^-3
5	2,5	24,5262	1,34	1,340 · 10^-3
6	3	29,4315	1,53	1,530 · 10^-3

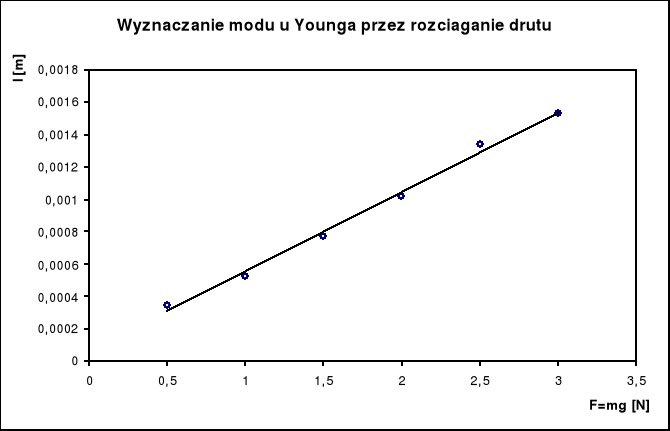
Sporządzam wykres zależności przyrostu długości Δl od siły wydłużającej F. Jeżeli przy obciążaniu drutu nie przekroczyliśmy granicy stosowalności prawa Hooke'a, punkty pomiarowe powinny układać się na prostej y = ax + b wychodzącej z początku układu.

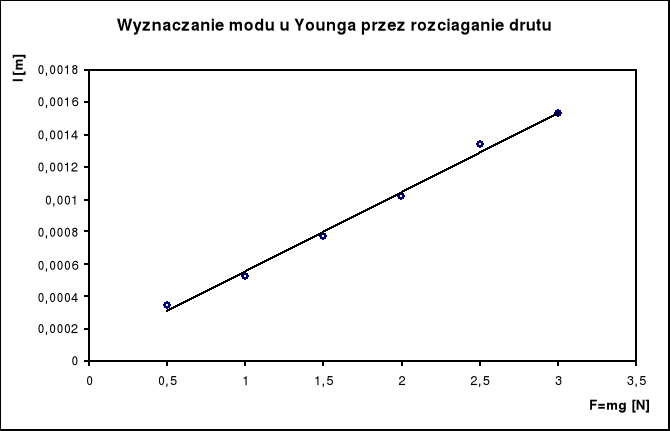
Korzystając ze wzorów na regresję liniową:

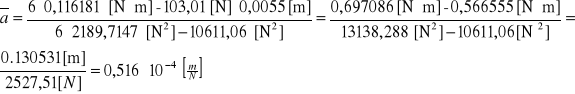
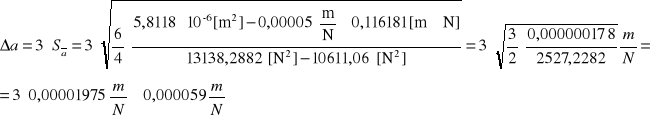
Wyznaczam moduł Younga dla przyłożonej masy równej 3 [kg]

Ponieważ

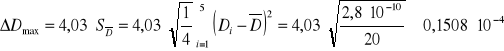
[m]

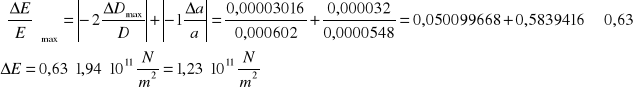
Ostatecznie wartość modułu Younga wyznaczona przez rozciąganie drutu wynosi:

E = (1,78 ± 1,23) ⋅ 10¹¹

• Wyznaczanie modułu Younga przez pomiar strzałki ugięcia pręta

Lp	1	2	3	4	5	6	7	8	9	10
d[mm]	19,69	19,64	19,65	19,61	19,79	19,67	19,67	19,73	19,73	19,67
h[mm]	6,01	6,09	6,08	6,03	6,06	6,12	6,00	6,04	6,03	6,03
l = 0,92 [m] ± 0,005 [m] s = 0,142 [m] ± 0,005[m]

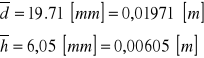
Lp	m	F=mg	Y'		Y
		kg	N	mm	m
1	0,05	0,4905	2	0,002	0,0016
2	0,10	0,9810	3	0,003	0,0024
3	0,15	1,4715	5	0,005	0,0040
4	0,20	1,7621	8	0,008	0,0064
5	0,25	2,4526	10	0,010	0,0080
6	0,30	2,9431	12	0,012	0,0096
7	0,35	3,4336	14	0,014	0,0112
8	0,40	3,9242	16	0,016	0,0128
9	0,45	4,4147	18	0,018	0,0144
10	0,50	4,9052	20	0,020	0,0160

Korzystając ze wzorów na regresję liniową:

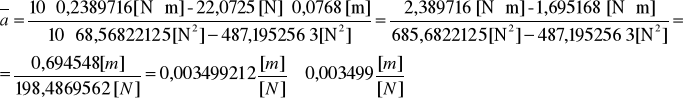
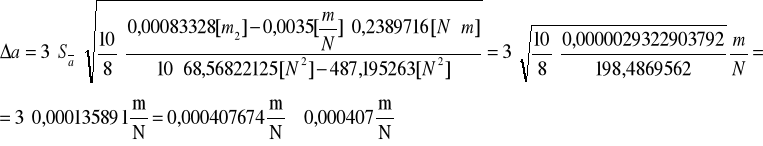
Wyliczony ze wzoru moduł Younga wynosi:

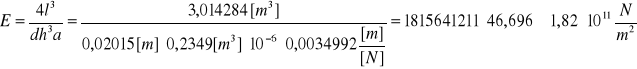
[m]

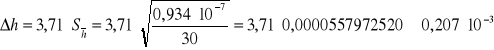
[m]

0,0238 + 0,1006 = 0,2423

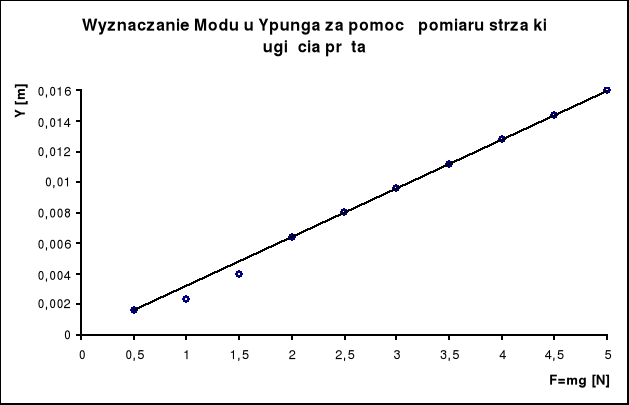
Ostatecznie wartość modułu Younga wyznaczona przez pomiar strzałki ugięcia pręta wynosi:

E= ( 1,81
0,44) ⋅ 10¹¹

4. Wnioski

Z przeprowadzonego doświadczenia wnioskuje że otrzymane w wyniku pomiarów wyniki sa zbliżone do tablicowych. Analizując wyniki stwierdzam że metoda pomiaru strzałki ugięcia pręta jest dokładniejsza o jeden rząd niepewności pomiarowej

wartość modułu Younga wyznaczona przez rozciąganie drutu wynosi:

E = (1,78 ± 1,23) ⋅ 10¹¹

Wartość modułu Younga wyznaczona przez pomiar strzałki ugięcia pręta wynosi:

E= ( 1,81
0,44) ⋅ 10¹¹

3

---