Celem ćwiczenia jest dobór nastaw regulatora typu PI znajdującego się w układzie sterowania pewnym obiektem dynamicznym.

Układ musi posiadać:

- czas regulacji poniżej 5 s

- zapas modułu co najmniej 16 dB

- zapas fazy co najmniej 30 stopni

- pasmo przenoszenia o pulsacji granicznej co najmniej 1 rad/s

Schemat blokowy układu:

1. Licznik i mianownik transmitancji obiektu regulacji.

Lo=conv([0.05 1],[0.05 1])

M=conv([1 5 17],conv([7 1],[0.01 1]))

Wynik:

L=[0.0025 0.1000 1.0000]

M=[0.0700 7.3600 37.2400 124.1700 17.0000]

2. Wykreślenie charakterystyki Bodego dla obiektu regulacji.

Charakterystyka Bodego dla układu regulacji ( co odpowiada charakterystykom układu otwartego z regulatorem P o wzmocnieniu kp=1)

margin(L,M)

Wykres 1 : Wyznaczenie zapasu modułu dla układu otwartego

Gm=62,3dB

Pm=∞

Lz, Mz dla transmitancji układu zamkniętego bez regulatora

[Lz,Mz]=cloop(L,M,-1)

Wynik:

Lz = 0 0 0.0025 0.1000 1.0000

Mz = 0.0700 7.3600 37.2425 124.2700 18.0000

step(Lz,Mz)

Uzyskany czas regulacji to 26 sec, dużo za dużo, więc dokładam regulator o parametrach wyznaczonych metodą Z-N

Określenie wzmocnienia granicznego/oscylacji (układ na granicy stabilności):

dM=20Log(k)= 62,3 (wyznaczony k -zapas modułu, pierwszy wykres)

k_osc =10^3.15=1.3032*10³ (k_osc=10^(dM/20))

3. Licznik i mianownik transmitancji obiektu i regulatora P ze wzmocnieniem k_osc

[Lz,Mz]=cloop(k_osc*Lo,Mo,-1)

(transmitancja układu zamkniętego o wzmocnieniu k_osc z regulatorem P)

Wynik:

Lz = 1.0e+003 * (0 0 0.0033 0.1303 1.3032)

Mz = 1.0e+003 * (0.0001 0.0074 0.0405 0.2545 1.3202)

4. Określenie okresu oscylacji graniczny

step(Lz,Mz,linspace(0,10))

(Odpowiedź układu z zamkniętą pętlą sprzężenia na skok jednostkowy, z tego wykresu wyznaczam T_osc dla Z-N)

Wykres 2: Charakterystyka skokowa dla układu zamkniętego.

Wynik odczytany z wykresu: T_osc=9,13-0,604 / 8=1.0658 s

5. Określenie nastaw regulatora PI wg. Zieglera-Nicholsa.

kp=0.45*kosc

ti=0.85*tosc

Wynik:

kp=586,4251

ti=0.9059 = (0,85 Tosc)

6. Licznik i mianownik transmitancji regulatora PI

Lr=kp*[ti 1]

Mr=[ti 0]

Wynik:

Lr = 178.2486 123.0697

Mr = 1.4484 0

7. Licznik i mianownik transmitancji układu otwartego z regulatorem PI

Lc=conv(Lr,L)

Mc=conv(Mr,M)

Wynik:

Lc = 0.4456 18.1325 190.5555 123.0697

Mc = 0.1014 10.6599 53.9367 179.8421 24.6220 0

8. Wykreślenie charakterystyki Bodego dla układu otwartego z regulatorem PI

margin(Lc,Mc)

Wykres 3: Charakterystyka Bodego dla układu otwartego

Wartości odczytane z wykresu:

Gm=1,94dB

Pm=6,09

Chcemy uzyskać przesunięcie wykresu amplitudy w prawo

Wymagana korekta wzmocnienia= -18dB (minimalny zapas modułu założyłem 16 dB, dlatego przesuwamy charakterystykę o 16+1.94)

Kp= 0,45 kosc * x

Współczynnik przesunięcia wykresu amplitudy

x =10^(2-18)/20 = 0.158

9. Obliczenie nowej wartości transmitancji układu otwartego z regulatorem PI

Lr=k1*Lr

Lc=conv(Lr,L)

(Mc takie jak było)

W dalszej części zmieniam wartość Ti i kp poprzez zmianę współczynnika przy doborze tych nastaw w metodzie Z-N. Czas regulacji wyszedł mi troszkę większy od zakładanego. Pozostałe wyniki (przeregulowanie, pasmo) doskonałe.

10. Wykreślenie charakterystyki Bodego dla układu otwartego z regulatorem PI

Po zmianie licznika transmitancji układu:

margin(Lc,Mc)

Wykres 4 : Charakterystyka układu po zmianie kp.

Wyniki odczytane z wykresu:

- zapas wzmocnienia gm=18 dB

- zapas fazy pm=38,8 stopni

11. Licznik i mianownik transmitancji układu zamkniętego z regulatorem PI

[Lcz,Mcz]=cloop(Lc,Mc,-1)

12. Wykres odpowiedzi układu zamkniętego z regulatorem PI na skok jednostkowy

step(Lcz,Mcz,linspace(0,10))

Wykres 5: Badanie przeregulowania i czasu regulacji dla kryterium 3%

Wyniki odczytane z wykresu:

Czas regulacji: tr=5,39 s

Przeregulowanie: kappa=(ymax-yn)/yn=(1.25-1)/1=0.25 < 35%

13. Wykres Bodego dla układu zamkniętego z regulatorem PI

Zapas modułu uzyskaliśmy ponad 16dB

14. Pasmo przenoszenia układu

Bode(Lz,Mz,logspace(0,0.5))

Pulsację graniczną z wykresu odczytaliśmy 1,42rad/s

Wykres uzyskaliśmy dla Ti=1,3 * tosc
kp=0,6 * kosc * x

Pasmo przenoszenia to zakres częstotliwości, dla której charakterystyka amplitudowa M(ω) układu zamkniętego nie zmienia się o więcej niż 3 dB. Częstotliwość ωg ograniczająca to pasmo jest nazywana pulsacją graniczną układu. Pulsacja graniczna równa jest w przybliżeniu częstości ωm dla układu otwartego.

Wnioski:

• Metoda Zieglera-Nicholsa daje w dużej liczbie przypadków poprawne rezultaty doboru nastaw regulatorów PI. Jednak w naszym przypadku metoda ta nie dała poprawnych rozwiązań musieliśmy zmieniać jeszcze wzmocnienie i czas zdwojenia. Metodę tą potraktowaliśmy jako 1 przybliżenie poszukiwanych wartości

• Metoda Z-N umożliwia dobór nastaw regulatora bez znajomości modelu matematycznego obiektu.

• Znajomość matematycznego modelu pozwala przy zastosowaniu odpowiednich programów komputerowych na znaczne skrócenie czasu doboru nastaw regulatora PI oraz przeprowadzenie symulacji dla różnych wartości nastaw.

•Działanie P regulatora zapewnia realizację elementarnego celu regulacji tj. zmniejszenie uchybu regulacji, jednak jest działaniem dość ryzykownym, ponieważ zmniejsza zapasy stabilności układu. Wykorzystaliśmy to by określić granice stabilności układu. Z wzoru na zapas modułu:
określiliśmy wzmocnienie k_osc, dla jakiego układ znajduje się na granicy stabilności, czyli chcieliśmy tak przesunąć charakterystykę Nyquista dla układu otwartego by przechodziła ona przez punkt(-1,0). Wtedy właśnie po zamknięciu pętli sprzężenia zwrotnego układ znajdzie się na granicy stabilności.

•Działanie regulatora I wprowadza efekt astatyzmu do układu regulacji umożliwiając minimalizację uchybu statycznego regulacji (w stanie ustalonym). Własności regulatora I wykorzystywaliśmy do zwiększania zapasu fazy w naszym układzie, czyli różnicę pomiędzy położeniem kątowym punktu przecięcia a kątem -180°. Parametry te czyli wzmocnienie oraz czas zdwojenia odpowiadają również za pozostałe wskaźniki jakości regulacji czyli pasmo przenoszenia układu, czas regulacji oraz przeregulowanie.

• Nie udało się zejść poniżej 5sec z czasem tr (5,39sec). Wyniki osiągnięte wyszły bardzo dobrze. Przeregulowanie 25 %, zapas modułu ponad 16 dB

4

Regulator PI

Obiekt regulacji

+

-

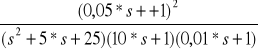
Zadana prędkość pochylania

Wielkość regulowana

---