Nr æw. 101	Data	Agata Sikorska	Wydział Elektryczny	Semestr II	Grupa E6
Prowadąca:			Przygotowanie	Wykonanie	Ocena

Temat: Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego.

1. Wahadło fizyczne

Wahadła fizyczne i matematyczne wykonują ruch drgający pod wpływem działającej siły ciężkości. W zakresie niedużych amplitud ruch ten jest ruchem harmonicznym, jego okres zależy od własności danego wahadła jak również od przyspieszenia ziemskiego.

Po wychyleniu z położenia równowagi na ciało działa moment siły ciężkości:
. Stosując II zasadę dynamiki do tej sytuacji otrzymamy:

(1), gdzie:

I - moment bezwładności ciała względem punktu zawieszenia A,

f - kąt wychylenia od położenia równowagi,

L - odległość od punktu zawieszenia A do środka ciężkości C.

Znak minus wskazuje, że moment siły zawsze stara się zmniejszyć wychylenie ciała.

2. Ruch harmoniczny

Ogólne równanie ruchu harmonicznego:

(2), gdzie jest prędkością kątową

Pamiętając, że kryterium harmoniczności ruchu opisanego równaniem (1) będzie spełnione tylko w zakresie małych wychyleń, dla których
. Porównując je z równaniem (2) otrzymujemy wyrażenie określające okres wahadła fizycznego:

(3), gdzie D=mgL jest momentem kierującym

3. Wahadło matematyczne

Wahadło matematyczne różni się tym od fizycznego, że cała masa układu jest skupiona w jednym punkcie (który jest oczywiście środkiem ciężkości). Połączenie pomiędzy środkiem ciężkości a punktem zawieszenia interpretuje się jako nieważką nić o długości l. Okres drgań takiego wahadła wyraża się wzorem:

(4)

4. Długość zredukowana wahadła fizycznego. Wahadło rewersyjne

Taka długość wahadła matematycznego, dla którego okresy drgań wahadła matematycznego i fizycznego są równe nazywa się długością zredukowaną wahadła fizycznego i wynosi ona:

(5)
Jeżeli znamy długość zredukowaną wahadła fizycznego, wówczas jego okres drgań możemy znaleźć za pomocą równania (4); nie jest do tego konieczna znajomość ani momentu bezwładności, ani momentu kierującego. Do wyznaczenia długości zredukowanej wahadła fizycznego wykorzystujemy tę jego własność, że wahadło zawieszone w punkcie A, a następnie w punkcie B posiada ten sam okres jeżeli odległość pomiędzy punktami zawieszenia jest długością zredukowaną.

Aby wykazać powyższą własność należy znaleźć warunki dla których możliwa jest równość okresów:

, (7), gdzie AB = l
Momenty bezwładności względem osi przechodzących przez punkty A i B można wyrazić przez moment
względem osi równoległej przechodzącej przez środek ciężkości (na podstawie twierdzenia Steinera):

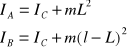
wówczas

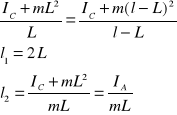
Wartość
odpowiada przypadkowi, gdy oba punkty zawieszone są symetrycznie względem środka ciężkości, natomiast
jest właśnie długością zredukowaną.

Specjalną postacią wahadła fizycznego jest wahadło rewersyjne lub odwracalne (rysunek obok). Na długim pręcie znajdują się dwa ciężarki w kształcie soczewek, które mogą być przesuwane wzdłuż pręta. Osie obrotu A i B mają postać pryzmatów metalowych i też mogą być przesuwane wzdłuż pręta.

5. Przebieg ćwiczenia

Wprowadzić w szczelinę czujnika fotoelektrycznego kulkę wahadła matematycznego. Uregulować jego długość tak, aby kreska na kulce była na jednym poziomie z kreską zaznaczoną na czujniku. Odczytać długość wahadła.

Wychylając wahadło o niewielki kąt zmierzyć czas 10 wahnięć. Obliczyć okres T wahadła matematycznego.

Pomiary powtórzyć co najmniej dla trzech różnych długości wahadła.

Znając okres T i długość wahadła matematycznego obliczyć przyspieszenie ziemskie.

Umocować ostrza A i B w odległości wzajemnej lr=0.8-1.1 m. Soczewkę 2 umocować w pobliżu końca wahadła.

Umocować soczewkę 1 w pobliżu ostrza B.

Zmierzyć czas około 10 wahnięć wahadła zawieszonego najpierw na ostrzu A, a następnie na ostrzu B. Obliczyć odpowiednie okresy TA i TB.

Zmieniając położenie soczewki 1 co 5 - 10 cm w całym zakresie między ostrzami 1 i 2 powtarzać pomiar okresów TA i TB.

Wykonać wykresy okresów TA i TB w funkcji położenia soczewki 1. Punkt przecięcia się krzywych TA i TB wyznacza okres T.

6. Pomiary dla wahadła matematycznego

czas 10 wachnięć [s]:

l.p.	l [m]	t = 10 T [s]	g [m/s^2]	Δg [m/s^2]
1	0,445	13,628	9,7941	0,02322
2	0,410	12,824	9,8154	0,02609
3	0,210	9,164	9,7827	0,03439

Z równania (4) otrzymujemy wzór na przyspiesznie ziemskie:




Otrzymujemy odpowiedni (dla kolejnych pomiarów):

1. 9,7941

2. 9,8154

3. 9,7827
   

Policzmy wartość średnią g:

Następnie liczymy odchylenie standardowe stosując współczynnik Studenta - Fishera dla 3 prób t_n=1,3:

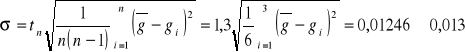
Ostatecznie, po zaokrągleniu: g = 9,797 ± 0,013 [m/s²]

7. Pomiary dla 10 wachnięć wahadła rewersyjnego w różnych położeniach soczewki nr 1;

L.p.	ls [m]	tA=10 TA [s]	tB=10 TB [s]
1	0,2	19,772	20,156
2	0,3	19,376	19,42
3	0,4	19,068	18,808
4	0,5	18,984	18,328
5	0,6	19,086	18,086
6	0,7	19,096	18,306
7	0,8	19,29	19,546
8	0,9	19,57	22,22

Otrzymujemy wykres:

Punkt przecięcia krzywych: t = 19,3 [s]
Daje to zgodnie ze wzorem analogicznym jak w poprzednim punkcie otrzymujemy:

Przyjmujemy dokładności pomiarów: Δl = 0,02 [m] i Δt = 0,001 [s]

8. Wnioski

Przeprowadzone doświadczenie udowodniło, że dokładniejszego pomiaru przyspieszenia można dokonać wahadłem matematycznym (ściślej--zbliżonym do matematycznego) niż wahadłem rewersyjnym.

Wyniki obu pomiarów są poprawne. Wpływ na dokładność pomiaru przyspieszenia za pomocą wahadła rewersyjnego ma również ma duża niedokładność miary wyskalowanej na pręcie. Wyniki pomiaru znacznie polepsza dokładne urządzenie mierzące okres.

---