Szeregi czasowe
Zmiany zjawisk w czasie prezentowane są w szeregach czasowych
Przykład 1:
Liczba Ludności Polski
rok |
liczba ludności na dzień 31 XII (w tys.) |
1995 |
38609,4 |
1996 |
38639,3 |
1997 |
38660 |
1998 |
38667 |
1999 |
38653,6 |
2000 |
38254 |
2001 |
38242,2 |
2002 |
38218,5 |
2003 |
38190,6 |
Źródło: www.stat.gov.pl
Jest to szereg czasowy momentów
Przykład 2:
Liczba urodzeń żywych w Polsce
Rok |
Urodzenia żywe |
1995 |
436312 |
1996 |
431211 |
1997 |
415166 |
1998 |
398103 |
1999 |
384379 |
2000 |
380476 |
2001 |
370247 |
2002 |
355526 |
2003 |
352785 |
Jest to szereg czasowy okresów.
Miary średnie w szeregach czasowych
Średnia arytmetyczna
- w szeregach okresów
- jest czuła na wartości odstające
Średnia chronologiczna
- w szeregach momentów
Średnia geometryczna
- dla zjawisk multiplikatywnych
- w szeregach z wartościami odstającymi
Średnia arytmetyczna
Średnia chronologiczna
Średnia geometryczna
Przykład:
Inflacja w Czechach od I do IX 2006 kształtowała się następująco:
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
2,9 |
2,8 |
2,8 |
2,8 |
3,1 |
2,8 |
2,9 |
3,1 |
2,7 |
Źródło: „Parkiet” 27.10.2006
Jaki był średni wskaźnik inflacji w tym okresie?
Przykład:
Skonsolidowane wyniki finansowe Swissmedu (przychody w mln zł):
Ikw. 2005 |
II kw. 2005 |
III kw. 2005 |
IV kw. 2005 |
I kw. 2006 |
2,91 |
3,05 |
2,81 |
3,3 |
3,64 |
Źródło: „Parkiet” 27.10.2006
Jakie średnie kwartalne przychody osiągał Swissmed w 2005 roku?
Przykład:
Liczba agentów pewnego towarzystwa ubezpieczeniowego na dzień 01 miesiąca:
Ikw. 2005 |
II kw. 2005 |
III kw. 2005 |
IV kw. 2005 |
I kw. 2006 |
238 |
265 |
315 |
276 |
280 |
Źródło: Dane umowne
Jaka jest średnia kwartalna liczba agentów współpracujących z tym towarzystwem?
Miary dynamiki
Przyrosty absolutne - pokazują bezwzględne zmiany poziomu zjawiska w dwóch porównywanych momentach lub okresach czasu:
- Przyrosty łańcuchowe
- Przyrosty jednopodstawowe
Przykład:
Liczba Ludności Polski
rok |
liczba ludności na dzień 31 XII (w tys.) |
przyrosty łańcuchowe |
przyrosty jednopodstawowe |
1995 |
38609,4 |
- |
0 |
1996 |
38639,3 |
29,9 |
29,9 |
1997 |
38660 |
20,7 |
50,6 |
1998 |
38667 |
7 |
57,6 |
1999 |
38653,6 |
-13,4 |
44,2 |
2000 |
38254 |
-399,6 |
-355,4 |
2001 |
38242,2 |
-11,8 |
-367,2 |
2002 |
38218,5 |
-23,7 |
-390,9 |
2003 |
38190,6 |
-27,9 |
-418,8 |
Indeksy indywidualne - pokazują względne zmiany poziomu zjawiska w dwóch porównywanych momentach lub okresach czasu, służą do badania zjawisk jednorodnych
- Indeksy łańcuchowe
- Indeksy jednopodstawowe
Przykład:
Liczba Ludności Polski
rok |
liczba ludności na dzień 31 XII (w tys.) |
indeksy łańcuchowe |
indeksy jednopodstawowe |
1995 |
38609,4 |
- |
1 |
1996 |
38639,3 |
1,000774 |
1,000774 |
1997 |
38660 |
1,000536 |
1,001311 |
1998 |
38667 |
1,000181 |
1,001492 |
1999 |
38653,6 |
0,999653 |
1,001145 |
2000 |
38254 |
0,989662 |
0,990795 |
2001 |
38242,2 |
0,999692 |
0,990489 |
2002 |
38218,5 |
0,99938 |
0,989876 |
2003 |
38190,6 |
0,99927 |
0,989153 |
Zamiana indeksów:
Łańcuchowych na jednopodstawowe
Jednopodstawowych na łańcuchowe
Przykład: Wskaźniki cen towarów i usług konsumpcyjnych w latach 1999-2006 w miesiącu styczniu)
|
Rok 1998 =100 |
1999 |
103,5 |
2000 |
113,9 |
2001 |
122,4 |
2002 |
126,9 |
2003 |
127,3 |
2004 |
129,6 |
2005 |
134,8 |
2006 |
135,7 |
O ile w każdym kolejnym roku różniły się ceny (jaki był roczny wskaźnik inflacji w kolejnych latach)?
Źródło: www.stat.gov.pl
Przykład:
(zamiana indeksów łańcuchowych na jednopodstawowe)
Dane umowne
Rok |
22000 |
2001 |
2002 |
2003 |
2004 |
2005 |
Rok pop. = 100 |
- |
135 |
130 |
125 |
120 |
115 |
Rok 2000 =100 |
|
|
|
|
|
|
Przykład: (zamiana indeksów jednopodstawowych na łańcuchowe)
Dane umowne
Rok |
22000 |
2001 |
2002 |
2003 |
2004 |
2005 |
Rok 2000 = 100 |
- 100 |
95 |
90 |
85 |
80 |
75 |
Rok pop. = 100 |
|
|
|
|
|
|
Tempo zmian (względny przyrost łańcuchowy) - pokazuje o ile procent poziom zjawiska wzrósł / zmalał w porównaniu do okresu poprzedniego
Przykład:
Liczba Ludności Polski
rok |
Liczba ludności na dzień 31 XII (w tys.) |
Indeksy łańcuchowe |
Indeksy jednopodstawowe |
Tempo zmian
|
1995 |
38609,4 |
- |
100,00% |
- |
1996 |
38639,3 |
100,08% |
100,08% |
0,08% |
1997 |
38660 |
100,05% |
100,13% |
0,05% |
1998 |
38667 |
100,02% |
100,15% |
0,02% |
1999 |
38653,6 |
99,97% |
100,11% |
-0,03% |
2000 |
38254 |
98,97% |
99,08% |
-1,03% |
2001 |
38242,2 |
99,97% |
99,05% |
-0,03% |
2002 |
38218,5 |
99,94% |
98,99% |
-0,06% |
2003 |
38190,6 |
99,93% |
98,92% |
-0,07% |
Średnie tempo zmian
Pokazuje średnią względną zmianę poziomu zjawiska z okresu na okres
Jest średnią geometryczną z indeksów łańcuchowych
Obliczanie średniego tempa z indeksów:
Przykład:
Liczba Ludności Polski
rok |
Liczba ludności na dzień 31 XII (w tys.) |
1995 |
38609,4 |
1996 |
38639,3 |
1997 |
38660 |
1998 |
38667 |
1999 |
38653,6 |
2000 |
38254 |
2001 |
38242,2 |
2002 |
38218,5 |
2003 |
38190,6 |
Średnie tempo wzrostu:
Średnie tempo spadku:
Indeksy agregatowe wielkości absolutnych
Służą do oceny zmian w czasie zjawisk niejednorodnych, które mogą być przedstawione wartościowo
Agregatowy indeks wartości
Agregatowe indeksy cen
Indeks cen Laspeyresa
Indeks cen Paaschego
Agregatowe indeksy ilości
Indeks ilości Laspeyresa
Indeks ilości Paaschego
Indeksy średnie
Indeks cen Fishera
Indeks ilości Fishera
Przykład: Obroty na GPW w Warszawie akcjami wybranych spółek
Spółka |
Ilość akcji 31 X |
Ilość akcji 15 XI |
Cena akcji 31 X (zł) |
Cena akcji 15 XI (zł) |
A |
3000 |
4700 |
12,5 |
14,2 |
B |
2350 |
2650 |
6,7 |
5,7 |
C |
9750 |
6800 |
5,5 |
5,5 |
|
|
|
|
|
(Dane umowne)
Zbadać wszechstronnie dynamikę zmian wartości obrotów na GPW akcjami tych spółek.
Strumienie
(szereg okresów)
Zasoby
(szereg momentów)
zjawiska
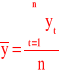
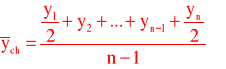
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wzrost poziomu zjawiska
Zjawisko pozostało na tym samym poziomie
Spadek poziomu zjawiska
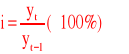
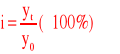
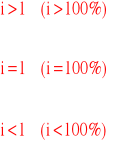
Wzrost poziomu zjawiska
Zjawisko pozostało na tym samym poziomie
Spadek poziomu zjawiska
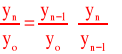
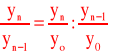
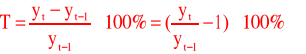
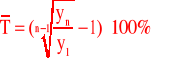
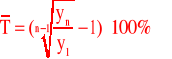
Indeks jednopodstawowy dla
n-tego okresu
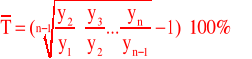
Iloczyn wszystkich indeksów łańcuchowych
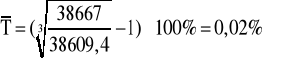
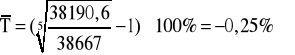
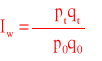
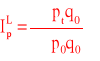
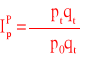
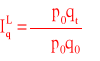
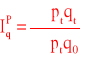
![]()
![]()
Wyszukiwarka
Podobne podstrony:
557
557
557
557
557
557
557
557
kodeks karny wykonawczy [Dz.U.97.90.557], Licencja Pracownika Ochrony
II CSK 557 12 1 id 209824 Nieznany
557
557
556 557
Szalikowcy – zmora polskiego futbolu [PDF, 557 KB]
więcej podobnych podstron