Politechnika Warszawska

Wydział Inżynierii Środowiska

Labolatorium nr 7
z Fizyki I:

Wyznaczanie energii promieniowania γ
za pomocą spektometru scyntylacyjnego

(#41)

Zespół (#15):

Dziuda Beata,

Król Zbigniew,

Kryczka Katarzyna.

Data wykonania: 14.IV.2000

Celem ćwiczenia było wyznaczenie energii promieniowania γ za pomocą spektometru scyntylacyjnego. Doświadczenie wspomagane było przez komputer.

Cząstki naładowane przy przechodzeniu przez materię powodują wzbudzenia atomów ośrodka, w wyniku czego następuje emisja fotonów. W większości materiałów ulegają one adsorpcji. Jednak niektóre ośrodki dielektryczne charakteryzują się przepuszczalnością pewnych długości fal. Przy przejściu naładowanej cząstki przez taki ośrodek możliwe do zaobserwowania są błyski światła. Zjawisko to zwane jest właśnie scyntylacją.

Energia cząstki możliwa jest do określenia dzięki faktowi proporcjonalności liczby emitowanych fotonów do energii straconej przez cząstkę.

Do rejestracji błysków ze scyntylatora stosuje się fotopowielacze. Na jego wyjściu otrzymywany jest impuls elektryczny. Jego wielkość jest wprost proporcjonalna do ilości fotonów.

Fotony promieniowania gamma wywołują scyntylacje pośrednie dzięki istnieniu zjawiska: fotoelektrycznego, Comptona i kreacji par pozytonowo-elektronowych.

Zjawisko fotoelektryczne:

Jest charakterystyczne dla elektronów silnie związanych w atomie, wynika z tego, że jest to oddziaływanie z całym atomem. Wynikiem tego oddziaływania jest pochłonięcie kwantu γ przez atom. Jego energia całkowita zostaje spożytkowana na wybicie elektronu.

Energia tracona w scyntylatorze równa jest energii cząstki γ.

h ν = W + E_k

gdzie:

h - stała Plancka,

ν - częstość kwantu γ,

W - energia wiązania elektronu w atomie,

E_k - energia kinetyczna wybitego elektronu.

Zjawisko Comptona:

Jest ono rozproszeniem kwantu γ na elektronie swobodnym. Efektem tego jest zmiana kierunku ruchu i energii fotonu oraz uzyskanie energii kinetycznej przez elektron.

h ν = h ν' + E_k

gdzie:

ν' - częstość fotonu rozproszonego.

Zjawisko tworzenia par elektron - pozyton:

Występuje ono przy odpowiednio wysokich energiach cząstek γ. Zajście tego zjawiska uwarunkowane jest całkowitą zamianą energii kwantu γ na energię spoczynkową i kinetyczną elektronu i pozytonu. Powstanie tego zjawiska możliwe jest jedynie w obecności trzeciej cząstki (jądra lub elektronu), uzyskującej energię i pęd odrzutu.

h ν = 2m_e + E⁺_k + E^-_k + E_k

gdzie:

m_e = 0,511 MeV - masa spoczynkowa elektronu,

E⁺_k - energia kinetyczna pozytonu,

E^-_k - energia kinetyczna elektronu,

E_k - energia odrzutu [trzeciej] cząstki.

Minimalna energia potrzebna do utworzenia pary elektron - pozyton wyrażona jest wzorem:

h ν_min = 2m_e (1 + )

gdzie:

m₀ - masa elektronu,

M - masa cząstki niezbędnej do zajścia zjawiska.

Energia progowa maleje wraz ze wzrostem masy M.

Elektron i pozyton ulegają wielokrotnemu rozproszeniu w ośrodku przekazując mu energię. W wyniku spotkania się pozytonu z elektronem ośrodka następuje ich wzajemna anihilacja. W wyniku tego wyemitowane zostają dwie cząstki γ o takich samych energiach (łączna energia 1,022 MeV - energia łączna pozytonu i elektronu).

Jeżeli obydwa kwanty, powstałych podczas anihilacji, zostaną zaabsorbowane, w scyntylatorze obserwowane jest maksimum energii całkowitej (1,022 MeV). W przypadku opuszczenia, bez oddziaływania, ośrodka przez jedną z cząstek, wyemitowanych podczas anihilacji, to pozostawiona energia równa będzie połowie energii całkowitej (0,511 MeV). Maksimum to nazywane jest maksimum pojedynczej ucieczki.

Jeżeli obie cząstki γ opuszczą ośrodek bez oddziaływania pojawia się maksimum podwójnej ucieczki.

Schematy rozpadów promieniotwórczych.

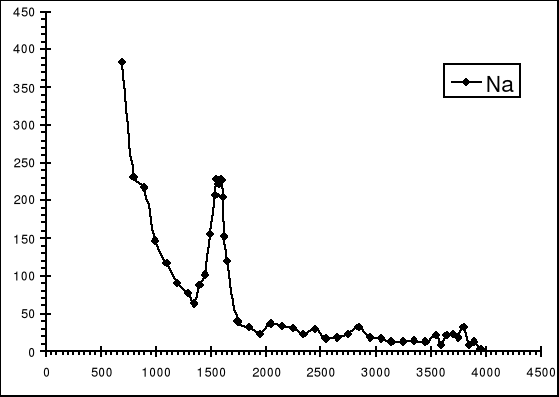
Izotop sodu rozpada się na drodze emisji β⁺ w wyniku czego powstaje jądro Na w stanie wzbudzonym, o energii wzbudzenia 1,28 MeV. Jądro to przechodzi do stanu podstawowego towarzyszy temu emisja kwantu γ. Podczas przemiany promieniotwórczej emitowany jest pozyton, który napotyka elektron i podczas anihilacji powstają dwie cząstki γ.

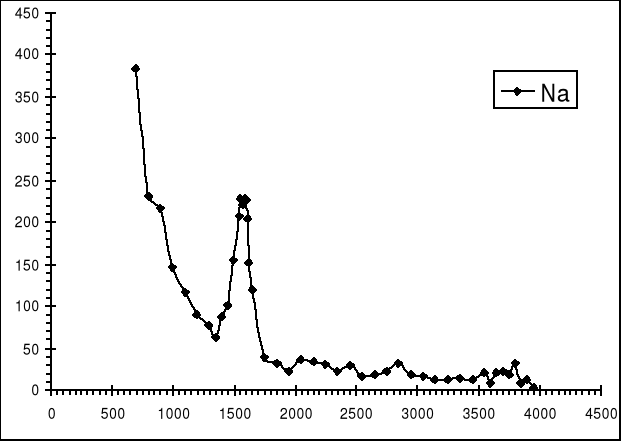
Na podstawie zarejestrowanego rozpadu promieniotwórczego uzyskano następujący wykres.

Oś X odpowiada za numer kanału, natomiast oś Y jest przedstawieniem ilości zliczeń.

Czas pomiaru wynosił 3599 sekund.

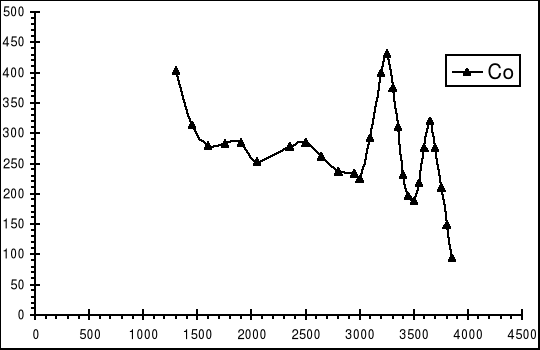
Zjawisko rozpadu Co odbywa się w wyniku emisji cząstki β^-. Efektem tej przemiany jest powstanie wzbudzonego jądra niklu (Ni) o energii 2,505 MeV lub 1,332 MeV (bardzo rzadko - 0,12%). Jądra niklu o energii 2,505 MeV przechodzą do stanu podstawowego. W wyniku tego emitowane są dwa kwanty γ, o energiach 1,173 i 1,332 MeV.

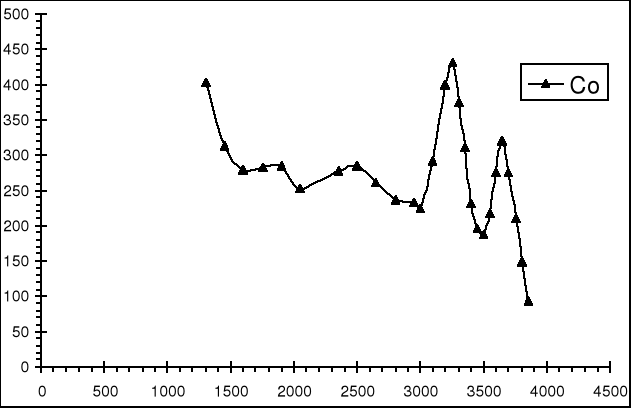
Poniżej przedstawiono wykres uzyskany na podstawie pomiarów emisji promieniowania γ pochodzącego z rozpadu Co.

Oś X odpowiada za numer kanału, natomiast oś Y jest przedstawieniem ilości zliczeń.

Czas pomiaru wynosił 290 sekund.

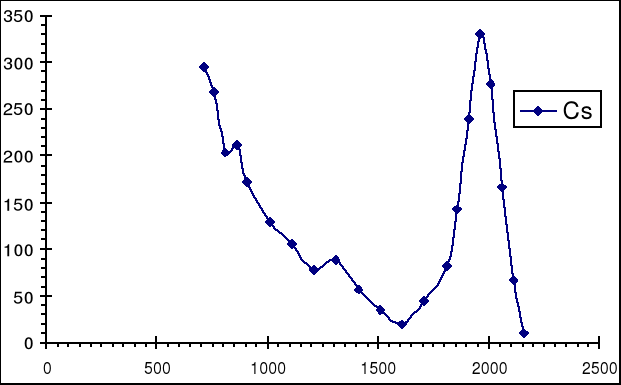
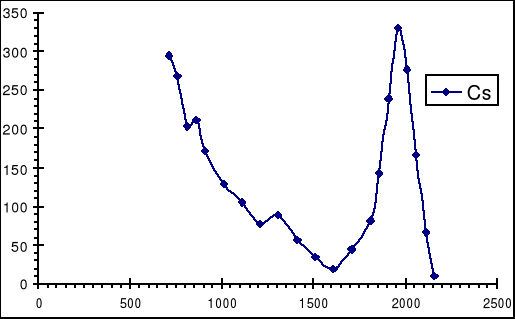
Poniżej przedstawiono widmo rozpadu izotopu ¹³⁷Cs:

Największy z pików widocznych na wykresie jest efektem zjawiska fotoelektrycznego (kanał 1960).

Czas pomiaru wynosił 120 sekund.

Obliczenia:

Poniżej zostały zestawione wartości energii i kanałów w których odnotowano maksymalne wartości zliczeń:

	kanał:	En [MeV]:
^22Na	3796
^60Co:	3250	1,173
	3650	1,332
^137Cs:	1960	0,662

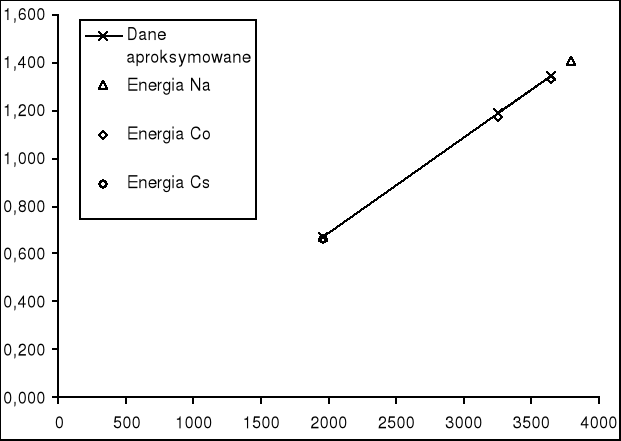
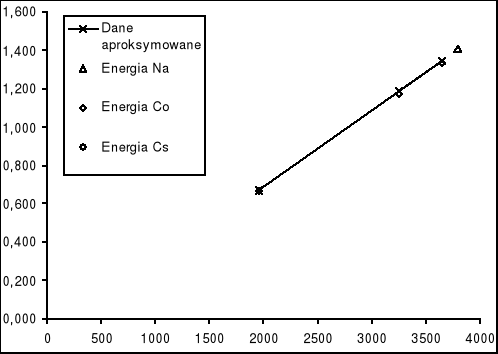
Na podstawie tych wartości została wykreślona krzywa aproksymacji.

Równanie aproksymowanej prostej:

y = 0,0004 x - 0,1149

Energię izotopu sodu wyliczono ze wzoru:

E = a k + b

Wynosi ona 1,404 MeV.

W tabeli umieszczono zestawienie energii tablicowej i wyliczonej (z prostej aproksymacji):

	Etab:	Ewyl:
Na:		1,404
Co:	1,173	1,185
	1,332	1,345
Cs:	0,662	0,669

Wnioski:

Ćwiczenie VII (#41): Wyznaczanie energii promieniowania γ za pomocą spektometru scyntylacyjnego

Wykonanie: Dziuda Beata, Król Zbigniew, Kryczka Katarzyna

- 6 -

- 7 -

- 1 -

---