W Y K Ł A D 7

WARTOŚCI ŚREDNIE I SKUTECZNE PRZEBIEGÓW OKRESOWYCH

7.1. Prąd i napięcie zmienne dla liniowych elementów R, L, C

Rezystor liniowy należy do układów bezinercyjnych

u (t) = R i (t) lub i (t) = G u (t) . (7.1)

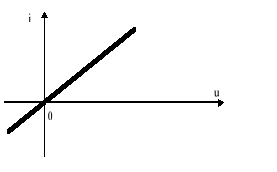
Na płaszczyźnie stanu (u, i) równanie (7.1) opisane jest linią prostą przechodzącą przez początek układu (rys.7.1).

Rys.7.1. Charakterystyka napięciowo-prądowa

liniowego rezystora dla dowolnego wymuszenia

Kondensator liniowy jest elementem inercyjnym (dynamicznym).

q (t) = C u (t) . (7.2)

. (7.3)

. (7.4)

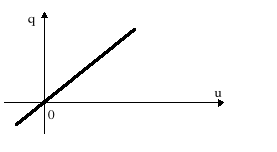
Na płaszczyźnie stanu (u,q) równanie (7.2) dla C = const. opisane jest linią prostą (rys. 7.2).

Rys.7.2. Charakterystyka liniowego kondensatora

w układzie współrzędnych (u,q)

Induktor jest elementem inercyjnym (dynamicznym) i dla L=const
(7.5)

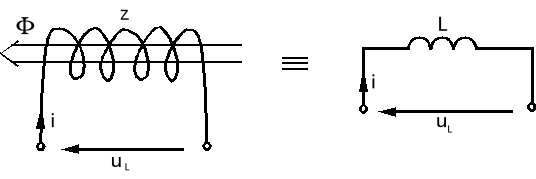
Rys.7.3. Cewka o indukcyjności L i jej symbol graficzny

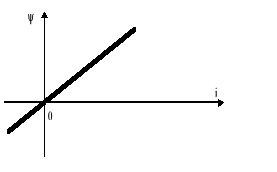
Rys.7.4. Charakterystyka liniowej cewki w układzie współrzędnych (i,ψ)

ψ = L i (7.6)

7.2. Sygnały zmienne okresowe i ich charakterystyczne wielkości

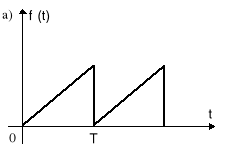
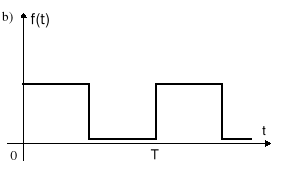
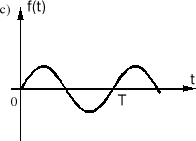
Rys.7.5. Przykładowe przebiegi okresowe: a) piłowy; b) prostokątny; c) sinusoidalny

Przebiegi przemienne:

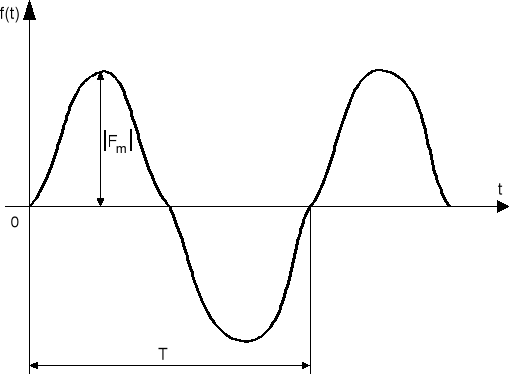
Wartość chwilowa sygnału jest to jego wartość dla dowolnej chwili czasu t.

Wartość maksymalna sygnału jest to jego największa wartość chwilowa.

Wartość średnia sygnału f(t) określona jest za pomocą następującej zależności

,
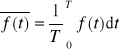
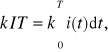
(7.9)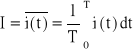
(7.10)

Wartość skuteczna sygnału okresowego f(t) o okresie T określona jest za pomocą wzoru

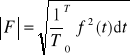
. (7.11)

Wartością skuteczną prądu okresowego i(t) (oznaczoną przez I ) nazywamy taką wartość natężenia równoważnego prądu stałego I, który na takiej samej rezystancji R wydziela w w ciągu okresu T taką samą ilość ciepła.

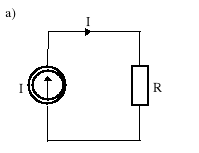
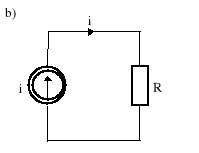
Rys.7.7. Interpretacja fizykalna wartości skutecznej prądu zmiennego: a) obwód prądu stałego; b) obwód prądu okresowego

Współczynnikiem kształtu nazywamy stosunek wartości skutecznej sygnału f(t) do wartości średniej modułu sygnału f(t) (
).

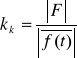
. (7.13)

Współczynnikiem szczytu nazywamy stosunek wartości maksymalnej sygnału f(t) do jego wartości skutecznej

.
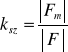
(7.14)

Przebiegi sinusoidalne:

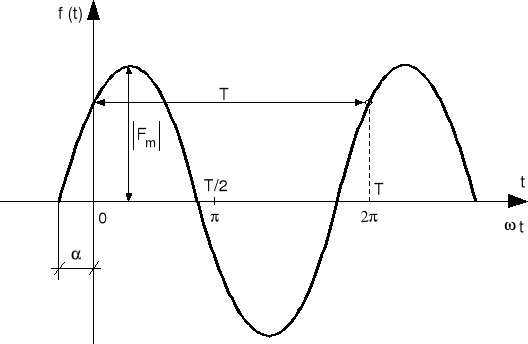
Rys.7.8. Przebieg sinusoidalny

• wartość średnia

• 
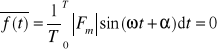
  , (7.16)

• wartość średnia modułu

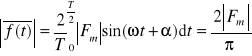
, (7.16a)

- wartość skuteczna

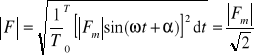
, (7.16b)
- współczynnik kształtu

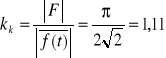
, (7.16c)
- współczynnik szczytu

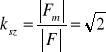
. (7.16d)

7.3. Addytywność wartości średnich prądów i napięć

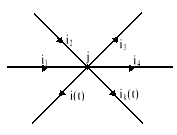
Rys.7.9. Przykładowy węzeł obwodu

, (7.17)

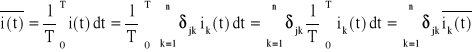
. (7.18)

II prawo Kirchhoffa jest spełnione dla wartości średnich.

1. Addytywność wartości skutecznych prądów i napięć

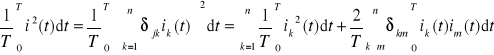
. (7.19)

Jeżeli wszystkie składniki sumy dla k≠l spełniają warunek ortogonalności, tzn., że

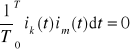
, (7.20), to
. (7.21)

, (7.21a)

1

4

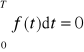
. (7.8)

Rys.7.6. Przebieg okresowy niesinusoidalny

f (t) = F_m sin (ωt + α) . (7.15)

f(t) - wartość chwilowa sygnału,

F_m- wartość maksymalna lub amplituda,

ω=2πf - pulsacja w (1rad/s),

α - faza początkowa w chwili t = 0.

---