Rachunek prawdopodobieństwa 29.10.2005

Klasyczny model r-ku pr-stwa

D - doświadczenie losowe

Ω - przestrzeń zdarzeń elementarnych - zbiór wszystkich pojedynczych wyników doświadczenia losowego

W klasycznym modelu r-ku pr-stwa zakłada się że przestrzeń zdarzeń elementarnych Ω jest zbiorem skończonym i każdy wynik doświadczenia losowego jest jednakowo prawdopodobny tj. Ω = {ω₁, ω_2……ω_n} i ∀ 1 ≤ i ≤ n, P ({ω₁}) = 1/n

W tym modelu przez zdarzenie losowe rozumiemy dowolny podzbiór Ω

A zdarzenie losowe <=> A ⊂ Ω

2^Ω rodzina wszystkich podzbiorów Ω

A∈ 2^Ω <=> A ⊂ Ω

Np.:

Ω= {1,2,3}

2^Ω={φ, {1} {2}, {1,2}, {1,3}, {2,3}, {1,2,3}}

A⊂ Ω to P(A)=

- liczba elementów zbioru A

W urnie jest M kul ponumerowanych liczbami 1,2……M losujemy n razy opisz przestrzeń zdarzeń elementarnych tego doświadczenia losowego

1) losowanie bez zwracania

n≤M

1. próbka uporządkowana

ω=(a₁, a₂,…a_n) : a_i≠a_j dla i≠j

a=1,2……M

W tym przypadku ωjest n-wyrazową wariacją bez powtórzeń zbioru M-elementowego

Ω={ω:ω=(a₁, a₂,…a_n) : a_i≠a_j dla i≠j

a=1,2……M

Ω= M (M-1)(M-2)*(M-n+1)=(M)_n

2. próbka nieuporzadkowana

ω=[a₁, a₂,…a_n] : a_i≠a_j dla i≠j

a=1,2……M

W tym przypadku ω jest to n-elementowa kombinacja bez powtórzeń zbioru M-elementowego

n-elementowy podzbiór złożony z różnych elementów ze zbioru M-elementowego

Ω={ω: ω=[a₁, a₂,…a_n] : a_i≠a_j dla i≠j}

a=1,2……M

M!=1*2*…M 0!=1

2)losowanie ze zwracaniem

a) próbka uporządkowana

ω=(a₁, a₂,…a_n) : a_i=1,2,…M

W tym przypadku ω jest n-wyrazową wariacją z powtórzeniami zbioru M-elementowego

Ω={ω:ω=(a₁, a₂,…a_n) : a_i=1,2,…M

b)próbka nieuporządkowana

ω=[a₁, a₂,…a_n] : a_i=1,2,…M i=1,2…n

W tym przypadku ω jest to n-elementowa kombinacja z powtórzeniami zbioru M-elementowego

Rzucamy tak długo moneta aż pojawi się orzeł. Przestrzeń zdarzeń tego doświadczenia jest następująca:

Ω={O, RO, RRO, RRRO,…..}

Zbiór wyników tego doświadczenia losowego jest zbiorem przeliczalnym tzn. elementy tego zbioru możemy ustawić w ciąg nieskończony

Wykres…..

Przestrzeń Ω jest zbiorem nieskończonym, który nie jest zbiorem przeliczalnym.

Ogólny model r-ku pr-stwa

D - doświadczenie losowe

Ω - przestrzeń zdarzeń elementarnych - zbiór wszystkich pojedynczych wyników doświadczenia losowego D (Ω- zbiór nieskończony, przeliczalny lub nieprzeliczalny

F - rodzina podzbioru zbioru Ω spełniającego następujące warunki

1) Ω∈F

2) jeżeli A∈F to A' = Ω\ A∈F

3)

Wtedy F nazywamy σ (sigma) podzbioru Ω

Przez zdarzenie losowe będziemy rozumieć dowolny podzbiór Ω tj. F= 2^Ω

Funkcję P: F→[0,1] spełniającą warunki:

1. P(Ω)=1 to unormowanie miary (pr-stwo zdarzenia pewnego równa się 1)

2. ∀
   

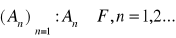
A_i ∧A_j≠φ dla i≠ j zachodzi równość:

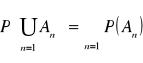
Przeliczalna addytywność nazywamy funkcję pr-stwa lub pr-stw lub miara probabilistyczną

Uporządkowaną trójkę: (Ω, F, P) nazywamy przestrzenią probabilistyczną → jest modelem matematycznym doświadczenia losowego

Pojecie zmiennej losowej

Niech (Ω, F, P) przestrzeń probabilistyczna funkcji X' : Ω spełnia warunki ∀a∈R {ω∈Ω : X(ω)<a}∈F nazywamy zmienną losową określoną na przestrzeni probabilistycznej (Ω, F, P)

(Nieprecyzyjna definicja zmiennej losowej)

Przez zmienną losową rozumiemy dowolną funkcję określona na Ω o wartościach R (X : Ω→R)

Oznaczenie F_x - dystrybuanta zmiennej losowej X

Funkcję F_x : R→[0,1]

∀x∈R F_x(x)=P {ω∈Ω  X(ω)<x}=P(X<x)

Nazywamy dystrybuantą zmiennej losowej x

Dystrybuanta jest charakterystyką funkcyjną zmiennej losowej.

Zmienne losowe skokowe (dyskretne)

Niech X zmienna losowa określona na przestrzeni probabilistycznej (Ω, F, P)

χ=x (Ω)= {x (ω):ω∈Ω}

Mówimy, że X jest zmienną losową skokowa (dyskretną) jeżeli jej zbiór wartości χ jest zbiorem skończonym lub przeliczalnym tj.

χ={x₁, x₂,…x_n} lub χ ={x₁, x₂,x₃…}

p_i=P(X=x _i) x _i∈χ

Zbiór {(x_i, P) : x_i⊂χ, p_i=P(X=x _i) nazywamy rozkładem pr-stwa zmiennej losowej X

Przykłady zmiennych losowych skokowych

1) X∼Poiss (λ),>0

P(X=k)= e ^-λ *
, k=1,2…..

Zbiorem wartości tej zmiennej jest zbiór wszystkich liczb całkowitych nieujemnych (≥0)

2)X∼Bin (n,p), n∈N, 0≤P≤1

Zmienna losowa X ma rozkład binominalny (2- mianowy) o parametrach n, p

P(X=k)=
k=0,1….n

Zmienne losowe ciągłe

Mówimy, że X jest zmienną losową ciągłą jeśli istnieje funkcja f : R→R₊ , taka, że ∀x∈R

F_x (x)=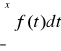

Funkcje f nazywamy funkcją gęstości pr-stwa zmiennej losowej x

Przykłady zmiennej losowej ciągłej

1. X∼Exp (α), α>0

Zmienna losowa X ma rozkład wykładniczy (eksponencjalny) z parametrem α

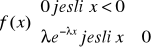
Wykres…..

2. X∼N (m,σ) m ∈R, σ >0
   

Wykres…..

Charakterystyki liczbowe zmiennych losowych

E(X) - wartość średnia lub wartość oczekiwana zmiennej X

1. X - zmienna losowa skokowa

1. χ={x₁, x₂,…x_n}

P_i=P(X=x _i), i=1,2…. (P=pr-stwo)

wtedy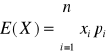

b) χ={x₁, x₂,x₃ …}

P_i=P(X=x _i), i=1,2,3….

Wtedy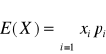
przy założeniu, że szereg stojący po prawej stronie równości definicyjnej jest zbieżny bezwzględnie tj. że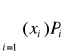
<∞

2. X zmienna losowa ciągła o funkcji gęstości pr-stwa f

Wtedy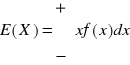
przy założeniu, że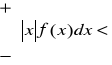

Twierdzenie o własnościach wartości średnich

Niech X₁, X₂, X₃ zmienne losowe określone na tej samej przestrzeni probabilistycznej (Ω, F, P), zakładamy, że istnieją(są skończone) E(X₁), E(X₂) , E(X) wtedy istnieje wartość średnia

1. ∃ E(X₁+X₂) i zachodzi równość E(X₁+X₂) = E(X₁) + E(X₂)

2. ∀a∈R ∃ E(aX) i zachodzi równość E(aX)=aE(X)

3. ∀c∈R E(c)=c

Wartość średnia (oczekiwana) jest najważniejszą charakterystyka zmiennej losowej

12.11.2005

Liczbę m_k: E(X^k) nazywamy k-tym momentem zmiennej losowej X

Definicja

X zmienna losowa taka, że (istnieje) ∃ E(X²) <∞

D²(X) var (x), σ²(x) wariancja zmiennej losowej X

D²(X) := E((X)-E(X))²

Stwierdzenie 1

Zakładamy, że ∃ E(X²) <∞

1. D²(X) := E(X²)-(E(X))²

2. 
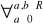
   D²(aX+b)=a²D²(X)

Dowód

a)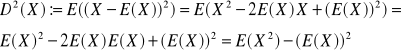

b)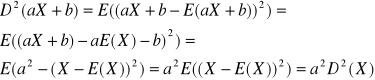

Liczbę „mi” μ : = E((X-E(X))^k) nazywamy k-tym momentem centralnym zmiennej losoej X

Wielowymiarowe zmienne losowe

Niech X₁, X₂, X₃ zmienne losowe określone na tej samej przestrzeni probabilistycznej (Ω, F, P) wtedy X:=( X₁, X₂,….. X_n) nazywamy n-wymiarową zmienna losową (lub n-wymiarowym wektorem losowym) określoną na przestrzeni probabilistycznej (Ω, F, P)

X:=( X₁, X₂,….. X_n) n-wymiarowa zmienna losowa. Załóżmy, że

∀ 1 ≤ i ≤ n ∃ E(X _i) <∞

Wtedy:

E(X)=E((X₁,X₂….X_n):=(E(X₁),E(X₂).....E(X_n))

Oprócz charakterystyk liczbowych pojedynczych zmiennych losowych zdefiniowano charakterystyki liczbowe pary zmiennych losowych mówiącą o ich powiązaniach. Zależność pomiędzy zmiennymi losowymi mierzymy za pomocą kowariancji
i współczynnika korelacji.

Definicja

X i Y zmienne losowe takie, że

∃ E(X²), E(Y²) <∞

Cov (X,Y) : = E((X-E(X))(Y-E(Y)))

Odchylenie standardowe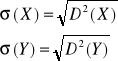

Definicja

Przy założeniach definicji poprzedniej

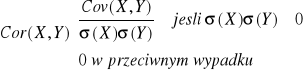
współczynnik korelacji

Współczynnik korelacji jest to kowariancja odniesiona do iloczynu odchyleń standardowych - unormowana kowariancja.

Definicja

X₁, X₂,….X_n zmienne losowe określone na tej samej przestrzeni probabilistycznej (Ω, F, P). Mówimy, że zmienne losowe X₁, X₂, ….X_n są niezależne jeśli:

∀ x₁,x₂,….x_n ∈ R zachodzi równość

P(X₁<x₁, X₂<x₂….. X_n<x_n)= P(X₁<x₁)….P(X_n<x_n)

Pojęcie niezależności jest fundamentalnym pojęciem probabilistyki. Pojęcie to wyodrębnia teorię pr-stwa z teorii funkcji rzeczywistej (z analizy matematycznej).

Twierdzenie

X₁, X₂,….X_n zmienne losowe E(X₁,X₂….X_n)=E(X₁)….E(X_n)

Wniosek

Jeżeli X₁, X₂,…X_n zmienne losowe, to wtedy D²(X₁,X₂…X_n)= D²(X₁)+ D²(X₂)+…+ D²(X_n)

Pojęcie macierzy kowariancyjnej

Definicja

X=(X₁,X₂….X_n) n-wymiarowa zmienna losowa, zakładamy, że

∀ 1 ≤ i ≤ n ∃ E(X _i²) ⊂ ∞

Macierz [Cov(X_i, Y_j)]ⁿ, i,,j=1 nazywamy macierzą kowariancyjną n-wymiarowej zmiennej losowej X=(X₁…..X_n)

Stwierdzenie

X, Y zmienne losowe takie, ze ∃ E(X²), E(Y²) <∞

a) Cov (X, Y)= E(X-Y)-E(X)E(Y)

b) jusli X, Y nielalezne zmienne losowe to cor (X,Y)=0 (Cov(X,Y)=0)

Dowód

1. Cov (X.Y) =E((X-E(X))(Y-E(Y)))=E(XY-XE(Y)-E(X)Y+E(X)E(Y)=

E(X*Y)-E(X)E(Y)-E(X)E(Y)+E(X)E(Y)=

E(XY)-E(X)E(Y)

2. X,Y zmienne niezależne => E(XY)=E(X)E(Y) =>Cov (X,Y) = E(X-Y)-E(X)E(Y)=0

=>cor(X,Y)=0

UWAGA!

Stwierdzenie odwrotne do punktu b) nie zachodzi tzn. jeśli cor(X,Y)=0 to nie wynika z tego, ze zmienne x,Y są niezależne

X - cecha mieszana populacji generalnej

x - zmienna losowa

Fx(x,θ) - dystrybuanta θ - parametr rozkładu

Fx(x,θ)=P(X<x) ∀a∈R

(X₁,X₂….X_n) n-wymiarowa zmienna losowa, zakładamy, że

∀ 1 ≤ i ≤ n X_i∼X ( zmienna losowa X_i ma taki sam rozklad jak zmienna losowa X) oraz że zmienne losowe X₁,X₂….X_n nazywamy n - elementową próba losową (prostą)

Estymacja (szacowanie) punktowe. Estymatory i ich podstawowe właściwości.

W przypadku gdy rozkład badanej populacji cechy mierzalnej nie jest znany zachodzi często potrzeba oszacowania pewnych parametrów tego rozkładu. Niech rozkład badanej cech X populacji zależy od nieznanego parametru θ („teta”). Parametr ten będziemy szacować (estymować) na podstawie n- elementowej próby prostej (X₁,X₂….X_n) pobranej z tej populacji g(X₁,X₂….X_n) będące funkcja próby losowej (X₁,X₂….X_n) nazywamy statystykami. Rozkład pr-stwa takiej zmiennej zależy od postaci funkcji g oraz od rozkładu zmiennej X₁,X₂….X_n

Każdą statystykę
, której wartości przyjmujemy jako oceny nieznanego parametru θ nazywamy estymatorem parametru θ. Otrzymana na podstawie jednej konkretnej realizacji próby wartość estymatora nazywamy oceną (oszacowaniem) tego parametru.

Własności estymatorów

Mówimy, ze estymator
parametru θ jest zgodny, jeśli
∀ε>0

Własność zgodności oznacza, ze dla dostatecznie dużych liczności próby estymatora przyjmuje z dużym pr-stwem wartości bliskie estymowanemu parametrowi θ.

Estymatorem zgodnym nieznanej wartości oczekiwanej θ = E(X) < ∞ dowolnego rozkładu jest statystyka

Estymator
nazywamy estymatorem nieobciążonym parametrem θ jeśli ∀ n∈N E
=θ _n

jeśli istnieje E
i E
to mówimy, ze estymator
jest estymatorem obciążonym parametrem

Liczbę B_n(θ):E(
) - θ nazywamy obciążeniem estymatora

Jeśli
to mówimy, że estymator
jest estymatorem asymptotycznie nieobciążonym parametru θ.

Metody otrzymywanie estymatorów

1. Metoda momentów

2. Jeśli mamy próbę losowa (X₁,X₂….X_n) to możemy określić tzw. momenty z próby w sposób analogiczny do definicji momentów zmiennej losowej

m_k=E(X^k) k=1,2….

A_k
nazywamy k-tym momentem próby losowej

A_k

Podobnie określamy momenty centralne „mi” μ_k = E((X-E(X))^k)

k-ty moment centralny zmiennej losowej X
zazywamy k-tym momentem centralnym próby losowej (X₁,X₂….X_n)

μ_k = E((X-E(X))²)=D²(X)

drugi moment centralny próby losowej (X₁,X₂….X_n)

S_n²=B₂

S_n² jest estymatorem (obciążonym) wariancji cech populacji (rozkładu)

Metoda momentów jest najstarszą metodą szacowania parametrów. Polega ona na tym, że do szacowania parametrów populacji generalnej używamy odpowiednich momentów z próby lub ich funkcji

Jeśli chcemy oszacować wartość średnią to ponieważ jest to pierwszy moment jako estymatora używamy I momentu z próby. Chcąc oszacować wariancję, która jest II momentem centralnym jako estymatora używamy II momentu centralnego z próby

Metoda momentów charakteryzuje się dużą prostota ale estymatory uzyskane przy pomocy tej metody nie mają na ogół dobrych własności. Są z reguły estymatorami obciążonymi poza estymatorem

jest estymatorem obciążonym wariancją σ² (σ²=D²(X))

jest estymatorem nieobciążonym wariancji wariancją σ² (σ²=D²(X))

Estymatory S_n² i S_n^*2 sa estymatorami nieznanych wariancji σ² (σ²=D²(X))

Estymacja przedziałowa 26.11.2005

Estymacja przedziałowa parametru θ polega na znalezieniu 2 statystyk θ₁=θ₁(X₁,X₂….X_n) i θ₂=θ₂(X₁,X₂….X_n) spełniających warunki:

P(θ₁(X₁,….X_n)< θ < θ₂(X₁, ….X_n)=1-α, gdzie 1-α jest liczbą bliską jedności

Szukamy przedziału (θ_1, θ₂), którego końcami są zmienne losowe, a który zawiera nieznany parametr θ z pr-stwem równym 1-α.

Przedział (θ_1, θ₂) nazywamy przedziałem ufności a pr-stwo 1-α poziomem ufności (lub współczynnikiem ufności)

Z definicji przedziału ufności końce tego przedziału są zmiennymi losowymi. Nieznana wartość parametru θ może być więc pokryta przez ten losowy przedział albo też nie. Jeżeli jednak dla różnych zaobserwowanych próbek losowych (x₁,x₂….x_n) znajdziemy wiele realizacji przedziału ufności to częstość tych które będą zawierać rzeczywistą wartość parametru θ w dużej liczbie tych realizacji będzie w przybliżeniu równa 1-α

MODEL I

Przedział ufności dla średniej normalnej gdy wariancja jest znana

Niech cecha X elementów populacji generalnej ma rozkład N(m, σ) tzn., że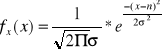
, ∀x∈R

E(X)=m, D²(X)= σ², m∈R, σ>0, m-nieznane, σ-znane

Niech (X₁, X₂….X_n) prosta próba losowa pobrana z populacji normalnej o rozkładzie normalnym N(m, σ) tzn.,

∀ 1 ≤ i ≤ n X_i∼X oraz zmienne losowe X₁, X₂….X_n są (stochastycznie) niezależne.

Z r-ku pr-stwa wiadomo, że statystyka
ma rozkład normalny (
)

∼ N(
)

Stąd wynika, że zmienna standaryzowana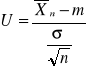
∼ N (0,1)

W tablicach rozkładu normalnego można znaleźć u_α spełniającą warunek P(-u_α<U< u_α)=1-α

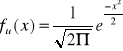
∀x∈R

Wykres

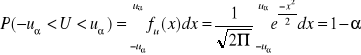
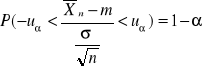
Rozwiązujemy powyższą nierówność względem m

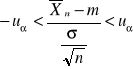
Powyższe 3 nierówności są równoznaczne

Stąd mamy:

P(
)=1-α

Z powyższej równości otrzymujemy wzór na przedział ufności dla średniej normalnej n gdy σ² jest znane na poziomie ufności 1-α

przedział ufności

Długość tego przedziału jest równa

Długość przedziału ufności dla średniej normalnej jest proporcjonalna do odchylenia standardowego σ a odwrotnie proporcjonalna do

α	0,1	0,005	0,0495	0,01	0,001
u	1,645	1,96	2	2,576	3,291
1-α	90%	95%	95,05%	99%	99,9%

Na poziomie ufności 1-α=95% przedział ufności dla średniej normalnej m, gody σ² jest znane wyraża się wzorem

Otrzymany w tym modelu przedział ufności dla średniej normalnej stosuje się w przypadku próby dużej o liczebności n ≥30 wtedy wariancję σ² można ocenić na podstawie wartości nieobciążonego estymatora wariancji

Przykład 1

Z pewnej populacji dorosłych mężczyzn wylosowano n=100 zmierzono ich wzrost. Otrzymano następujące sumy

Znajdź realizacje przedziałów ufności dla średniej normalnej na poziomie ufności 95% i 99%

Zał: wzrost ma rozkład normalny

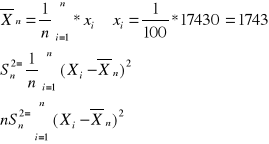
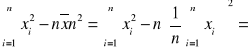
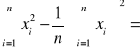
3057149-1/100*(17430)²=19100

Ponieważ próba jest liczna to:

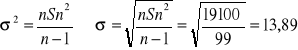
1-α=95% u_α=1,96

(174,3-1,96*
, 174,3+1,96*
)

(170,72 , 177,88)

Model II

Przedział ufności dla średniej normalnej gdy wariancja jest nieznana

Zakładamy, że cecha X ma rozkład N(m, σ), gdzie m, σ nieznane

(X₁,X₂….X_n) prosta próba losowa pobrana z tej populacji. Można pokazać ze statystyki
i nSn² są stochastycznie niezależne oraz
∼ χ²(n-1)

Definicja X₁,X₂….X_n niezależne zmienne losowe takie, że

∀ 1 ≤ i ≤ n X_i∼N (0, 1) wtedy mówimy, że zmienne losowe χ²(n)=X₁²+X₂²….+X_n² ma rozkład chi kwadrat z n stopniami swobody

Rozkład χ² został wprowadzony przez Karla Pearsona. Rozkład χ² jest rozkładem stablicowanym.

Tworzymy 2 nowe zmienne losowe:

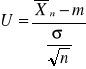
∼N (0, λ)

∼χ²(n-1)

Definicja (Rozkład t-Studenta)

Niech U∼N (0,1), V∼χ²(k), zakładamy, że zmienne U i V są niezależne. Wtedy mówimy, że zmienna losowa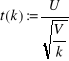
ma rozkład t-Studenta z k stopniami swobody

Rozkład ten został wprowadzony przez W. Gosset (1976-1937) używającego pseudonimu Student.

Zgodnie z powyższa definicją zmienna losowa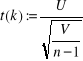
∼t(n-1)

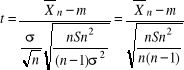
∼t(n-1)

W tablicach rozkładu t-Studenta można znaleźć wartość t_α=t_{(α, n-1)} spełniające warunek

P(-t_α<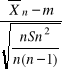
< t_α )= 1-α

Poniższa nierówność

-t_α<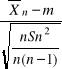
< t_α

jest równa następującej podwójnej nierówności

-t_α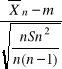
<
< t_α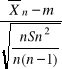

A to jest równoważne:

-t_α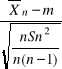
<m<
+t_α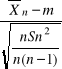

Stąd otrzymujemy

P(
-t_α
<m<
+t_α
)=1-α

Z powyższego wzoru mamy, że przedział (
-t_α
<m<
+t_α
) jest przedziałem ufności dla średniej normalnej m gdy σjest nieznane na poziomie ufności 1- α

Przedział ten ma zastosowanie gdy dysponujemy próbą małej liczności n≤30

Przedział ufności dla wariancji i odchylenia standardowego 10.12.2005

Model I

Cecha X elementów populacji generalnej ma rozkład N (m, σ), gdzie m, σ są nieznane

Próba jest liczności n≤50

Konstrukcję przedziałów oprzemy na statystyce

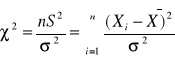
Która ma rozkład chi - kwadrat z (n-1) stopniami swobody. Rozkład ten oznaczamy przez χ² (n-1). Wtedy:

Liczby χ² (½α, n-1) i χ² (1-½α, n-1) nazywamy kwadratami rzędu ½α i 1-½α rozkładu χ² z n-1, ½α,

Wykres 1

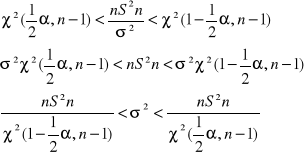
Stąd mamy ze prawdopodobieństwo

P(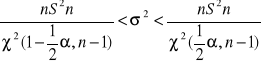
)=1-α

Otrzymaliśmy wzór na przedział ufności dla wariancji σ² na poziomie ufności 1- α

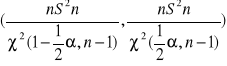
Stąd mamy ze pr-stwo

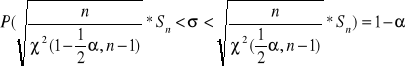
Otrzymaliśmy wzór na przedział ufności dla odchylenia standardowego σ² na poziomie ufności 1-α

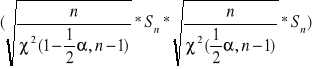
Model II

Cecha X elementu populacji generalnej ma rozkład N (m, σ), gdzie m, σ są nieznane

Próba jest liczności n≥50

W przypadku tego modelu można wykorzystać fakt, że statystyka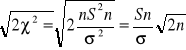

Ma w przybliżeniu rozkład N(
1) zatem

Gdzie
jest kwantylem rzędu
rozkładu N(0, 1)

Rozwiązujemy następujące podwójne nierówności ze względu na σ

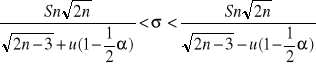
Stąd mamy wzór na przedział ufności dla σ na poziomie ufności 1-α

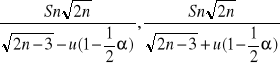
Elementy rachunku prawdopodobieństwa

Rozkład Snedecora

Rozkładem Snedecora ze stopniami swobody (r₁,r₂) nazywamy rozkład pr-stwa iloraz

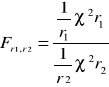
Gdzie
,
SA niezależnymi zmiennymi losowymi o rozkładzie
stopniami swobody odpowiednio

E

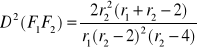
Wykres 2

Rozkład ten jest rozkładem stablicowanym

Dla danych prawdopodobieństw α i ustalonych liczb stopni swobody α(r₁, r₂) dana jest wartość

Twierdzenia o rozkładzie sumy nierealnych zmiennych losowych

Twierdzenie 1

Niech X₁, X_2……X_n niezależne zmienne losowe takie, że ∀ 1≤ i≤ n X_i ~N(m,σ)

Wtedy zmienne losowe
X_i ~N(m₁+ m_2+….+ m_n ,
)

Z twierdzenia 1 wynika:

Jeśli X₁, X_2……X_n niezależne zmienne losowe takie, że ∀ 1≤ i < n X_i ~N(m,σ) wtedy

X_i ~N(nm,
)

Twierdzenie 2

X₁, X₂ niezależne zmienne losowe takie, że X_i ~N(m_i,σ_i), i=1,2

Wtedy zmienna losowa Z=X₁-X₂ ~ N(m₁-m_2,
)

Stąd wynika, że jeśli X₁, X₂ niezależne zmienne losowe takie, że X_i ~N(m,σ), i=1,2 Wtedy zmienna losowa Z=X₁-X₂ ~ N(0,
)

Twierdzenie 3

X₁, X_2……X_n niezależne zmienne losowe takie, że ∀ 1 i ≤ n X_i ~N(m,σ)

Wtedy
X_i ~N(
(m_{1 +….+} m_n) ,
)

Weryfikacja hipotez statystycznych

Obok zagadnień estymacji 2 podstawowym działem wnioskowania statystycznego jest weryfikacja hipotez statystycznych

Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawidłowości lub fałszywości którego wnioskuje się w oparciu o pobraną próbkę. Hipotezy które dotyczą wyłącznie wartości parametru (parametrów) określanej klasy rozkładów nazywamy hipotezami parametrycznymi

Np.:

Cecha X ~N(0,σ)

Wysuwamy hipotezę σ =1

Każdą hipotezę, która nie jest parametryczna nazywamy nieparametryczną.

Np.:

Niech T oznacza czas między 2 kolejnymi zgłoszeniami do centrali telefonicznej. Wysuwamy hipotezę, że T ma rozkład wykładniczy.

Jeżeli hipoteza parametryczna precyzuje dokładnie wartość wszystkich parametrów rozkładu badanej cechy to nazywamy ją hipotezą prostą, w przeciwnym wypadku mówimy o hipotezie złożonej. Weryfikację postawionych hipotez statystycznych przeprowadzamy w oparciu o próby losowe.

Metodą postępowania, która każdej realizacji próbki (x₁, x₂….x_n) przyporządkowuje z ustalonym pr-stwem decyzję przyjęcia lub odrzucenia sprawdzonej hipotezy nazywamy testem statystycznym. W praktyce przy weryfikacji hipotez postępuje się w ten sposób że oprócz weryfikowanej hipotezy H₀ wyróżnia się inną hipotezę H₁, która najczęściej wynika z celu badania statystycznego (zwana jest hipotezą alternatywną)

H₁ jest taką hipotezą, którą w danym zagadnieniu skłonni jesteśmy przyjąć jeśli weryfikowaną hipotezę H₀ należy odrzucić

W celu zbudowania testu do weryfikacji postawionej H₀ należy wybrać odpowiednią funkcję próby losowej „delta” δ(X₁, X₂…..X_n) nazywamy statystyką testową.

Przy pobieraniu różnych próbek nawet tej samej liczności funkcja ta przyjmuje na ogół różne wartości. Jedne z nich będą świadczyły o zgodności weryfikacji z hipotezą a inne będą przemawiać przeciw tej hipotezie. Zachodzi więc konieczność podziału zbioru wszystkich wartości, które może przyjąć statystyka testowa.

δ(X₁, X₂…..X_n) ma 2 dopełniające się zbiory W i W', takie, że jeśli δ(X₁, X₂…..X_n) є W to hipotezę odrzucamy

Jeżeli δ(X₁, X₂…..X_n) є W' to hipotezę przyjmujemy. Zbiór W nazywamy zbiorem krytycznym lub zbiorem odrzuceń hipotezy. Zbiór W' nazywamy zbiorem przyjęć.

Weryfikując daną hipotezę statystyczną H₀ w oparciu o zaobserwowane wyniki próbki ponosimy zawsze pewne ryzyko podjęcia błędnej decyzji. Wynika to stąd że na podstawie próbki nigdy nie mamy całkowitej informacji o zbiorowości z której została pobrana próbka. W wyniku testowania hipotezy statystycznej możemy podjąć poprawna decyzję albo popełnić 1 z 2 następujących błędów:

1. możemy odrzucić weryfikowana hipotezę H₀ wtedy gdy jest ona w rzeczywistości prawidłowa - błąd I rodzaju

2. możemy przyjąć weryfikowaną H₀ jako prawdziwą podczas gdy jest ona fałszywa czyli jeśli prawdziwa jest hipoteza alternatywna H₁- błąd II rodzaju

Pr-stwo błędu I rodzaju nazywamy poziomem istotności i oznaczamy α . Pr-stwo błędu II rodzaju oznaczamy β

Pożądane jest aby pr-stwo błędów obu rodzajów uczynić możliwie małym. Nie można jednak zmniejszać jednocześnie obydwu rodzajów błędów przy ustalonej liczności próby

Weryfikacja hipotez dotycząca wartości średniej 7.01.2006

MODEL I

Badana cecha X populacji generalnej ma rozkład N(m, σ), gdzie σ >0 jest znane.

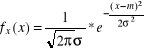
E(X)=m, D²(X)= σ²

Weryfikujemy hipotezę H₀:m=m₀ wobec hipotezy alternatywnej

1. H₁:m=m_{1 <} m₀

2. H₁:m=m_{1 >} m₀

3. H₁:m=m_{1 ≠} m₀

Poziom istotności α, 0<α<1

Do weryfikacji hipotezy H₀ użyjemy statystyki
, która przy prawdziwości hipotezy H₀:m=m_{0 ma} rozkład N(0,1)

Jeśli H₁:m=m_{1 <} m₀ to zbiorem krytycznym W jest przedział [(1-α), +∞), gdzie u(1-α) jest kwantylem rzędu 1-α rozkładu N(0,1)

konstrukcja testu do weryfikacji hipotezy H₀:m=m₀ wobec hipotezy alternatywnej H₁:m=m_{1 <} m₀ na poziomie istotności α

Wykres...

Jeśli H₁:m=m_{1 ≠} m₀ to zbiorem krytycznym W jest suma przedziałów (-∞, u(1-α/2)] ∪[(1-α/2) +∞)

Wykres....

Jeśli wartość statystyki U jest obliczana dla próbki u_obl należy do zbioru krytycznego W to weryfikowaną hipotezę H₀ odrzucamy a przyjmujemy hipotezę alternatywną H₁. W przeciwnym przypadku nie ma podstaw do odrzucenia weryfikowanej hipotezy H₀.

Przyklad

Z populacji w której badana cecha X ma rozkład normalny X ~N(m,4) wylosowano próbkę o liczności n=9. Na poziomie istotności α=0,05 zweryfikować hipotezę H₀: m=2 wobec hipotezy H₁m=m₁ < 2 jesli średnia z próbki wynosi
=1,4

H₁m=m₁ < m₀=2 to zbiór krytyczny W=(-∞, u(1-α)]=(-∞, u(0,95)]= (-∞,-1,64]

MODEL II

Badana cecha X populacji generalnej ma rozkład N(m, σ), gdzie m, σ nieznane.

Weryfikujemy hipotezę H₀:m=m₀ wobec hipotezy alternatywnej

a) H₁:m=m_{1 ≠} m₀

b) H₁:m=m_{1 >} m₀

c)H₁:m=m_{1 <} m₀

Poziom istotności α, 0<α<1

Do weryfikacji hipotezy H₀ użyjemy statystyki
, która przy prawdziwości hipotezy H₀:m=m₀ ma rozkład t-Studenta z n-1 stopniami swobody.

Jeśli m_{1 >} m₀ to zbiorem krytycznym jest przedział [t(1- α, n-1), +∞), gdzie t(1- α, n-1) jest kwantylem rzędu 1-α rozkładu t-Studenta z n-1 stopniami swobody

Jeśli m_{1 <} m₀ to zbiorem krytycznym jest przedział (-∞, - t(1- α, n-1)]

Jeśli m_{1 ≠} m₀ to zbiorem krytycznym jest przedział (-∞, - t(1- α/2, n-1)]∪[ t(1- α/2, n-1), +∞), gdzie t(1- α/2, n-1) jest kwantylem rzędu 1- α/2 rozkładu t- Studenta z n-1 stopniami swobody.

Jeśli wartość t_obl statystyki t obliczona dla danej próbki należy do zbioru krytycznego W wtedy weryfikowaną hipotezę H₀ odrzucamy na korzyść hipotezy alternatywnej H₁. W przeciwnym przypadku nie ma podstaw do odrzucenia weryfikowanej hipotezy H₀.

Testy istotności dla wariancji

Niech badana cecha X populacji generalnej ma rozkład N(m, σ), gdzie m, σ nieznane.

Weryfikujemy hipotezę H₀:σ ² =σ²₀ wobec hipotezy alternatywnej

a) H₁: σ ² =σ²₁ ≠σ ²₀

b) H₁: σ ² =σ²_{1 >} σ ²₀

c)H₁: σ ² =σ²_{1 <} σ ²₀

Poziom istotności α, 0<α<1, n≤50

Do weryfikacji hipotezy H₀ użyjemy statystyki
, która przy prawdziwości hipotezy H₀ ma rozkład χ² (n-1). Jeśli H₁: σ ² =σ²_{1 >} σ ²₀ wtedy zbiorem krytycznym W jest przedział [χ²(1-α, n-1), +∞) gdzie χ²(1-α, n-1) jest kwantylem rzędu 1-α z n-1 stopniami swobody

Wykres...

Jeśli H₁: σ ² =σ²_{1 <} σ ²₀ to W (0, χ²(α, n-1)

Wykres...

Jeśli H₁: σ ² =σ²₁ ≠σ ²₀ to W (0, (1/2α, n-1)] ∪ [(1-1/2α, n-1), +∞)

Jesli obliczona z próbki wartość statystyki
należy do zbioru krytycznego W to weryfikowaną hipotezę H₀ odrzucamy i przyjmujemy hipotezę alternatywną. W przeciwnym przypadku nie ma podstaw do jej odrzucenia.

UWAGA

Ponieważ tablice rozkładu χ² podają wartości kwantyli dla n≤50 to rozpatrzony model stosujemy przy założeniu, że próbka jest o liczności n≤50

Przykład

W celu oszacowania dokładności pomiaru wykonanych pewnym przyrządem dokonano n=8 pomiarów i otrzymano następujące wyniki: 18,17; 19,21; 18,05; 18,14; 18,19; 18,22; 18,06; 18,08;

α=0,05 H₀; σ ² =σ²₀ przeciw hipotezie alternatywnej:

a) H₁: σ ² =σ²₁ ≠σ ²₀

b) H₁: σ ² =σ²_{1 >} σ ²₀

c)H₁: σ ² =σ²_{1 <} σ ²₀

Poziom istotności α, 0<α<1, n>50

Do weryfikacji hipotezy H₀ wykorzystamy jak w poprzednim modelu statystykę
oraz fakt, że statystyka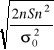
ma w przybliżeniu rozkład N(
, 1)

Do weryfikacji H₀ użyjemy statystyki
, która ma w przybliżeniu rozkład N(0,1)

1) jeśli H₁: σ ² =σ²_{1 >} σ ²₀ to zbiorem krytycznym W jest przedział [u(1-α), +∞), gdzie u(1-α) jest kwantylem rzędu 1-α rozkładu N(0,1)

2) jeśli H₁: σ ² =σ²_{1 <} σ ²₀ to zbiorem krytycznym W jest przedział (-∞, - u(1-α)]

3) jeśli H₁: σ ² =σ²₁ ≠σ ²₀ to zbiorem krytycznym W jest przedział ((-∞, - u(1-α/2)]∪[ u(1-α/2), +∞)

---