Zginanie prętów silnie zakrzywionych

Przez pręty silnie zakrzywione rozumie się takie, dla których nie można przyjąć, że proporcja pomiędzy poprzecznym wymiarem przekroju pręta  h a promieniem krzywizny  R jest pomijalnie mała. W praktyce jako graniczną wartość można przyjąć hR /, = 0 2. Prętami silnie zakrzywionymi mogą być np. haki, ogniwa łańcuchów, wyoblone naroża ram itd.

Badania doświadczalne oraz rozważania teorii sprężystości wykazały, że także dla prętów silnie zakrzywionych słuszna jest hipoteza płaskich przekrojów Bernoulliego. W związku z tym rozkład przemieszczeń obwodowych u na wysokości przekroju można przyjąć jako liniowy.

Winkler Emil

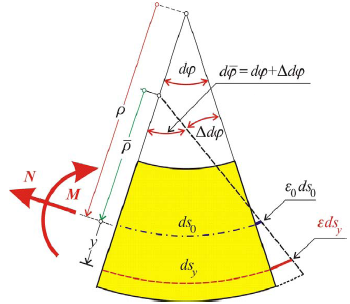
Początkowa długość włókien:

Deformacja wywołana obciążeniem powoduje:

Przekrój obraca się względem punktu nie leżącego na osi x.

Długość włókien w wyniku deformacji:

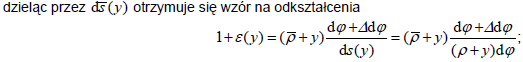
Rozważając jeszcze raz długość włókien w deformacji wynika, że;

Z prawa Hooke'a mamy :

Niewiadome odkształcenia
i
wyznacza się bezpośrednio z definicji przekrojowych sił wewnętrznych.

Ponieważ , oznaczając i przekształcając:

Co po podstawieniu do wzoru na naprężenia daje:

Wzór ten wskazuje, że:

1. Przebieg naprężeń jest krzywą hiperboliczną.

2. Dla N=0 (czyste zginanie) oś zerowa nie przechodzi przez środek ciężkości.

3. Dla
   wzór przyjmuje klasyczną postać jak dla belki zginanej.

---