MATEMATYKA FINANSOWA
Rachunek odsetek prostych
Wykorzystywany w okresie krótkim do 1 roku
Wzór ogólny
![]()
Wzór przy uwzględnieniu odniesienia czasowego
![]()
np. w przypadku okresu dziennego
![]()
Zadanie 1
Od jakiej kwoty otrzymano 15 zł odsetek za okres 2 miesięcy przy stopie procentowej 18% w skali roku.
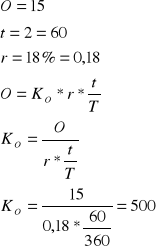
Zadanie 2
Przy jakiej stopie procentowej przypada 4 zł odsetek od kwoty 200 zł za 30 dni
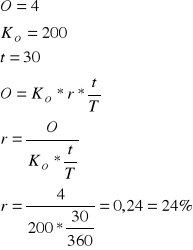
Wzór na kapitał końcowy
![]()
Wzór na kapitał końcowy, gdy odnosimy się do okresów rocznych
![]()
Zadanie 3
Wpłacono do banku kwotę 850 zł wkład ten jest oprocentowany wg stopy procentowej 14% w skali roku. Jaki będzie stan konta w dwóch latach?
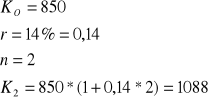
Zadanie 4
Po ilu latach kapitał początkowy w wysokości 750 zł złożony na 11% podwoi się
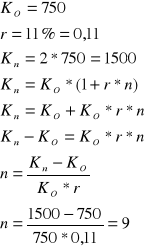
Wzór na odsetki przy regularnych kwotach wpłat
![]()
gdzie :
K - kwota wpłaty
r - stopa procentowa
n - ilość wpłat
m - częstotliwość wpłat
Wzór na kapitał końcowy
![]()
Zadanie 5
Jaką wielkość należy wpłacać przez 3 kwartały, aby zgromadzić wraz z odsetkami kwotę 1500 zł, roczna stopa procentowa wnosi 10%
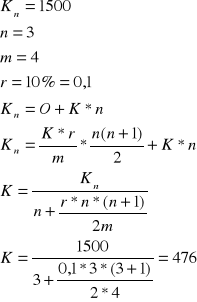
Zadanie 6
Wyznaczyć wartość lokaty 10000 zł po upływie roku, jeżeli w pierwszych 5 miesiącach stopa procentowa wynosiła 12% a w kolejnych siedmiu 10%
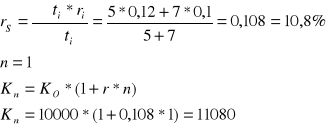
Zadanie 7
Kupujesz urządzenie za 10000 zł zapłatę odroczono o 45 dni przy stopie procentowej, 27% jaką kwotę zapłacisz regulując zobowiązanie
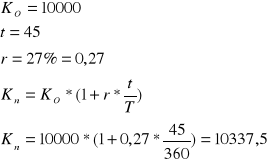
Zadanie 8
Ulokowałeś 100 zł na 6 lat, stopa oprocentowania zmieniała się, co 2 lata i wynosiła odpowiednio 17%, 15%, 13% jaką kwotę dysponujesz powyżej wymienionym okresie utrzymywania lokaty
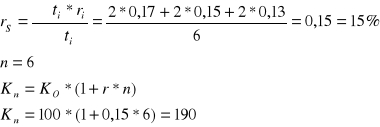
Zadanie 9
Przez ile kwartałów powinno się wpłacać kwotę po 50 zł aby stan konta przy oprocentowaniu 35% w skali roku wyniósł 941,25 zł
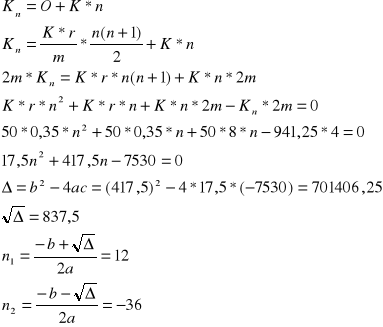
Zadanie 10
Ulokowano w banku kwotę 600 zł w dniu 5 marca nominalna stopa procentowa 36%, jaką kwotę pobierze lokato dawca w dniu 9 maja tego samego maja, jeśli odsetki nie są kapitalizowane
dzień |
miesiąc |
9 |
5 |
5 |
3 |
4 |
2 |
2 miesiące i 4 dni = 2*30+4 = 64 dni
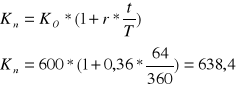
Zadanie 11
Ile powinno się trzymać kapitał, aby wzrósł on, co najmniej 2,5 raz, ale nie więcej niż 3 razy przy rocznej stopie procentowej 14%
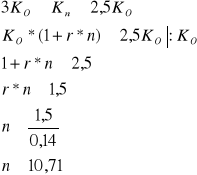
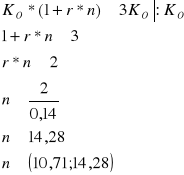
Zadanie 12
Pod koniec każdego z 5 kolejnych miesięcy wpłacamy na rachunek bankowy 500 zł przy oprocentowaniu, 10% jaką kwotę będziemy dysponować na koniec 5 miesiąca.
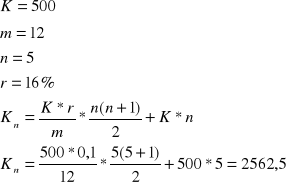
Rachunek oprocentowania składanego
Zadanie 1
Ulokowałeś 100 zł na 6 lat, stopa oprocentowania zmniejszała się, co 2 lata i wynosiła odpowiednio 17,15,13. Jaką kwotą dysponujesz po wyżej wymienionym okresie lokaty w przypadku?
kapitalizacji rocznej
oprocentowania ciągłego
a)
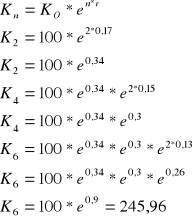
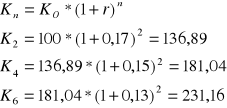
b)
Zadanie 2
Chcesz ulokować 1000 zł na 2 lata, cztery banki oferują poniższe warunki dla lokat
Bank A - oprocentowanie proste, r = 20%, kapitalizacja na koniec okresu
Bank B - oprocentowanie nominalne 19%, kapitalizacja kwartalna
Bank C - oprocentowanie efektywne 20,5%
Bank D - oprocentowanie nominalne 18,5%, kapitalizacja ciągła
Który z banków oferuje najlepsze warunki. Dla każdego z banków znaleźć oprocentowanie efektywne.
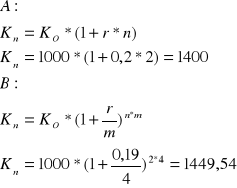
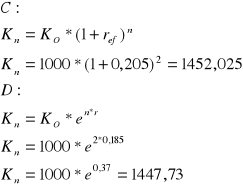
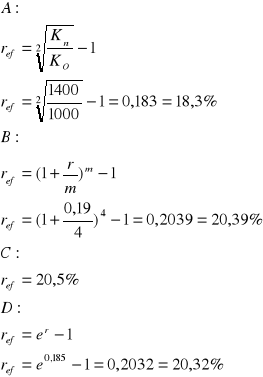
Najkorzystniej ulokować pieniądze w banku C
ref < r przy zastosowaniu rachunku odsetek prostych
ref > r przy zastosowaniu kapitalizacji m-razy (dziennej, miesięcznej lub kwartalnej)
ref > r przy zastosowaniu kapitalizacji ciągłej
Zadanie 3
Wpłacasz pewną kwotę na rachunek o stopie oprocentowania nominalnego 18% i kapitalizacji półrocznej. Po jakim czasie kwota na rachunku będzie dwukrotnie większa
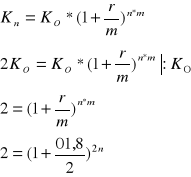
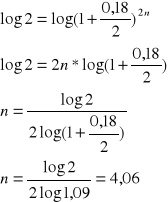
Zadanie 4
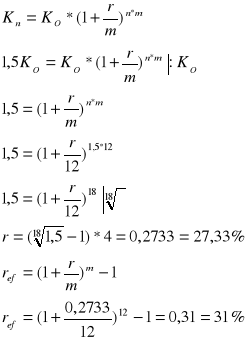
Ilość pieniędzy złożonych na rachunku wzrasta po półtora roku o 50% przy kapitalizacji miesięcznej. Jaka była by stopa nominalna i efektywna
Zadanie 5
Wpłacasz 100 zł na 5 lat. Jaka stopa efektywnego oprocentowania zapewni podwojenie oszczędności przy kapitalizacji kwartalnej
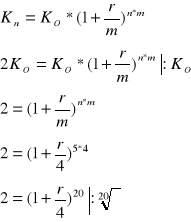
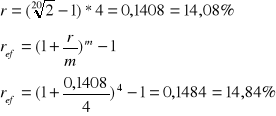
Zadanie 6
Pewien kapitał złożono na procent składany, kapitalizacja odsetek następuje, co kwartał a efektywna roczna stopa procentowa jest równa 33%. Ile wynosi zgodna stopa procentowa a ile nominalna stopa
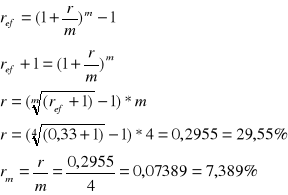
Zadanie 7
Na rachunku umieszczasz 100 zł, kapitalizacja kwartalna, stopa oprocentowania efektywnego 15%. Pieniądze wycofujesz po 8 miesiącach. Jaką kwotę otrzymasz
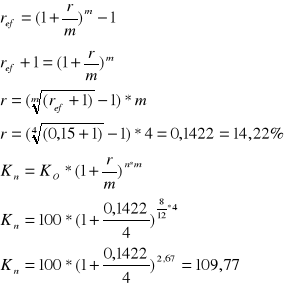
Zadanie 8
Po 3 latach na rachunku jest 1000 zł. Jaką kwotę wpłacono przy nominalnej stopie procentowej, 16% jeżeli kapitalizacja była?
roczna
ciągła
a)
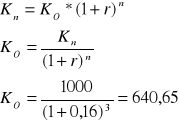
b)
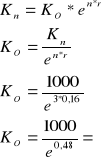
Rachunek oprocentowania składanego
Zadanie 1
Wyznaczyć nominalną stopę procentową dla kapitału w wysokości 2000 zł, który po dwóch latach przyniósł 500 zł odsetek przy rocznej stopie kapitalizacji.
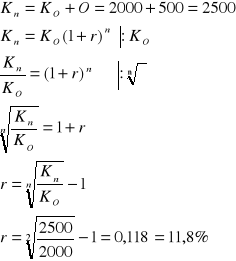
Zadanie 2
Wpłacasz 500 zł na 5 lat, jaka stopa oprocentowania efektywnego zapewni podwojenie Twoich oszczędności przy kapitalizacji tygodniowej.
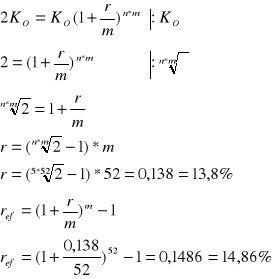
Zadanie 3
Bank zmienił oprocentowanie z 20% na 22%. Równocześnie wydłużył kapitalizacje z kwartału na pół roku. Czy prawdziwa jest informacja banku, że zmiana ta nie pogorszy sytuacji jego klientów.
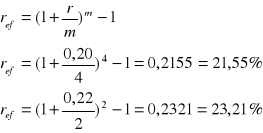
Stopa efektywna w drugim przypadku przy stopie nominalnej 22% i kapitalizacji półrocznej jest wyższa niż w przypadku pierwszym, tak więc sytuacja klienta nie została pogorszona.
Dyskonto handlowe i matematyczne
Zadanie 4
W jakim okresie czasu stopa dyskontowa wynosząca 20% i stopa procentowa 25% są sobie równoważne
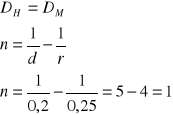
Tylko dla okresu 1 roku stopy te są sobie równoważne
Powyżej jednego roku DH > DM
Powyżej jednego roku DH < DM
Zadanie 5
Bank oferuje 17% oprocentowanie oszczędności w skali roku przy kapitalizacji kwartalnej. Jaka co najmniej powinna być stopa dyskontowa w skali roku zakupu papierów wartościowych, aby rentowność tej operacji była wyższa od rentowności lokaty bankowej?
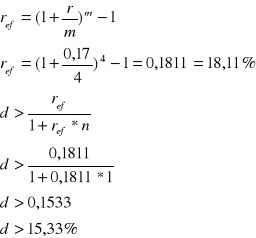
Zadanie 6
Jaka jest stopa procentowa (rentowność) oraz stopa dyskontowa zakupu za 900 papierów wartościowych o nominale 1000 zł i terminie jego wykupu za 5 miesięcy?
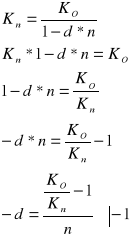
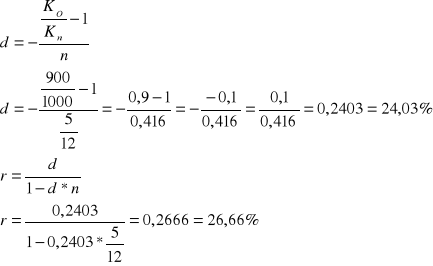
Zadanie 7
Za ile najmniej powinieneś kupić papier wartościowy o nominale 10000 zł i terminie wykupu 15 dni, aby osiągnąć rentowność 25%
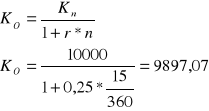
Zadanie 8
Możliwy jest zakup papieru wartościowego przy stopie dyskontowej 25% lub rentowności 30%. Na ile dni przed terminem wykupu ta druga możliwość jest korzystniejsza. Proszę wyznaczyć dyskonto handlowe i matematyczne dla okresu 120 dni przy wartości nominalnej 100 zł
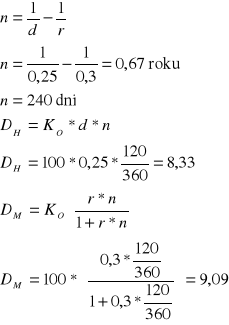
Dla okresu n < 240 wybór jest korzystny
Zadanie 9
Wyznaczyć stopę dyskontową, jeżeli dyskonto handlowe weksla o wartości nominalnej 100 zdyskontowanego na 30 dni przed terminem wykupu wynosi 2
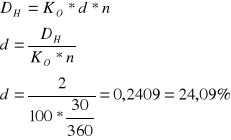
Zadanie 10
Firma otrzymała ofertę zakupu środka trwałego przy natychmiastowej zapłacie gotówką 4000 zł albo przy zapłacie 4800 za dwa lata. Firma ma możliwość uzyskania kredytu bankowego na okres 2 lat oprocentowanego 21% w skali roku przy kapitalizacji kwartalnej. Jaką decyzję powinno podjąć kierownictwo tej firmy?
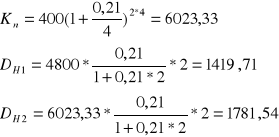
Firma powinna zapłacić za dwa lata kwotę 4800 zł.
Model rat równych przy kapitalizacji rocznej z dołu (bez wyprzedzenia) i z góry z (wyprzedzeniem)
Zadanie 1
Jaka będzie wartość 500 zł po 2 latach przy kwartalnych ratach z dołu oraz góry, jeżeli nominalna stopa procentowa wynosi 32%, a odsetki kapitalizowane są kwartalnie
W = 500
n = 2
m = 4
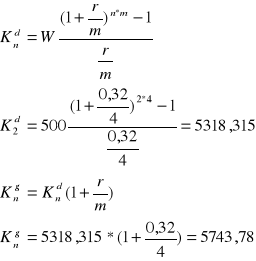
r = 32%
Zadanie 2
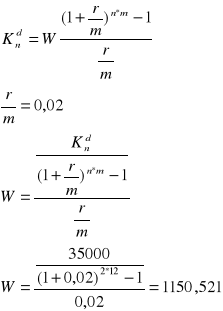
Cena samochodu wynosi 35000 zł, jakiej równej wysokości wkłady wnoszone na koniec kolejnych miesięcy pozwolą zgromadzić w ciągu 2 lat niezbędny fundusz na jego zakup. Bank stosuje miesięczną kapitalizację przy miesięcznej stopie procentowej wynoszącej 2%
Zadanie 3

Przy jaki okres czasu należy wpłacać z góry stałą kwotę 100 zł przy rocznej stopie procentowej 24% i kapitalizacji rocznej, aby uzbierać dokładnie 500 zł
Zadanie 4
Przez 5 lat będziemy otrzymywać rocznie 500 zł oblicz ile warte są te pieniądze obecnie jeśli:
płatności występują bez wyprzedzenia
płatności występują z wyprzedzeniem
Zakłada się, że nominalna stopa procentowa wynosić będzie 25%, a kapitalizacja ma miejsce jeden raz w roku
a)
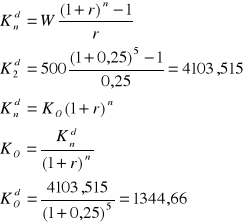
b)
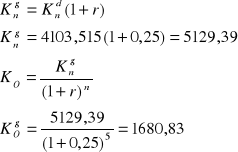
Wpłaty niezgodne
Kapitalizacja odsetek jest częstsza niż wpłaty
model rat równych przy kapitalizacji rocznej z dołu bez wyprzedzenia
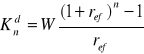
model rat równych przy kapitalizacji rocznej z góry z wyprzedzeniem
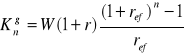
![]()
kapitalizacja śródroczna
kapitalizacja ciągła
![]()
![]()
np.
okres wpłat co kwartał a okres kapitalizacji co miesiąc czyli m = 3/1 = 3
okres wpłat co rok a okres kapitalizacji co pół roku czyli m = 1/0,5 = 2
![]()
Zadanie 5
Na koniec każdego półrocza wpłacano na konto kwotę 500 zł, wyznaczyć przyszłą wartość sumy wkładów oszczędnościowych po 4 latach, jeżeli bank stosuje kapitalizacje kwartalną przy rocznej stopie procentowej 16%
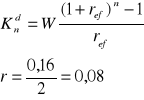
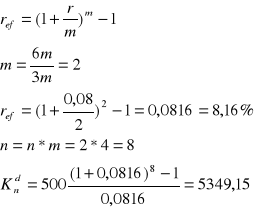
r = 0,08 dlatego że wpłaty są półroczne i roczną stopę procentową należy podzielić przez
Zadanie 6
Wpłacasz 300 zł co pół roku przy stopie procentowej 10% jaką kwotę otrzymasz po 3 latach jeżeli bank stosuje kapitalizację ciągłą wpłaty dokonywane są bez wyprzedzenia (z dołu)
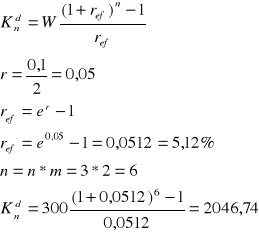
Zadanie 1
Zwracasz 10000 zł przy stopie procentowej 24% dług spłacisz z dołu w 8 miesięcznych równych ratach. Wyznacz kwotę raty jeżeli kapitalizacja odsetek jest:
dzienna
miesięczna
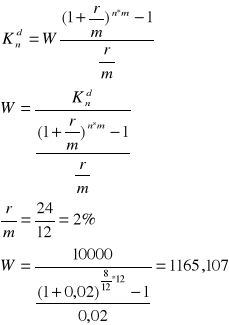
wpłaty niezgodne b) wpłaty zgodne

Zadanie 2
Lokujesz 10000 zł na 10 lat, stopa oprocentowania 17%, stopa inflacji 14%. Kapitalizacja na końcu roku. Jaką nominalną oraz realną kwotę będziesz dyskontować po podanym okresie
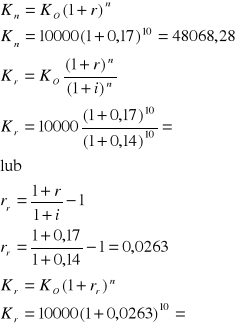
Zadanie 3
Lokujesz przez 10 lat po 100 zł
na początku każdego roku
na końcu każdego roku
Oprocentowanie wynosi 5%, inflacja 3,5%. Kapitalizacja na końcu roku. Jaką realną kwotę będziesz dysponować po tym okresie
a) b)
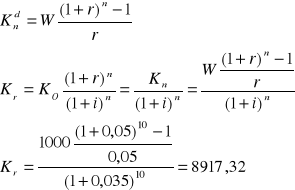
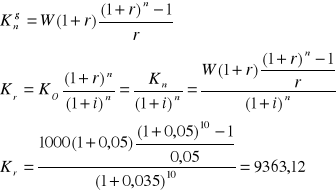
Szybsze rozwiązanie podpunktu b to wynik z podpunktu a podzielić przez (1+r)
Zadanie 4
Ile powinno się ulokować w banku, aby móc kupić za 5 lat mieszkanie o obecnej wartości 60000 zł, stopa procentowa dla oszczędności oferowana przez bank wynosi 16%, stopa inflacji (wzrost cen mieszkania) równa jest 9%, kapitalizacja raz w roku
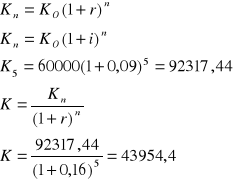
Zadanie 1
Sporządzić plan amortyzacji kredytu w wysokości 90000 zł oprocentowanego na 16% kredyt ten ma być spłacony w 6 równych kwotach płatności uiszczanych na końcu roku
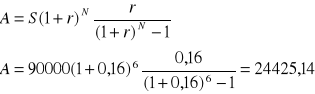
Kolejne lata |
Dług na początku okresu |
Rata kapitałowa |
Rata odsetkowa |
Kwota płatności |
Dług na koniec okresu |
1 |
90000 |
10025,14 |
14400 |
24425,14 |
79974,86 |
2 |
79974,86 |
11629,16 |
12795,97 |
24425,14 |
68345,70 |
3 |
68345,70 |
13489,83 |
10935,31 |
24425,14 |
54855,87 |
4 |
54855,87 |
15648,21 |
8776,93 |
24425,14 |
39207,66 |
5 |
39207,66 |
18151,92 |
6273,22 |
24425,14 |
21055,74 |
6 |
21055,74 |
21056,23 |
3368,91 |
24425,14 |
0 |
Σ |
|
|
56550,34 |
|
|
Rata odsetkowa = Dług na początku okresu * stopa procentowa
Kwota płatności = Rata kapitałowa + rata odsetkowa
Dług na koniec okresu = Dług na początku okresu - rata kapitałowa
Zadanie 2
Pewien przedsiębiorca zaciągnął kredyt w wysokości 2000 zł oprocentowanie nominalne kredytu 36% w skali roku kredyt ten należy spłacić w ciągu 4 lat w ratach kapitałowych o stałej wysokości płatnych na koniec każdego roku. Dokonać amortyzacji kredytu
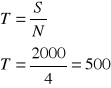
Kolejne lata |
Dług na początku okresu |
Rata kapitałowa |
Rata odsetkowa |
Kwota płatności |
Dług na koniec okresu |
1 |
2000 |
500 |
720 |
1220 |
1500 |
2 |
1500 |
500 |
540 |
1040 |
1000 |
3 |
1000 |
500 |
360 |
860 |
500 |
4 |
500 |
500 |
180 |
680 |
0 |
Σ |
|
|
1800 |
|
|
Rata odsetkowa = Dług na początku okresu * stopa procentowa
Kwota płatności = Rata kapitałowa + rata odsetkowa
Dług na koniec okresu = Dług na początku okresu - rata kapitałowa
Zadanie 3
Kredyt w wysokości 10000 zł ma zostać spłacony w 4 równych rocznych ratach kapitałowych. Stopa procentowa 14%. Kapitalizacja odsetek miesięczna. Ustalono że okres spłaty kredytu rozpoczyna się po upływie 2 lat od momentu jego zaciągnięcia. Sporządzić plan amortyzacji tego długu jeżeli karencję objęte są spłaty
kapitału i odsetek
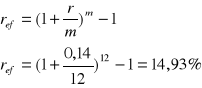
samego kapitału
Wzór ogólny na spłatę kredytu przy zastosowaniu karencji
![]()
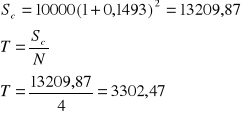
![]()
Wzór ogólny na spłatę kredytu przy zastosowaniu karencji w przypadku spłat niezgodnych
a)
Kolejne lata |
Dług na początku okresu |
Rata kapitałowa |
Rata odsetkowa |
Kwota płatności |
Dług na koniec okresu |
1 |
10000 |
- |
- |
- |
- |
2 |
- |
- |
- |
- |
13209,87 |
3 |
13209,87 |
3302,47 |
1972,23 |
5274,70 |
9907,40 |
4 |
9907,40 |
3302,47 |
1479,17 |
4781,64 |
6604,93 |
5 |
6604,93 |
3302,47 |
986,11 |
4288,58 |
3302,47 |
6 |
3302,47 |
3302,47 |
493,11 |
3795,57 |
0 |
Σ |
|
|
4930,61 |
|
|
Rata odsetkowa = Dług na początku okresu * stopa procentowa
Kwota płatności = Rata kapitałowa + rata odsetkowa
Dług na koniec okresu = Dług na początku okresu - rata kapitałowa
b)

Kolejne lata |
Dług na początku okresu |
Rata kapitałowa |
Rata odsetkowa |
Kwota płatności |
Dług na koniec okresu |
1 |
10000 |
- |
1493 |
1493 |
10000 |
2 |
10000 |
- |
1493 |
1493 |
10000 |
3 |
10000 |
2500 |
1493 |
3993 |
7500 |
4 |
7500 |
2500 |
1119,75 |
3619,75 |
5000 |
5 |
5000 |
2500 |
746,50 |
3246,50 |
2500 |
6 |
2500 |
2500 |
373,25 |
2873,25 |
0 |
Σ |
|
|
|
|
|
Rata odsetkowa = Dług na początku okresu * stopa procentowa
Kwota płatności = Rata kapitałowa + rata odsetkowa
Dług na koniec okresu = Dług na początku okresu - rata kapitałowa
Zadanie 4
Po 3 letnim okresie karencji obejmującym tylko raty kapitałowe dług w wysokości 80000 zł należy spłacać w jednakowych kwotach płatności po 30000 zł, bank stosuje kapitalizację roczną przy rocznej stopie procentowej 10%. Ułożyć plan spłaty długu

Kolejne lata |
Dług na początku okresu |
Rata kapitałowa |
Rata odsetkowa |
Kwota płatności |
Dług na koniec okresu |
1 |
80000 |
- |
8000 |
80000 |
80000 |
2 |
80000 |
- |
8000 |
80000 |
80000 |
3 |
80000 |
- |
8000 |
80000 |
80000 |
4 |
80000 |
22000 |
8000 |
30000 |
58000 |
5 |
58000 |
24200 |
5800 |
30000 |
33800 |
6 |
33800 |
26620 |
3380 |
30000 |
7180 |
6,25 |
7180 |
7180 |
179,73 |
30000 |
0 |
|
|
|
41359,73 |
|
|
W okresie 6,25 stopę procentową należy podzielić r/4
Rata odsetkowa = Dług na początku okresu * stopa procentowa
Kwota płatności = Rata kapitałowa + rata odsetkowa
Dług na koniec okresu = Dług na początku okresu - rata kapitałowa
Zadanie 5
Który z banków oferuje lepsze warunki do zaciągnięcia kredytu jeżeli w pierwszym banku stopa oprocentowania kredytu wynosi 20% a odsetki trzeba płacić co kwartał w drugim banku nominalna stopa procentowa wynosi 22% a odsetki należy płacić co pół roku
![]()
![]()
![]()
bank 1
bank 2
Lepsze warunki do zaciągnięcia kredytu oferuje bank 1
Zadanie 6
Bank udziela kredytów wg. stopy 20% przy miesięcznym poborze odsetek. Klient chciałby zaciągnąć kredyt w wysokości 5000 zł na okres 12 miesięcy spłacając go jednorazowo wraz z odsetkami na koniec jego trwania. Jeżeli bank zaakceptuje propozycję klienta to, jakie powinna być stopa tego kredytu, aby jego koszt nie odbiegał od standardowo udzielanych. Ile powinien zwrócić po upływie roku kredytobiorca
1
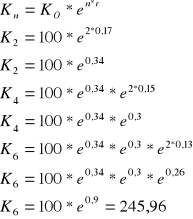
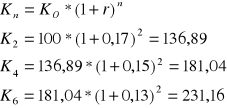
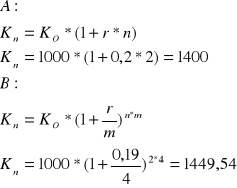
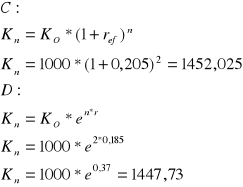
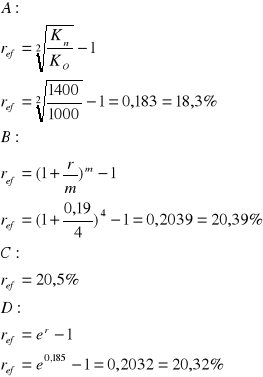
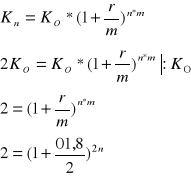
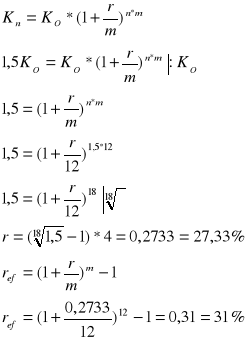
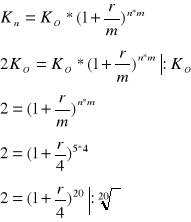
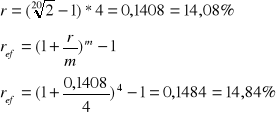
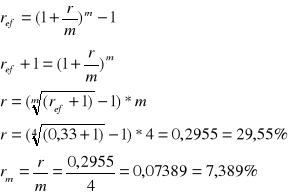
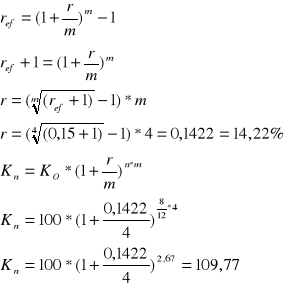
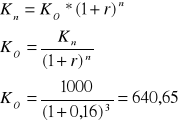
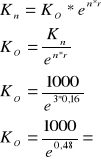
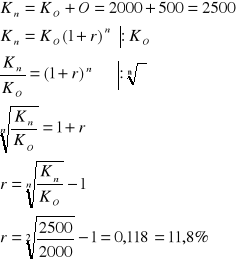
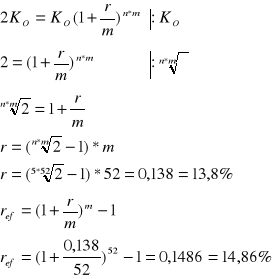
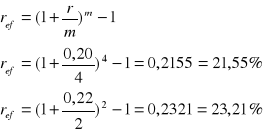
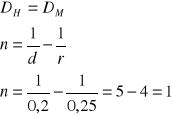

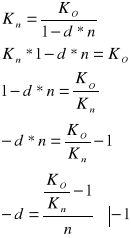
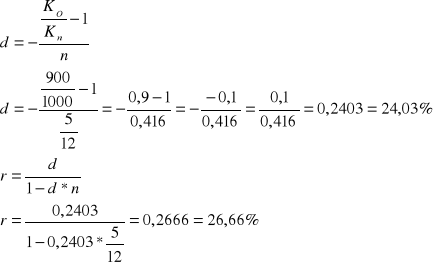
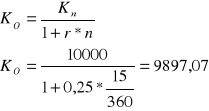
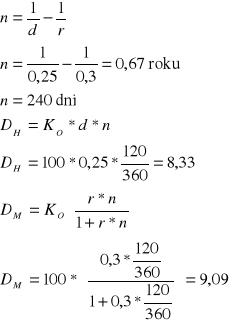
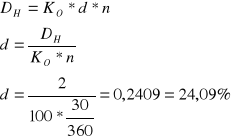
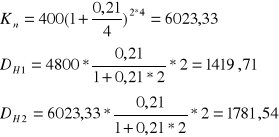
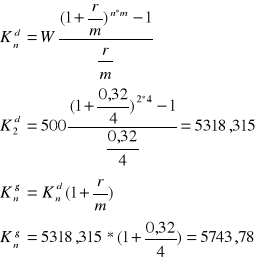
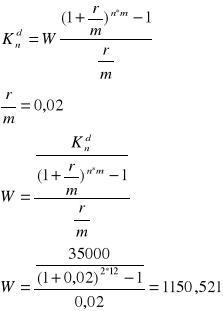

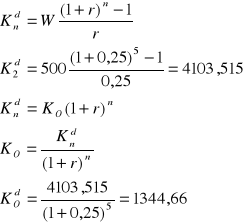
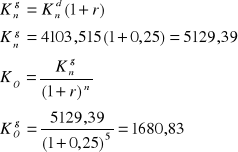
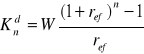

![]()
![]()
![]()
![]()
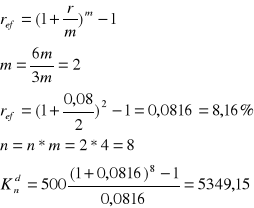
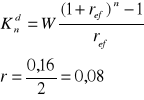
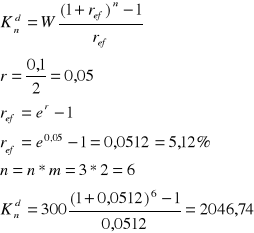
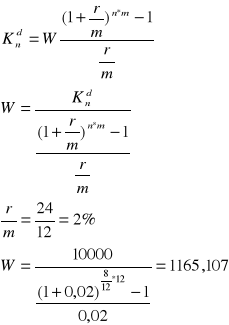
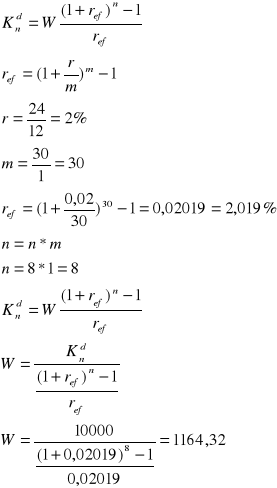
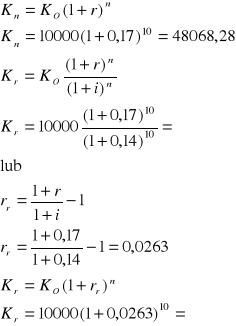
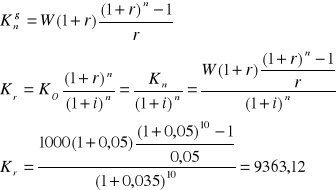


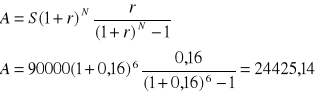
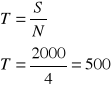
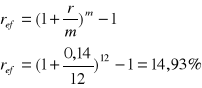
![]()
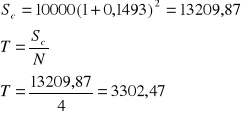
![]()
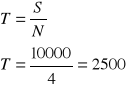

![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
,matematyka finansowa, wzory i zadania Rachunek odsetek prostych
Matematyka finansowa wzory i zadania (23 strony)
matematyka finansowa wzory i zadania (23 strony) id
,matematyka finansowa, wzory i zadania Rachunek oprocentowania składanego
,matematyka finansowa, wzory i zadania Dyskonto handlowe i matematyczne
Matematyka finansowa - wzory i zadania
matematyka finansowa wzory i zadania , kapital, odse
,matematyka finansowa, wzory i zadania Model rat równych przy kapitalizacji rocznej z dołu
,matematyka finansowa, wzory i zadania Wpłaty niezgodne
Matematyka finansowa wzory i zadania (23 strony
,matematyka finansowa, wzory i zadania Rachunek odsetek prostych
matematyka finansowa wzory i zadania (23 strony)
więcej podobnych podstron