Chi-kwadrat. Test zgodności
Test zgodności chi-kwadrat (inaczej zwany testem Pearsona) służy do porównania ze sobą zaobserowanego rozkładu naszej zmiennej z jakimś teoretycznym rozkładem. Jednakże przy testowaniu zgodności rozkładu naszej zmiennej z dobrze znanymi rozkładami teoretycznymi w statystyce : np. normalnym, Poissona zazwyczaj stosuje się inne testy np. test K-S, test Shapiro-Wilka.
Test zgodności chi-kwadrat w praktyce można wykorzystać na różne sposoby:
1) sprawdzenie równoliczności grup
2) porównanie występowania obserwacji z ich teoretycznym występowaniem
1) Równoliczność grup
Przykład:
Badacz chciał sprawdzić, czy w swoim badaniu była równa liczba kobiet i mężczyzn (statystycznie równa, nieistotne statystycznie różnice). W badaniu przebadał 480 mężczyzn oraz 520 kobiet. Wynik okazał się nieistotny statystycznie (dla p < 0,05). Oznacza to, że badacz może przyjąć, że przebadał podobną liczbę kobiet i mężczyzn (mówiąc językiem statystyki).
Test ten stosuje się również w przypadku sprawdzania, czy któraś z udzielanych odpowiedzi była najczęściej udzielana
2) Występowanie obserwacji a ich teoretyczne występowanie Przykład:
Załóżmy, że żyjemy w kraju, w którym 70% społeczeństwa stanowią kobiety. Badacz w swoim badaniu przebadał 60 mężczyzn i 40 kobiet. Następnie chciał sprawdzić, czy rozkład płci w jego badaniu pokrywa się z rozkładem w populacji danego kraju.
Teoretycznie, badając 100 osób, powinien zbadać 70 kobiet i 30 mężczyzn, aby odzwierciedlić proporcję w populacji. Przy użyciu testu zgodności chi-kwadrat stwierdził, że różnica w proporcji kobiet i mężczyzn jest na tyle duża, aby móc powiedzieć, że jego rozkład płci w jego badaniu nie odzwierciedla rozkładu w populacji.
Są dwa najważniejsze założenia testu zgodności chi-kwadrat: minimalna liczebność próby = 5 i niezależność grup
Sprawdzianem hipotezy zerowej jest statystyka wyrażona w następujący sposób:
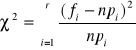
f - oznacza liczbę zaobserwowanych wartości z danego przedziału,
Statystyka testu ma rozkład χ2 o ν = k - r - 1 stopniach swobody, gdzie r to liczba szacowanych parametrów, od których zależy rozkład cechy w populacji, natomiast k to liczba przedziałów klasowych lub wariantów cechy X;
pi oznacza prawdopodobieństwo tego, że cecha X przyjmuje wartość należącą do i-tego przedziału klasowego, n⋅pi oznacza liczbę jednostek, które powinny znaleźć się w i-tym przedziale (przy założeniu, że cecha ma rozkład zgodny z hipotetycznym).
Jeżeli ![]()
, to nie ma podstaw do odrzucenia hipotezy zerowej, w przeciwnym przypadku istnieją podstawy do odrzucenia hipotezy zerowej.
Aby sprawdzić, czy wartość statystyki chi-kwadrat wskazuje na istotną statystycznie zależność, musimy sprawdzić, posługując się tablicą rozkładu chi-kwadrat, czy dana wartość wskazuje na istotne statystycznie różnice.
Aby tego dokonać, musimy znać:
wartość statystyki chi-kwadrat (wynik testu chi-kwadrat)
liczbę przebadanych osób
poziom istotności (poziom prawdopodobieństwa), dla którego dany wynik będzie wskazywał na istotną zależność
Dla przykładu, jeżeli przyjmiemy, że interesuje nas czy dany wynik jest istotny statystycznie, przy założeniu 5% szans popełnienia błędu przy wnioskowaniu (p = 0,05) i do tego wiemy, że zbadaliśmy 100 osób - to na skrzyżowaniu tych dwóch wartości odczytujemy wartość statystyki chi-kwadrat i porównujemy ją z uzyskaną w naszych obliczeniach statystyką.
Jeżeli wartość naszego testu będzie większa niż wartość z tablicy uznamy, że wynik jest istotny statystycznie (przy założeniu p = 0,05)
Jeżeli natomiast wartość naszego testu będzie mniejsza niż wartość z tablicy uznamy wtedy, że wynik nie jest istotny statystycznie.
Przykład:
Na podstawie danych zawartych w poniższej tablicy należy odpowiedzieć na pytanie czy na poziomie istotności 0,05 można sądzić, że rozkład dziennej liczby dostaw dla pewnego przedsiębiorstwa Z w ciągu 90 dni jest rozkładem Poissona?

Tab. Dzienna liczba dostaw dla przedsiębiorstwa Z
Przez X oznaczamy dzienną liczbę dostaw do przedsiębiorstwa Z.
Hipotezę zerową i alternatywną zapisujemy w następującej postaci:
H0: X ma rozkład Poissona,
H1: X nie ma rozkładu Poissona.
W rozkładzie Poissona wartości prawdopodobieństw są funkcją parametru m. Wartość parametru m jest nieznana, w związku z czym najpierw należy parametr ten oszacować na podstawie próby. Ponieważ w rozkładzie Poissona parametr m = E(X), można zatem do oszacowania tego parametru przyjąć estymator wartości przeciętnej. Otrzymujemy wartość średnią równą 1,656 stąd zaokrąglając przyjmujemy m = 1,7. Prawdopodobieństwa pi znajdujemy w tablicach rozkładu Poissona dla m = 1,7 tak, że pi = P(X = xi). Ostatnia wartość pi wynosi 0,092, jako różnica między jednością a sumą pi poprzednich.
Dzienna liczba dostaw (xi) |
Liczba dni (fi) |
xifi |
0 |
19 |
0 |
1 |
29 |
29 |
2 |
17 |
34 |
3 |
14 |
42 |
4 |
11 |
44 |
Suma |
90 |
149 |
|
|
|
wartość średnia |
1.656 |
|

W celu wyznaczenia statystyki testu χ2 należy dokonać pewnych obliczeń, które zawiera poniższa tablica:
Tab. Obliczenia pomocnicze
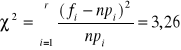
Wartość statystyki testu χ0,052 odczytana z tablic dla ν = 5 - 1 - 1 = 3 stopniach swobody wynosi 7,815.
Ponieważ χ2 < χ2α, to nie ma podstaw do odrzucenia hipotezy zerowej, że rozkład liczby dostaw jest rozkładem Poissona.
Rozkład chi kwadrat (zapisywany także jako χ²) to rozkład zmiennej losowej, która jest sumą k kwadratów niezależnych zmiennych losowych o standardowym rozkładzie normalnym. Liczbę naturalną k nazywa się liczbą stopni swobody rozkładu zmiennej losowej.
Jeżeli ciąg niezależnych zmiennych losowych
oraz:
to:
czyli słownie: Zmienna losowa Y ma rozkład chi kwadrat o k stopniach swobody.
Rys.1 Gęstość prawdopodobieństwa, dla różnych stopni swobody rozkładu zmienej losowej.
Filip Fornalik Wrocław 24.01.2010
172087
MBM


Wyszukiwarka
Podobne podstrony:
Opracowanie ekofizjograficzne, Studia - IŚ - materiały, Semestr 06, Systemy informacji przestrzennej
SPR-ANKI, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab2
sprawozdanie3, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab4
sprawozdanie oswietlenie, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab3
KWADRYKI, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab2
OpenGl, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab4
02.Protokoły, Studia PŚK informatyka, Semestr 5, semestr 5, moje, Pai, Projektowanie aplikacji inter
Zadania L3 I6X4S1, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab4
Zadania L3 I6Y3S1, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab3
tresc lab3 gk, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab3
Zadania L4 I6Y4S1, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab4
chi kwadrat, Inne, Studia, Wykłady Sędek - Statystyka
sprawko-pieci, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab2
Zadania L2 I6Y3S1, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab2
Zadania L3 I6Y4S1, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab3
Opała GK sprawozdanie lab4, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab4
Zadania L4 I6Y3S1, Studia, WAT Informatyka, s3 - GK - lab grafika komputerowa, Lab4
więcej podobnych podstron