FIZYKA
PYTANIA
1) POSTULATY MECHANIKI KWANTOWEJ.
![]()
1)Każdej wielkości fizycznej A przyporządkowujemy operator  Hermitowski, liniowy i posiadający zupełny okład funkcji własnych przy czym pomiędzy operatorami zachodzą takie relacje jak pomiędzy odpowiadającymi im wielkościami fizycznymi- reguła odpowiedzialności.
2) Możliwymi wynikami pomiaru wielkości fizycznej reprezentowanej operatorem A (Â) są wielkości własne tych operatorów α1, α2, α3......przy czym w wyniku pojedynczego pomiaru otrzymujemy tylko jedną wartość własną. 3) Jeżeli po dokonaniu pomiaru układ znalazł się w stanie opisanym jedną z funkcji własnych ϕ1, ϕ2,ϕ3 to
układu przed dokonaniem obserwacji opisuje funkcję
Ψ=∑cn ψn - kombinacja liniowa funkcji ψ z odpowiednio
n dobranym współczynnikiem C1, C2, C3
![]()
4) Wartość średnia wielkości fizycznej reprezentowanej operatorem A(A1) wynosi <α> ≡ <A>
5) Jeżeli na układach nie dokonujemy obserwacji to stan układu opisuje funkcja będąca rozwiązaniem równania Schrodingera. Iħ ∂ψ/∂t =Ĥψ
2) Postulaty Bohra (dla kwantowej budowy atomu).
Zostały one wysunięte przez Bohra w 1913r. i opisywały nowy kwantowy model budowy atomu. 1) Elektrony w atomach mogą krążyć tylko po pewnych dozwolonych orbitach, dla których moment pędu elektronu jest całkowitą wielokrotnością h czyli mvr = nh gdzie: m- masa elektronu, v- prędkość, r- promień orbity, h- stała Plancka
Elektron krąży po takiej orbicie nie emituje energii.
2) Atom może absorbować lub emitować promieniowanie w postaci kwantu energii E=hr przy przejściu z jednej orbity na drugą, przy czym E=εn1 -En2. En1,En2- energie elektronowe na tych orbitach . Bohr na podstawie tych postulatów wyznaczył teoretycznie promień atomu wodoru, którego wartość dobrze się zgadzała z wartością przewidywaną przez kinetyczną teorię gazów otrzymał też zgodny z doświadczeniem rozkładu linii poszczególnych serii widmowych wodoru oraz obliczył stałą Rytberga.
3) Zasada nieoznaczoności Heisenberga.
Jest konsekwencją falowo cząsteczkowej teorii materii. Zasada ta powstała ponieważ pewne cząstki ( elektrony, protony i inne) nie stosują się do praw fizyki klasycznej, lecz podlegają prawą mechaniki kwantowej. To ograniczenie dokładności pomiaru jest spowodowane falową naturą cząstek, na co nie można wpłynąć stosując coraz to dokładniejsze przyrządy. Najlepiej przedstawia to rysunek.
![]()
![]()
Jeżeli elektron przejdzie przez szczelinę o szerokości Δy na wysokości y to jego położenie będzie znane z błędu Δy. Elektrony mające właściwości falowe ulegają dyfrakcji na szczelinie. Na ekranie pozostają prążki dyfrakcyjne, co oznacza że elektrony po przejściu przez szczelinę padają w różnych punktach. Im więcej elektronów w danym miejscu tym większe natężenie obrazu. Elektron wychodzący ze szczeliny ma pewną składową prędkości w kierunku osi y oznaczoną Vy. Wartość tej składowej zależy od kąta ugięcia. Dla elektronu posiadającego swoją masę oznaczamy pęd w płaszczyźnie x, y, z. Dla płaszczyzny y ΔpyΔ≈ h -błąd pomiaru z obliczeń, Δpy- niepewność, znajomość pionowej składowej pędu, Δy- niepewność pionowej składowej położenia. Mierzymy py i y. Jeżeli chcemy zwiększyć dokładność pomiaru zmniejszamy szczelinę Δy, co powoduje zwiększenie szerokości prążków (zwiększenie kąta Q), co wiąże się ze zwiększeniem Δpy. Natomiast większa szczelina Δpy i zmniejszenie wartości prążków- zwiększa się niepewność Δϕ. W rzeczywistości błąd pomiaru jest jeszcze większy niż czasie powyżej. Stąd nierówność. ΔpxΔx≥h, ΔpyΔ≥h,
ΔpzΔ≥h. Zasadę tę w odniesieniu do położenia i pędu cząstki formułujemy: iloczyn niepewności pomiaru pędu i pomiaru położenia cząstki jest zawszenie mniejszy od stałej Planca.
4) Zasada zachowania pędu. W odniesieniu do pojedynczego punktu materialnego drugą zasadę dynamiki zapisalibyśmy F= dp/∂t. Dla układu punktów materialnych p0 =p1+p2+......
dp0/∂t=dp1/∂t+dp2/∂t+... ![]()
Wypadkowe wszystkich sił działających na układ punktów materialnych równe są pochodnej względem czasu pędu lub pochodnej względem czasu, wypadkowego pędu układu. Jeżeli wypadkowa wszystkich sil zewnętrznych działających na układ równa się zeru, wtedy dpw/∂t =0 a pw =const. Gdy wypadkowa wszystkich sił zewnętrznych działających na układ równa się zeru, to wektory wypadkowego pędu całego układu pozostają stałe. Zasada zachowania energii- w układach odosobnionych od zewnętrznego otoczenia w ten sposób, że energia w żaden sposób nie dostanie się do niego ani nie wyjdzie z niego. Całkowita wartość energii pozostaje niezmieniona. Mogą w nim zachodzić przemiany energetyczne jednej postaci w inną. Energia nie może być ani tworzona ani niszczona.
5) Zasada zachowania momentu pędu.
Do wyjaśnienia bierzemy pod uwagę pojedynczy punkt. Moment sił F1 działający na punkt materialny m masie m wyraża się wzorem M(F1)= m1r1α ⇒α=dw/dt ⇒M(F1)= m1r12 dw/dt `'r1''wprowadzamy jako stałą pod znak pochodnej d(r1ω)/∂t =dv1/∂t. Iloczyn r1m1v1 przedstawia αmomentu pędu względem czasu mają kierunki jednakowe wzdłuż osi obrotu bryły. Przechodząc z pojedynczego punktu wstępnie do całego ich zbiorowiska obracającego bryłę otrzymamy po lewej stronie równania wypadkowy moment siły, a po prawej stronie pochodną momentu bryły względem czasu.
Uwzględniając wektorowy charakter wielkości oraz wprowadzając dla momentu pędu symbol L otrzymamy Mw= dL/dt. Z równania wniosek, że gdy wypadkowy moment siły Mw równa się zeru to moment pędu pozostaje stały.
6) Równanie Bernuliego.
Dotyczy ono przepływu cieczy doskonałej przez przewody o zmiennym przekroju. Wiąże ciśnienie i prędkość przepływu z przekrojem. Przekroje s1, s2. Prędkości przepływu v1, v2 na wysokościach h1, h2 .
![]()
![]()
W1-W2+Ep1-Ep2 =Ek2-Ek1
W1=p1s1v1Δt W2=p2s2v2Δt
![]()
Ep1=mgh1 =s1v1Δt ςgh1 Ep2=mgh2=s2v2Δtςgh2
Ek1=mv12/2= ps1v1Δtv12/2 Ek2=mv22/2 =ps2v2Δtv22/2
s2v2Δt =s1v1Δt
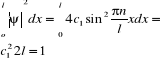
p1s1v1Δt - p2s2v2Δt + s1v1Δtςgh1 - s2v2Δtςgh =1/2 (ςs2v2Δtv22 -ps1v1Δtv12)
p1=p2 +ςgh1 -ςgh2 =1/2ςv22 -1/2ςv12
p1+ςgh1 +1/2 ςv12 =p2+ςgh2+ 1/2ςv22= const. Równ. Bernuliego
W1-W2 +Ep1-Ep2 =Ek2-Ek1
![]()
W1=p1s1v1Δt W=pm Ep=mgh Ek=mv2/2 m=svΔt
Przyrost energii jest równy pracy wykonanej przez różnicę sił działających na ciecz w przekroju s1,s2 wywołanych przez ciśnienie. W1-W2=Ep1-Ep2=Ek2-Ek1
W=psvΔt, Ep=mgh=svΔtςgh
Ek=mv2/2= ½ svΔtςv2 ς- jest to ro (symbol
gęstości)
7) Równanie Maxwella.
Opisuje ogół zjawisk elektromagnetycznych.
Zmienne pole magnetyczne wytwarza zmienne pole elektryczne, które może wywołać prąd elektryczny.
Prąd elektryczny lub zmienne pole elektryczne wytwarza zmienne pole magnetyczne.
Ładunek wytwarza pole elektryczne o indukcji odwrotnie proporcjonalnej do kwadratu odległości.
Nie istnieje w przyrodzie ładunek magnetyczny . Linie indukują się krzywymi zamkniętymi.
W celu uzyskania pełnego układu równań należy dołączyć podstawowe związki między wektorami elektrycznymi i magnetycznymi. D=εE, B=μH
8) Zjawisko Camptona.
Jest to zjawisko rozproszenia promieni X (Roentgena) na elektronach. Zaobserwował, że przedmiot naświetlany promieniami X staje się wtórnym źródłem promieni X. Foton padający, o energii hv0, uderza w spoczywający elektron e. Wskutek tego elektron zostaje odrzucony z prędkością v pod kątem α do pierwotnego kierunku foto nu, foton natomiast biegnie pod kątem β w stosunku do swego pierwotnego kierunku. Przy zderzeniu foton padający oddaje część swego pędu i energii elektronowi. Ponieważ energia fotonu jest związana z częstotliwością, więc zmniejszenie energii objawia się jako zmniejszenie częstotliwości, czyli zwiększenie długości fali. Z zasady zachowania energii otrzymujemy równość:
hv0 =hv+1/2mv2max hv- energia rozproszonego fotonu.
oznaczając pęd elektronu przez p a jego energię spoczynkową przez m0c2, a całkowita energię po zderzeniu przez E z zasady zachowania energii piszemy wzór.
hv=m0c2 =hv' + E, oraz z zasady zachowania pędu
hv/c =hv'/c cosϕ +pcosβ po przekształceniu
hv/c -hv'/c cosα =pcosβ hv'/c sinα =psinβ
TEORIA
1). Zasada nieoznaczoności.
Jest ona konsekwencją falowo-cząsteczkowej natury materii. Iloczyn niepewności pary wielkości fizycznych koniecznie sprzężonych jest nie mniejszy od stałej Plancka.
Δx∗Δpx≥h h- stała Plancka, h=6,6256e-34Js
dla zilustrowania tej zasady może posłużyć doświadczenie. Wyznaczamy położenie elektronu, oglądanego pod `'mikroskopem''. O zdolności rozdzielczej Δx=x/sinα, gdzie α to kąt apentury mikroskopu. W celu zmniejszenia Δx należy użyć światła o możliwie małej długości fali. Najmniejszym natężeniem światła potrzebnym do zobaczenia przez mikroskop elektronu jest jeden foton. Ponieważ rozproszony foton może wejść do mikroskopu w dowolnym miejscu wewnątrz kąta 2α, nieokreśloność Δpx pędu elektronu wynosi Δpx=pxsinα=h/λsinα
px=h/λ- pęd fotonu.
Nieokreśloność w równoczesnym określeniu pędu i położenia elektronu spełnia warunek: ΔxΔpx=λ/sinα
h/λsinα=ħ Δx0px≥h, ΔyΔpy≥h, ΔzΔpz≥h
ILOCZYN niepewności pędu i pomiaru położenia cząstki jest zawsze nie mniejszy od stałej Plancka. Jeżeli przez L oznaczymy moment pędu cząstki, a przez ϑ jej położenie kątowe, to ΔLΔϑ≥h co oznacza, że iloczyn niepewności pomiarów momentu pędu cząstki i jej położenia kątowego jest nie mniejszy niż `'h''. Jeżeli cząstka ma energię E, to dokładność ΔE jest zależna od czasu dokonywania pomiaru Δt zgodnie z nierównością ΔLΔα≥h, ΔEΔt≥h Oznacza to, że im dłużej cząstka zachowuje energię, tym dokładniej można tę energię wyznaczyć.
2). Studnia potencjalna.
Zakładamy, że cząstka porusza się wzdłuż osi x, lecz energia potencjalna U szatki zależy od x w następujący sposób: U(x)=0 jeżeli 0≤x≤l. Wykres funkcji U(x) tworzy U(x)=U0 jeżeli x<0 lub x>1 prostokątny dół zwany studnią potencjalną. Zakładamy, ze wysokość bariery potencjału jest nieskończenie duża (U0=∝). W takim wypadku cząstka o dowolnie dużej energii nie może opuścić jamy potencjalnej, stąd wynika, że prawdopodobieństwo znalezienia cząstki na zewnątrz jest równe zeru. Funkcja falowa musi być więc równa zeru na końcach przedziału (0, l), czyli ψ(0)=0 ϕ(l)=0—wart.,brzegowe
Równanie Schrodingera będzie opisywać f. płaską
4x=c1e2kx + c2e-2kx c1+c2=0 c1elkL+ c2e-lkL=0
obliczamy z pierwszego równania c2=4i, podstawiamy:
c1elkL -c1e-lkL=0 przechodząc do postaci trygonometrycznej mamy: kL=nπ n=±1,±2.... Energia cząstki w jamie:
Uwzględniając c2=-4 funkcja wygląda:
ψ=c1e2kx-c1e-2kx=2ic1sinkx=2ic1sin(nπx/l), c1 wyznaczamy z warunku
Ostatecznie funkcja falowa cząstki w j.p. wyraża się wzor
Energia cząstki znajdującej się j.p jest skwantowana. Dozwolone wartości energii nazywamy poziomami energetycznymi, a liczbę n- liczbą kwantową.
![]()
ψ(x) {ψ(x)}2 E
Funkcja gęstość poziomy
Falowa prawdopodo energetyczne
3). Efekt tunelowy.
Założenia E<U, bariera potencjalna o wys, U0 i szer a
Równanie Schrodingera w postaci ħ=h/2π
-(ħ/2m) (d2ϕ/dx2)+ U(x)ψ=Eψ Wartości energii potencjalnej dla obszaru : w I obszarze U(x)=o dla x<0
w II obszarze U(x) =U0 dla 0<x≤a, w III obszarze U(x)=0 dla x>a
W obszarze I i III równanie Schrodingera ma postać:
W obszarze II
Rozwiązując powyższe równanie otrzymamy ogólną funkcję ψ dla I ψ1=A1eikx+BIe-ikx
II ψII=AIIeHx+BIIe-Hx
III ψIII =AIII eikx+BIII e-ikx
Funkcja ψ będzie opisywać proces przejścia cząstki przez barierę potencjału wówczas, jeżeli funkcja ta oraz jej pochodne będą ciągłe w punktach x=0 i x=a, warunki te to:
(ψI)X=0 =(ψII)X=0 (dψI/dx)X=0 = (dψII/dx)X=0
(ψII)X=a =(ψIII)X=a (dψII/dx)X=a = (dψIII/dx)X=a
Z warunków tych wynika AI+BI=AII ,, AIIeHa+BIIe-Ha = AIIIeika , ikAI-ikBI=HAII-HBII , HAIIIeHa - BII-Ha =ikAIIIeika
Wyrażenie (AIII/AI)2 możemy interpretować jako prawdopodobieństwo tego, że cząstka padająca na barierę przejdzie przez nią = współczynnik przejścia
D=(AIII/AI)2 =2bk2H2/ (k2+H2)2 (eHa - e-Ha)2 +bk2H2
Prawdopodobieństwo tego, że cząstka odbije się od bariery nazywamy współczynnikiem odbicia R=1-D
Jeżeli bariera jest wysoka i szeroka, że He>>1, to wzór na D możemy zapisać:
4) Postulaty BOHRA.
W 1913 Niels Bohr zaproponował nowy kwantowy model budowy atomu. 1) Elektrony w atomie mogą krążyć tylko po pewnych `'dozwolonych'' orbitach, ale których moment pędu elektronu jest całkowitą wielokrotnością h, czyli mvr= ħ , gdzie m- masa elektronu, v- prędkość elektronu, r- promień orbity elektronu, ħ- stała Plancka. Elektron krążący po takiej orbicie NIE promieniuje energii. 2) Atom może absorbować lub promieniować promieniowanie w postaci kwantu energii E=hV (V- to ni), przechodząc z jednej orbity dozwolonej na drugą, przy czym E=En1 -En2 gdzie En1i En2 to energia elektronu na tych orbitach. Bohr na podstawie tych postulatów, wyznaczył teoretycznie promień atomu wodoru, którego wartość dobrze się zgadzała z wartością przewidzianą przez teorię kinetyczną gazów, otrzymał też zgodny z doświadczeniem rozkład lini poszczególnych serii widmowych wodoru oraz obliczył stałą Rydberga.
5) Równanie BERNULLIEGO.
Zakładamy, że ciecz płynie od przekroju S1 do S2 . Na górną powierzchnię S1 działa siła parcia F1 =p1S1 , na dolną powierzchnię działa siła F2=p2S2 . Siły w czasie dt wykonają pracę
F2v2dt-F1v1dt=p2S2v2dt-p1S1v1dt=(p2-p1)*V
V- rozważana objętość cieczy
Energia kinetyczna i potencjalna masy m cieczy zawartej w objętościach ograniczonych powierzchniami S1S1' orazS2S2' wynosi
(mv12 )/2+mgh1 (mv22 )/2+mgh2
gdzie h1 i h2 - wysokość położenia rozpatrywanych ob.jętości cieczy pod dowolnie wybranym poziomem.
Porównując pracę wykonaną przez siły F1 i F2 zprzyrostem energii strugii
(p2-p1)*V=mgh2+(mV22 )/2-((mV12 )/2+mgh1)
otrzymujemy równanie
(mV12 )/2+mgh1+p1V=(mV22 )/2+mgh2+p2V
Ponieważ rozważania dotyczą dwóch dowolnych odcinków strugi cieczy możemy zapisać
(mV2 )/2+mgh+pV=const.
Powyższe równanie nosi nazwę równania B, dzieląc stronami przez objętość V i podstawiając za mV gęstość cieczy ς (ro) mamy: ς+(ςv2)/2+ςgh=const.
[Suma energii poten., kinet. I ciśnienia jednostki masy ustalonego przepływu cieczy doskonałej jest wielkością stałą ].
6) PIERWSZA ZASADA TERMODYNAMIKI
1 cal - 4,186 J
U2-U1=Q+W
Q - energia pobrana (oddana) przez układ w wyniku wymiany ciepła
W - energia pobrana (oddana) przez układ w wyniku wykonania pracy przez siły zewnętrzne.
U2 - energia wew. w stanie kończącym.
U1- energia wew. w stanie początkowym.
Zmiana energii wew. układu termodynamicznego jest równa sumie ciepła pobranego (lub oddanego ) przez układ i pracy wykonanej nad układemprzez siły zew.
DU=dQ+dW
Własność ciał , która decyduje , czy dwa ciała zetknięte ze sobą są w równowadze termicznej czy nie nazywamy temperaturą. Temperatury ciał są jednakowe , jeżeli po zetknięciu pozostają one w równowadze termicznej.
7) II ZASADA TERMODYNAMIKI
1) Niemożliwy jest proces , którego jedynym wynikiem jest zamiana ciepła pobranego z grzejnicy na równoważną mu pracę , bez wprowadzenia zmiany w otoczeniu.
2) Niemożliwy jest proces , którego jedynym wynikiem jest przekazywanie energii w postaci ciepła od ciała o niższej temperaturze do ciała o wyższej temp., bez wprowadzenia zmian w otoczeniu.
8) III ZASADA TERMODYNAMIKI
W dowolnym procesie izotermicznym przebiegającym w pobliżu temperatury zera bezwzględnego zmiana entropii układu jest równa zeru, tzn. ΔS=0 dla T→0 albo S=So=const.
9) ENTROPIA
ENTROPIA (S) - termodynamiczna funkcja , nie zależna od drogi przejścia od jednego stanu do drugiego , a zależna tylko od początkowego i końcowego stanu układu. Entropia jest funkcją stanu określoną dla stanów równowagi i taką, że w procesie kwazistatycznym
dS=dQ/T S=∫dQ/T
Entropia układów termodynamicznych jest jednoznaczną funkcją stanu tych układów.
σ=ds/dt W rzeczywistych procesach fizycznych źródło entropii jest zawsze dodatnie i jest równe zeru tylko w stanie równowagi σ≥0 ds=dQ/T
10) ZAKAZ PAULIEGO.
W atomie zachodzi wzajemne oddziaływanie elektronów. Powoduje to trudności w obliczaniu energii i poszczególnych elektronów , ale ich energie związane są z liczbami kwantowymi. Każdy elektron w atomie scharakteryzowany jest przez 4 liczby kwantowe :
główna : n=1,2,3...,∞
orbitalna: l=0,1,2,...,n-1
magnetyczna: m=0,±1, ±2,..., ±(l-1), ±l
spinowa: s=±1/2
Zespół tych czterech liczb charakteryzuje stan kwantowy elektronu. Elektrony znajdujące się w danym atomie obowiązuje ZAKAZ PAULIEGO:
Elektrony w atomie muszą się różnić chociaż jedną liczbą kwantową lub , inaczej dowolne dwa elektrony w atomie nie mogą znajdować się w tym samym stanie kwantowym.
11) WZÓR PLANCKA.
Pierwszym z licznego grona badaczy, któremu udało się rozwiązać poprawnie zagadnienia promieniowania ciała doskonale czarnego był Max P. założył on mianowicie, że energia przypadająca na jeden stopień swobody oscylatora nie jest równa kT, lecz całkowitej liczbie r pomnożonej przez bardzo małą porcję energii ε, oraz że liczba oscylatorów nm o energii rε podlega rozkładowi Bolzmana, czyli
Energia nm wynosi
Średnia energia pojedynczego oscylatora to:
Wprowadzając x=exp(-ε/kT)
12) Przemiany gazu doskonałego.
W przemianach termodynamicznych działają siły niezachowawcze. IZOTERMICZNA- w przemianie tej T=const. Z równania Clapeyrona wyznaczamy p=nRT/V
![]()
Ponieważ w procesie izotermicznym temperatura pozostaje stała, a więc również nie ulega zmianie energia wewnętrzna zatem dU=0. IZOBARYCZNA- tu tej p=cons.
Pracę tę możemy bezpośrednio obliczyć z wzoru:
W przemianie izobarycznej ciepło właściwe cp= const, zatem doprowadzone ciepło dQ=ncpdT
IZOCHORYCZNA- V=const, zatem V1=V2 i praca sił ciśnienia jest równa zeru. Czyli dW=pdW =0 zaś izochoryczne ciepło właściwe cV =const, skąd dQ=dU=mcVdT
Dla przemiany izochorycznej I zasada termodynamiki dU =dQ-pdV można napisać w postaci: dQ=dU +pdV= d(U+pV) stąd wynika, że ilość ciepła pobrana (lub oddana) przez układ jest równa zmianie wielkości H=U+pV zwanej eutalpią. ADIABATYCZNA- przemiana bez wymiany ciepła z otoczeniem (dQ=0). Stosując I zasadę do jednego mola gazu doskonałego i piszemy:
CVdT=-pdV, cVdT=-RT/V dV /:cVT mamy dT/T= (-R/cV )dV/V wynika lnT =-R/cVlnV +const
pV=const. Z równań tych wynika, że podczas tej przemiany zmieniają się wszystkie trzy parametry p,V,T.
![]()
13) CYKL CARNOTA.
Rozważania dotyczą maszyny wyidealizowanej, w której procesy są odwracalne. Maszyna ta wykonuje zamknięty cykl, po pewnej liczbie przemian wraca do stanu początkowego. Ciałem, które podlega pr., cyklicz jest gaz doskonały. Składa się z czterech cykli: 1) Rozprężanie izotermiczne w temp., T1, 2) Rozprężanie adiabatyczne przy zmianie od T1 do T2, 3) Sprężanie izotermiczne w temp. T2, 4) sprężanie adiabatyczne od T2 do T1.
P1(V1T1), P2(V2T2), P3(V3T4), P4(V4T3)
|
Rozprężanie izoter |
Rozp. adiabat |
Spręż izoter |
Spręża adiaba |
Zmiana objętości |
V1→V2 |
V2→V3 |
V3→V4 |
V4→V1 |
Zmiana tem. |
T1=const. |
T1⇒T2 |
T2=const |
T2→T1 |
Praca wyko nana |
W1=RT1* lnV1/V2 |
W2=C0* (T2-T1) |
W3=-RT *lnV4/V3 |
W4=Cv* (T1-T2) |
Ciepło pobr ane |
Q1 |
0 |
Q2 |
0 |
![]()
Proces adiabatyczny (II i IV) możemy zapisać:
Otrzymujemy: (V3/V4)H-1=(V2/V1)H-1 czyli V3/V4 = V2/V1
Praca wykonana przy procesie izotermicznym III
W3=RT2ln(V3/V4) W3=-RT2ln(V1/V2) czyli W1=-W3
Suma prac w procesach adiabatycznych jest równa zeru
W=W1+W3 =R(T1-T2)ln(V1/V2). Z pierwszej zasady termo., dla przemiany izotermicznej gazu doskonałego mamy W=-Q ,W1=RT1ln(V1/V2)=-Q1
I analogicznie W3=-RT1ln(V1/V2)=Q1-Q2
W=W1+W3=R(T1-T2)ln(V1/V2)=-(Q1+Q2)
![]()
14) SERIE WIDMOWE ATOMU WODORU.
Jedna z podstawowych dróg poznania struktury atomów dowolnego pierwiastka jest badanie wysyłanego lub absorbowanego promieniowania. Pierwiastki w postaci gazu lub pary wysyłają promieniowanie o charakterystycznym widmie złożonym z ostrych lini. Badamy je za pomocą spektrometrów lub spektroskopów. Najprostszą budowę ma atom wodoru, co odzwierciedla się w postaci widma. W widmie atomu wodoru mamy następujące serie: Lymanna (ultrafiolet), Balmera (widzialne), Paschena (podczerwień), Bracheta, Pfunda,
Zapis serii widmowych w podobnej postaci był podany po raz pierwszy przez Balmera (1885) dla serii widmowej wodoru nazwanej jego imieniem.
15) FUNKCJA FALOWA.
Cząstkom trzeba przypisać właściwości falowe. F.F. jest ogólnie biorąc funkcją współrzędnych punktu w przestrzeni oraz czasu: Ψ(x,y,z,t). Może przyjmować wartości zespolone, istotne znaczenie ma kwadrat modułu F.F.
Kwadrat modułu F.F. Ψ(x,y,z,t) jest równy gęstości prawdopodobieństwa p(x,y,z,t) znalezienie cząstki w chwili t i w punkcie przestrzeni o współrzędnych (x,y,z) zatem Ψx Ψ=Ψ=p p=pΔV=Ψ2ΔxΔyΔz
Zgodnie z def., prawdopodobieństwa całka z gęstości prawdopo., po objętości całej przestrzeni, w której znajduje się cząstka jest równe jedności
F.F. stanowi rozwiązanie
pewnego równania różniczkowego, zwanego równaniem Schrodingera. Poniżej przedstawiam prostszą jego formę niezależną od czasu.
gdzie
energia całkowita cząstki, U(x,y,z)- energia potencjalna cząstki zależna od jej położenia. Używając pojęcia liczby falowej
Równanie Schrodingera zapisujemy: ∇2Ψ+k2Ψ=0
Przy czym liczba k nie jest stałą i zależy od współrzędnych określających położenie cząstki. Rozwiązanie równania Schrodingera polega na znalezieniu postaci funkcji falowej i wartości energii cząstki E, zależy zatem od rozkładu energii potencjalnej U(x,y,z), która określa siły działające na cząstkę.
16) RÓWNANIE SCHRODINGERA
Nie da się go wyprowadzić . Rangę ma taką jak II zasada dynamiki . Jest to zapis prawa przyrody.
1) przypadek gdy cząstka nie ma energii potencjalnej ( jeden wymiar )
E=Ek=1/2*mvx2=px2/2m x,U=0
U=Ep energia potencjalna
EΨ= px2/2mΨ ∂Ψ/∂t= -i/ ħ*EΨ ⇒ EΨ= iħ* ∂Ψ/∂t
∂Ψ/∂X= i/ ħ*pxΨ ∂2Ψ/∂X2=( i/ ħ*px)2Ψ= -px2/ħ2*Ψ ⇒
px2/2m *Ψ = -ħ2/2m *∂2Ψ/∂X2
i ħ*∂Ψ/∂t= -ħ2/2m*∂2Ψ/∂X2
E→Ệ= i ħ*∂/∂t operator energii
px2→ -ħ2*∂2/∂x2
2) (x,y,z) U=0 przypadek trójwymiarowy
cząstka swobodna
3) (x,y,z) U≠0 przyp., trójwymiarowy ogólny
17) PRAWO GAUSSA.
![]()
D- indukcja elektryczna, E natężenie pola
Elementarny strumień przez element powierzchni.
Gdzie α- kąt miedzy wektorami D i ds., a Dn składowa D prostopadła do powierzchni.
Strumień indukcji ΦD przez dowolną powierzchnię zamkniętą jest równy całkowitemu ładunkowi ∑q zawartemu wewnątrz tej powierzchni
PRAWO GAUSSA dla pola magnetycznego
![]()
Strumień indukcji magnetycznej przez
dowolną powierzchnię zamkniętą jest równy zeru.
18) PRAWO KIRCHOFFA.
I w dowolnym węźle obwodu sumą algebraiczną natężeń prądów wpływających i wypływających z węzła równa się zero, czyli.
II W dowolnym oczku obwodu suma algebraiczna wszystkich sił elektromotorycznych i spadków napięć jest równe zer, czyli:
19) DRGANIA CHARMONICZNE.
![]()
![]()
![]()
![]()
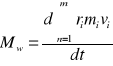
![]()
![]()
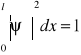
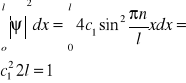
![]()
mE
/
)
(
2mm
0
2
2
U
E
dx
Y
d
![]()
h
k
2
2
H
h
m
U
E
0
2
2
(
)
(
Ha
H
e
H
k
k
D
2
2
2
2
2
*
16
2
)
sin(
/
2
l
x
n
l
n
0
Bds
dt
d
Hdt
0
dt
d
Edt
B
![]()
kT
r
n
n
m
exp
0
0
exp
m
r
n
r
n
r
kT
(
(
00
0
0
0
0
/
exp
/
exp
0
r
n
r
kT
r
n
kT
r
n
r
..
1
..
3
2
1
2
2
x
x
x
x
x
2
1
V
V
pdV
W
![]()
2
1
2
1
2
1
ln
ln
V
V
V
V
V
V
nRT
V
nRT
V
dV
RTn
W
)
(
2
1
2
1
V
V
p
dV
p
W
V
V
Q
Q
Q
2
1
![]()
1
2
1
2
1
1
2
1
2
1
1
ln
ln
)
(
T
T
T
V
V
RT
V
V
T
T
R
W
W
1
2
dV
(
0
,
,
8
2
2
2
z
y
x
U
E
h
m
2
2
2
2
2
2
2
z
y
x
δ
δ
δ
δ
δ
δ
)
(
2
4
2
2
2
2
2
U
E
mE
h
h
p
h
k
k
∂
∂
∂
∂
∂
∂
∂
∂
2
2
2
2
2
2
2
2
z
y
x
m
t
i
2
2
i
t
m
U
∂
∂
U
m
H
2
2
![]()
![]()
∂
∂
H
t
i
∂
∂
∂
∂
∂
∂
2
2
2
2
2
2
z
y
x
![]()
E
D
s
D
Dds
D
d
Dds
D
n
d
D
ds
D
ds
cos
a
DS
D
cos
q
Dds
D
n
i
Ii
1
0
n
i
n
i
IiRi
i
1
1
0
Wyszukiwarka
Podobne podstrony:
mała ściąga, AM SZCZECIN, FIZYKA, FIZYKA-WYKŁADY, Egzamin
this, AM SZCZECIN, FIZYKA, FIZYKA-WYKŁADY, Egzamin
Fizyka-caly, AM SZCZECIN, FIZYKA, FIZYKA-WYKŁADY, Egzamin
fizyka1, MIBM WIP PW, fizyka, Fizyka - wykład egzamin, idmt22
Fizyka 11, MIBM WIP PW, fizyka, Fizyka - wykład egzamin, idmt22
Automatyka - 5-3 - Elementy inercyjne, AM SZCZECIN, AUTOMATYKA, Automatyka - wykłady
Pan Ziemniak, AM SZCZECIN, AUTOMATYKA, Automatyka - wykłady, Automatyka Okrętowa Kaszycki
AUTOMATYKA-WYKŁADY-KUROWSKA- bez miejsc na rysunki, AM SZCZECIN, AUTOMATYKA, Automatyka - wykłady
Automatyka - 5-2 - Sygnały deterministyczne, AM SZCZECIN, AUTOMATYKA, Automatyka - wykłady
AUTOMATYKA-WYKŁADY-KUROWSKA, AM SZCZECIN, AUTOMATYKA, Automatyka - wykłady
Automatyka - 5-3 - Elementy inercyjne, AM SZCZECIN, AUTOMATYKA, Automatyka - wykłady
fizyka pytania egzaminacyjne, materiały air, fizyka dla elek, wykład 1
Fizyka 2, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Wykład, EGZAMINY z zeszłych l
Egz1DDD-2010, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Wykład, EGZAMINY z zeszły
Fizyka 2, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Wykład, EGZAMINY z zeszłych l
Egz1CCC-2010, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Wykład, EGZAMINY z zeszły
zag-2010, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Wykład, EGZAMINY z zeszłych l
więcej podobnych podstron