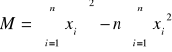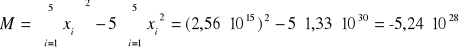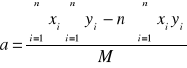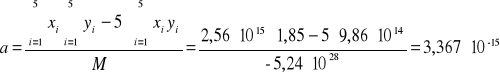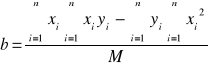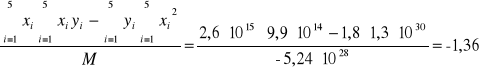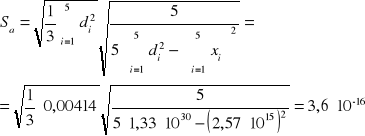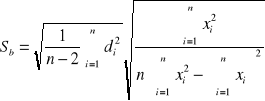Sprawozdanie z ćwiczenia nr 29.

Michał Tyszko

Marcin Wróblewski

Badanie efektu fotoelektrycznego zewnętrznego.

Teoria:

Celem tego ćwiczenia było wyznaczenie stałej Planck'a i pracy wyjścia elektronu podczas obserwacji efektu fotoelektrycznego. Do pomiarów wykorzystywaliśmy fotokomórkę (próżniową bańkę szklaną z dwoma elektrodami), filtry interferencyjne, źródło światła, potencjometr, woltomierz i amperomierz.

Efekt fotoelektryczny zewnętrzny jest jednym ze sposobów oddziaływania fali elektromagnetycznej (także światła) z materią. Zjawisko to polega na wybijaniu elektronów z powierzchni metalu przez padającą wiązkę światła o odpowiedniej częstości. Promieniowanie świetlne powoduje emisję elektronów z metali i dlatego nazywane jest efektem fotoelektrycznym. Potencjałem hamowania (V_h) nazywamy taką wartość napięcia na ujemnie naładowanej anodzie, dla której wartość natężenia prądu jest równa zero. Prąd fotoelektryczny maleje w miarę obniżania częstotliwości i znika przy wartości progowej częstości, której odpowiada progowa długość fali ( c/ Część energii, którą wybity z fotokatody otrzymał od światła jest zużywana na wykonanie pracy wyjścia, a reszta zamienia się w energię kinetyczną. Zjawiska efektu fotoelektrycznego nie można interpretować na gruncie falowej teorii światła, dlatego jest ono interpretowane w odniesieniu do fotonowej teorii zjawiska fotoelektrycznego stworzonej przez A. Einsteina. Według tej teorii światło traktujemy jako strumień fotonów o energii h (stała Plancka, -częstotliwość światła). W tej interpretacji efekt fotoelektryczny jest zderzeniem fotonu i elektronu uwięzionego w metalu i możemy dla tego zderzenia zapisać zasadę zachowania energii: h  W + E_max . Wiemy także, że energia maksymalna kinetyczna jest równa eV_h.

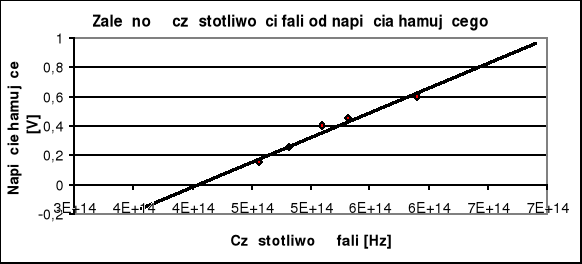
Teoria Einsteina przewiduje liniowy związek między potencjałem hamowania, a częstotliwością padającego światła wyrażony wzorem:

Na podstawie tych wniosków przyjęto, że światło posiada cech zarówno falowe jak i korpuskularne, dlatego w pewnych warunkach zachowuje się jak fala, a w innych jak foton. Stwierdzono, że własności falowe dominują przy dużych długościach fali, a cząsteczkowe przy małych, gdy rośnie energia fotonu.

Wykonanie ćwiczenia:

Wyniki pomiarów potencjału hamowania przy znanej długości fali przedstawiliśmy w poniższej tabeli.

 [nm]	 [Hz]	Uh śr [V]	I [nA]
657	4,6	0,15	0
622	4,8	0,25	0
589	5,1	0,4	0
564	5,3	0,45	0
508	5,9	0,6	0

Po przeliczeniu długości fali na jej częstotliwość korzystając ze wzoru   c/ wyniki umieściliśmy w tabeli i nanieśliśmy na wykres. Przez otrzymane punkty poprowadziliśmy prostą tak, że na osi y odłożyliśmy wartości potencjału hamowania, a na osi x częstotliwość fali.

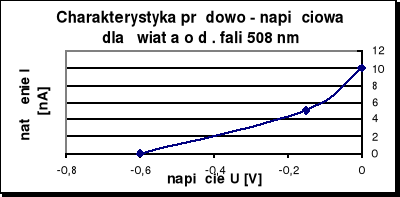
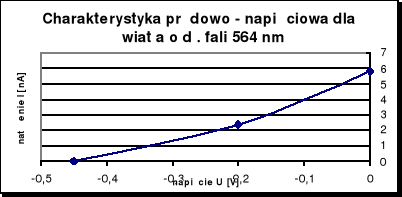
Charakterystyki prądowo - napięciowe dla każdej długości fali przedstawiają poniższe wykresy.

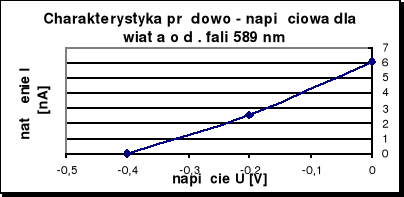
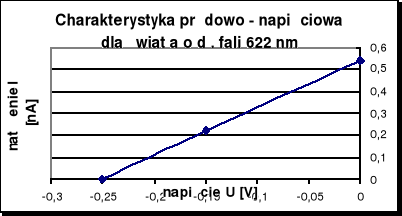
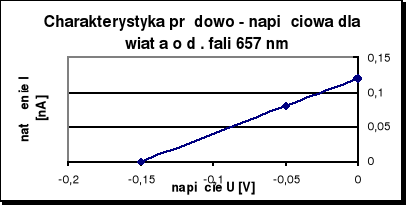
Obliczenia:

Korzystając z metody najmniejszych kwadratów i przy jej pomocy wyznaczamy parametry a i b szukanej prostej oraz ich błędów. Równanie prostej wyraża się wzorem:

tak więc:

;
;

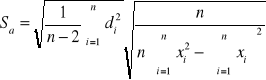
Metoda najmniejszych kwadratów szacuje parametry prostej takiej której kwadraty odchyleń od wyznaczonych punktów są najmniejsze. Po rozwiązaniu układu równań i korzystając z metody najmniejszych kwadratów otrzymujemy poniższe wartość parametrów a i b oraz ich błędy (odchylenia standardowe).

Korzystając z uproszczeń wyliczamy.

wówczas:

Reasumując obliczenia otrzymujemy, że:

a =

b = -1,36

S(a) =

S(b) =

Otrzymujemy więc korzystając z tych samych zależności co poprzednio, że :

Wynik otrzymanej pracy podajemy też w elektronowoltach.

Rachunek błędu:

Obliczenia zostały wykonane z uwzględnieniem rachunku błędu przy wykorzystaniu wzorów na najmniejszą sumę kwadratów. Wszelkie błędy grube zostały pominięte.

Wnioski:

Otrzymane przez nas wartości stałej Plancka są w bardzo dużym przybliżeniu równe wartości umieszczonej w tablicy, czyli

Wielkość h przez nas otrzymana nie pokrywa się z wartością tablicową, tj.
, możemy zatem wysnuć wniosek, że wystąpiły czynniki niepozwalające dokładnie wyznaczyć stałej h. Tymi czynnikami mogą być zbyt duże niedokładności przy wyznaczaniu potencjału hamowania, zwłaszcza przy wykorzystaniu przesłon przepuszczających światło o dużej długości fali. Innymi słowy częstotliwość tego światła jest mała a zatem również mała energia fotonu. Fotony o niewielkiej energii dają prąd o niedużym natężeniu - potencjał hamowania ma mniejszą wartość dlatego błąd względny jest duży. Dodatkową przyczyną jest niedokładność przyrządów pomiarowych czułych na bardzo małe prądy, co w efekcie zbliżenia nawet ręki do takiego przyrządu, powoduje niedokładności pomiarowe.

3