EKONOMETRIA - WYKŁADY.

Wykład z dnia 23.03.2012 r.

Model wielorakiej i parzystej regresji liniowej.

Podstawowym zagadnieniem regresji jest znalezienie więzi między różnymi parametrami ekonomicznymi.

Na mikro- i makro- poziomach a także studiowanie, oddziaływanie mniej ważnych parametrów na inne, bardziej istotne parametry na mikro- i makro- poziomie.

Wprowadzimy następujące oznaczenia:

x₀ , y decyzyjne zmienne (zmienne objaśnione)

zmienne faktorowe (zmienne objaśniające)

Będziemy przypuszczać ,że zależności między decyzyjnymi i faktorowymi zmiennymi są spisane przez funkcję:

(1)

(2)

parametry strukturalne - niewiadome.

składniki losowe dla których wartość oczekiwania = 0 i niewielka dyspersja.

Dalej przypuszczamy, że zależności między decyzyjnymi faktorowymi zmiennymi dość dobrze. Może być przedstawiona za pomocą modeli liniowych:

(3)

(4)

O ile wartość oczekiwania = 0 wtedy inna postać wzoru 3 i 4 ,są następujące wzory:

(5)

(6)

Równanie 5 nazywa się liniowym wielorakim równaniem regresji, a równanie 6 - parzystym równaniem liniowym regresji.

W równaniach 5 i 6 wyjściowe swe dane
y są wektorami, które mają postać:

			…
			…
			…
			…

. . .	. . .

Tutaj n - pojemność (próbki) informacji wyjściowej, dlatego żeby równanie regresji było reprezentatywne, tzn. wzbudzające zaufanie w badaczu koniecznie jest spełnieniem warunku

(7)

Czyli im większe różnice n 3p tym jest większe zaufanie do modelu regresji.

Podstawową istotą metody najmniejszych kwadratów jest to, że niewiadome parametry
są wyznaczone na podstawie następującego warunku:

(8)

Jeżeli wzór 5 podstawimy do 8 mamy:

(9)

Warunek 8 ma następujące interpretacje:

Suma kwadratów odchyleń teoretycznych wartości decyzyjnej zmiennej X_0i pod empirycznych wartości X_0i musi dążyć do minimum.

Z kursu matematyki, wiadomo, że funkcja z wieloma zmiennymi (9) będzie przyjmować wartości minimalne w tym punkcie, - którym pochodzą cząstkowe po odpowiednich zmiennych są równe 0 . Tzn. że niewiadome parametry
są rozwiązaniem następującego układu równań:

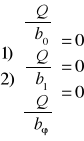
(10)

Po wykonaniu operacji różniczkowania w układzie równań 10 otrzymujemy:

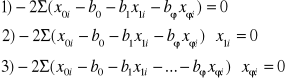
(11)

Po prostych transformacjach w układzie równań 11 otrzymujemy układ równań:

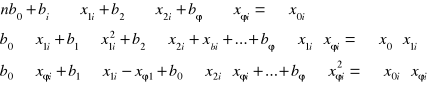
(12)

Układ równań 12 nazywa się normalnym układem równań dla znalezienia niewiadomych parametrów

Dla znalezienia rozwiązania układu równań 12 najczęściej są wykorzystywane metody Gausa i Kramela.

Rozpatrzymy teraz szczególne wypadki układu równań 12.

(13)

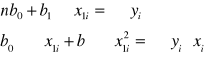
(14)

(15)

Dla znalezienia niewiadomych parametrów b₀ , b₁, b₂ .

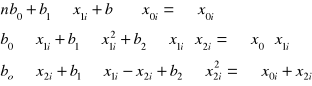
(16)

Parametry równań regresji
mają pełną interpretację ekonomiczną.

Wartości współczynnika regresji b_i pokazuje nam na ile jednostek zwiększy się jeśli b_i > 0, czyli zmniejszy się b_i < 0 wartość średniej decyzyjnej zmiennej X₀ wartość czy zwiększenie zmiennej X_i o 1 jednostkę i przy pewnej stałej
X₁ , X₂ , …, X_i-1 , X _(-1)

X_i x 1

Dla współczynnika regresji b₀ nie ma interpretacji ekonomicznej. Wartości współczynnika regresji wskazują nam, że przy zwiększeniu X o 1 jednostkę oczekuje się zwiększenia decyzyjnej zmiennej y o b₁ jednostek.

Wartość współczynnika regresji b₁ w równaniu 15 wskazuje nam, że przy zwiększeniu zmiennej o 1 jednostkę i przy pewnej stałej wartości X₂ oczekuje się zwiększenia średniej decyzyjnej zmiennej X o b₁ jednostek.

Wartość współczynnika regresji b₂ w równaniu 15 wskazuje nam, że przy zwiększeniu zmiennej X₂ o 1 jednostkę i przy pewnej stałej wartości X₁ oczekuje się zwiększenia wartości średniej decyzyjnej zmiennej X₀ o b₂ jednostek.

Przykład.

Znaleźć liniowe równanie regresji zależności zysku firmy (+y5 zł) od inwestycji (+ y 3 zł) i ilości ludzi.

X₀ - zysk firmy

X₁ - inwestycje

X₂ - ilość ludzi.

X0i		X1i	X2i	X1i^2	X1i ∙ X2i	X0i ∙ X1i	X2i^2	X0i ∙ X2i
1		2	5	4	10	2	25	5
2		3	7	9	21	6	49	14
1		3	6	9	18	3	36	6
3		4	8	16	32	12	64	24
4		5	9	25	45	20	81	36
3		4	8	16	32	12	64	24
5		6	10	36	60	30	100	50
∑	19	27	53	115	218	85	419	159

Równanie regresji zależności zysku od inwestycji i ilości ludzi ma postać 15 dla znalezienia parametrów b₀ , b₁ , b₂ wypisujemy układ 16.

n = 7

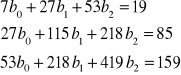
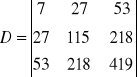
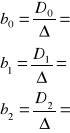
Rozwiązanie układu równań 14 ma postać:

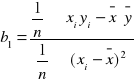
(17)

(18)

Estymetory wyrażone wzorami 17 i 18 są nazywane estygmatorami klasycznej metody najmniejszych kwadratów.

Reszta dla okresu i nazwiemy różnice między wartością empiryczną a teoretyczną zmiennej objaśnianej.

Oryginalne kryterium suma kwadratów reszt może być potraktowana jako miara dopasowanej linii regresji próby do punktu empirycznego. Zdefiniujemy wariancję zmiennej objaśnianej y_i jako róznicę:

Wtedy całkowitą wariancją jest:

(19)

Ze wzoru
otrzymujemy wzór postaci :

(20)

SST = SSR + SSE

Gdzie:

- zmienna objaśniana

- zmienna nieobjaśniana

Podzielimy stronami wzór 20 przez SST :

Mamy wtedy :

(21)

Współczynnikiem determinacji nazywamy wyrażenie:

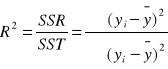
(22)

KOMENTARZ.

R² = 0 w przypadku gdy linia regresji jest równoległa do osi odcinków i wartości teoretycznej , równe są zmiennej objaśnianej:

R₂ = 0 gdy wszystkie punkty empiryczne należą do linii regresji próby co powoduje że reszta równa się 0 .

Współczynnikiem zmienności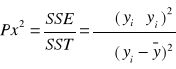
. Ze wzoru wynika, że współczynnik zbieżności jako stosunek tej części zmienności badanego zjawiska, która nie jest wyjaśniona przez zmienne objaśniające danej funkcji regresji do całkowitych zmienności zmiennej objaśnianej jest miarą także unormowaną.

0 ≤ P_xy ≤ 1

Współczynnik zbieżności określa więc jaka część zmian wartości zmiennej objaśnianej nie została wyjaśniona zmiana zmiennych objaśniających przyjętych w funkcji regresji. Im wartość P_xy² jest bliższa 0 tym oszacowana funkcja regresji jest lepiej dopasowana do wartości empirycznej zmiennej objaśnianej.

---