BADANIE TRANSFORMATORÓW

1. Badanie transformatora jednofazowego w stanie jałowym.

	Pomiary				Obliczenia
Lp.	U10	U20	I0	P0		cos 0
	[V]	[V]	[A]	[W]	-	-
1	244	78	0,059	5,5	3,13	0,382
2	232	74	0,054	5,0	3,14	0,393
3	212	68	0,048	4,0	3,12	0,399
4	184	60	0,040	3,0	3,07	0,408
5	156	50	0,033	2,0	3,12	0,438
6	124	40	0,026	1,5	3,10	0,465
7	96	32	0,020	1,0	3,00	0,521
8	64	21	0,014	0,5	3,05	0,558

Przekładnie transformatora ϑ obliczyłyśmy ze wzoru:

ϑ =

Jest to stosunek napięcia górnego do napięcia dolnego i ϑ ≥ 1!

Transformator w stanie jałowym pobiera z sieci moc czynną P₀ = U_1o I₀ cosφ₀ . Z tej zależności obliczyłyśmy cosφ₀:

cosφ₀ =

Następnie wykreśliłyśmy charakterystykę transformatora w stanie jałowym:

Badanie transformatora w stanie jałowym przeprowadza się przy stałej częstotliwości i przy regulowanym napięciu zasilania. Z charakterystyki P₀ = f(U_1o) wynika, że zmniejszenie wartości napięcia zasilania poniżej wartości znamionowej jest dopuszczalne i nie przynosi transformatorowi żadnej szkody. Natomiast zasilanie transformatora napięciem o wartości większej niż znamionowa powoduje znaczny wzrost strat mocy w rdzeniu stalowym (to może stać się przyczyną nadmiernego nagrzania i uszkodzenia fransformatora). Wzrost wartości mocy P₀ świadczy o pogorszeniu się stanu izolacji między poszczególnymi blachami lub nawet o zwarciu blach pakietu. Dla bardzo małych wartości napięcia, krzywa I₀=f(U₁₀) ma przebieg pierwiastkowy, co oznacza wzrost wartości cosφ₀ w funkcji napięcia, następnie krzywa I₀=f(U₁₀) przebiega prostoliniowo, czemu odpowiadają małe zmiany cosφ₀ i wreszcie I₀=f(U₁₀) ma przebieg zbliżony do parabolicznego, czemu odpowiadają zmiany krzywej cosφ₀=f(U₁₀) zbliżone do hiperboli. Dla niewielkiego napięcia cosφ₀ osiąga maksimum. Dla znamionowego napięcia cos φ₀ ≈ 0,1.

Wykreślona przez nas charakterystyka jest bliska charakterystyce teoretycznej, niedociągnięcia wynikają z małej ilości pomiarów i błędów pomiarowych.

Korzystając z powyższego wykresu przyjmujemy znamionowy prąd jałowy i znamionowe straty jałowe:

I_0n = 20 [mA] = 0,02 [A] P_0n = 1 [W]

Dalej obliczyłyśmy wartości parametrów gałęzi poprzecznej schamatu zastępczego:

R_Fe ≈ U_1n² / P_0n = 96² / 1 = 9216 [Ω]

X_μ ≈ U_1n / I_0n = 96 / 0,02 = 4800 [Ω]

2. Badanie transformatora jednofazowego w stanie zwarcia.

	Pomiary			Obliczenia
Lp.	U1z	I1z	Pz	cos z
	[V]	[A]	[W]	-
1	120	0,75	11	0,14
2	105	0,66	9	0,13
3	100	0,62	7,5	0,12
4	60	0,47	4,5	0,13
5	20	0,31	2,5	0,14

Współczynnik mocy cosφ_1z transformatora w stanie zwarcia jest zależności od napięcia w uzwojeniu pierwotnym stały:

cosφ_1z =

Charakterystyka dla stanu jałowego przedstawia się następująco:

Charakterystyka I_1z = f(U_1z) przebiega liniowo, gdyż przy stałych rezystancjach uzwojeń prądy są proporcjonalne do napięcia. Charakterystyka P_z = f(U_1z ) ma przebieg zbliżony do paraboli.

Następnie przeprowadziłyśmy obliczenia parametrów gałęzi podłużnej schematu zastępczego oraz procentowych napięć zwarcia:

Z_z1 ≈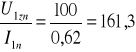

R_z1≈

X_z1 =

Δu_z% =
[%]

Δu_R% =
[%]

Δu_X% =
[%]

3. Badanie transformatora jednofazowego w stanie obciążenia przy U₁ = U_1n = 230V.

	Pomiary				Obliczenia
Lp.	I1	P1	U2	I2	P2	η	cos 1	Δu%
	[A]	[W]	[V]	[A]	[W]	-	-	%
1	0,17	36	97,75	0,4	39,1	1,09	0,92	0
2	0,19	40	87,40	0,5	43,7	1,09	0,92	11
3	0,21	43	80,50	0,6	48,3	1,12	0,90	18
4	0,23	48	75,57	0,7	52,9	1,10	0,91	22
5	0,29	62	75,30	0,8	60,2	0,97	0,93	23
6	0,39	86	74,75	1,2	89,7	1,04	0,96	24
7	0,52	114	74,75	1,6	119,6	1,05	0,95	24
8	0,65	142	74,75	2	149,5	1,05	0,95	24

U₂ =
, U₁=const.

Moc czynną P₂, oddawaną przez uzwojenie wtórne transformatora odbiornikowi obliczyłyśmy z zależności:

P₂ = U₂ * I₂

Następnie znając moc czynną P₂ i moc czynną P₁ pobieraną przez uzwojenie pierwotne transformatora w sieci można policzyć sprawność tego transformatora:

η =

Współczynnik mocy cosφ₁ obliczyłyśmy ze wzoru :

cosφ₁ =

W naszym przypadku U_20n wynosi 97,75 [V]. Możemy więc policzyć zmienność napięcia:

Δu% =

Znając zadane wielkości wykreśliłyśmy charakterystyki obciążeniowe:

Jedną z charakterystycznych własności pracy transformatora jest zakres wahań napięcia strony wtórnej przy przejściu od stanu jałowego do obciążenia znamionowego. Wprowadzono pojęcie zmienności napięcia Δu% w transformatorze. Za względu na zmniejszanie się napięcia U₂ wraz ze wzrostem obciążenia czynnego charakterystyka Δu% = f(I₂) powoli wzrasta. Współczynnik mocy cosφ₁ ze wzrostem obciążenia czynnego I₂ rośnie. Dalsze zwiększanie prądu obciążenia I₂ powoduje niewielkie zmiany współczynnika mocy cosφ₁. W stanie obciążenia transformator wykazuje następującą własność : im większy prąd I₂ oddaje uzwojenie wtórne odbiornikowi, tym większy prąd I₁ pobiera uzwojenie pierwotne ze źródła napięcia. Zagięcie charakterystyki I₁ = f(I₂) tłumaczy się tym, że wraz ze wzrostem obciążenia o charakterze czynnym składowa czynna prądu pierwotnego I₁ jest dużo większa od składowej biernej.

Korzystając z charakterystyk wyznaczamy wartości η_n oraz Δu_%:

η_n =
= 0,97 Δu_%n =

i porównujemy je z:

- obliczoną wartością η_n ze wzoru:

η_n =

- obliczoną wartością Δu_R% = 25,32[%]

Otrzymujemy:

- nieznaczną różnicę wyznaczonego η_n do obliczonego (0,97 > 0,9);

- dużą różnicę dla Δu_% (Δu_%n = 23% ≈ Δu_R% = 25,32%).

Strona5

---