UKŁAD WSPÓŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH ( 0,0,0)
PUNKT TEN POKRYWA SIĘ Z POCZĄTKIEM UKŁADU WSPÓŁRZĘDNYCH
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( X,0,0)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OXZ
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
= 00°
λ = OO° JEŻELI X > 0
λ = 180° JEŻELI X < 0
H = | X | - a
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( O,Y, O)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OZY
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
= 00°
λ = 9O° JEŻELI Y > 0
λ = - 90° JEŻELI Y < 0
H = | Y | - a
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( O, O, Z)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OZ
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
λ - NIEOKREŚLONA
ϕ = 90° JEŻELI Z > 0
ϕ = - 90° JEŻELI Z < 0
H = | Z | - b
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( X, Y, 0)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OXY
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
ϕ = 00°
tg λ =![]()
(a + H)2 = X2 + Y2
H = ![]()
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( X, 0, Z)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OXZ
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
λ = 00° , jeżeli x > o
λ = 180° , jeżeli x < o
tg ϕ= ![]()
gdzie r =![]()
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( 0, Y, Z)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OYZ
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
λ = 90° , jeżeli Y > o
λ = -90° , jeżeli Y< o
tg ϕ= ![]()
gdzie r =![]()
PUNKT A O WSPOŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH
( X, Y, Z)
PUNKT TEN ZNAJDUJE SIĘ NA OSI OYZ
WSPÓŁRZĘDNE GEODEZYJNE PUNKTU A WYNOSZĄ
tg λ = ![]()
tg ϕ= ![]()
gdzie r =![]()
PRZEKROJE GŁÓWNE ELIPSOIDY
Przez dowolny punkt (A) powierzchni elipsoidy można poprowadzić prostą prostopadłą /normalną / do powierzchni. Płaszczyzny zawierające normalną przecinają powierzchnię elipsoidy w nieskończenie wielu krzywych zbiegających się w punkcie A.
Płaszczyznami normalnymi nazywa się płaszczyzny zawierające w danym punkcie normalną (prostopadłą ) do elipsoidy .
Przekrojami normalnymi nazywa się krzywe uzyskane na powierzchni elipsoidy w wyniku przecięcia jej płaszczyznami normalnymi ( zawierającymi normalną )w danym punkcie do elipsoidy.
Wśród nieskończenie wielu przekrojów normalnych elipsoidy wyróżnia się dwa przekroje główne
Przekroje główne są to przekroje, których płaszczyzny normalne tworzą z sobą kąt prosty, a z otrzymanych krzywych na powierzchni elipsoidy , jedna ma krzywiznę największa a, druga zaś najmniejszą w punkcie A.
Jednym z przekrojów głównych jest przekrój południkowy / południk punktu A/, a drugim przekrój prostopadły do południka, zwany pierwszym wertykałem lub przekrojom poprzecznym.
Rys. Przekroje główne elipsoidy
Krzywizna przekroju południkowego jest największa, tj, promień krzywizny jest najmniejszy. Natomiast krzywizna pierwszego wertykału jest najmniejsza, tj, promień krzywizny jest największy.
Przekroje normalne, zawarte pomiędzy przekrojami głównymi mają krzywizny i promienie pośrednio. Są to przekroje normalne dowolne (skośne)
Promień krzywizny przekroju południkowego M :
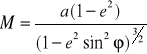
Promień równoleżnika z twierdzenia Meusniera :jeżeli płaszczyzna przekroju poprzecznego i płaszczyzna równoleżnika tworzą ze sobą kąt równy szerokości geodezyjnej i maja wspólną styczna do równoleżnika w punkcie A , to promień równoleżnika jest równy iloczynowi promienia krzywizny tego przekroju poprzecznego i cosinusa szerokości
normalna
A
r = N cos ϕ
jak i promień równoleżnika można wyliczyć w funkcji szerokości
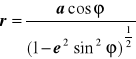
stad:
promień krzywizny przekroju poprzecznego N:
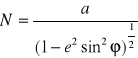
W obu biegunach promienie krzywizny wszystkich przekrojów normalnych są sobie równe i wynoszą:
![]()
Długość łuku południka i równoleżnika elipsoidy
Dla małej różnicy szerokości geodezyjnych długość łuku elipsy południkowej między dwoma punktami wyraża się wzorem uproszczonym
d= Mś (ϕB - ϕA )
Gdzie:
Mś - promień krzywizny południka dla szerokości średniej punktów
Równoleżniki elipsoidy obrotowej są kołami ,których płaszczyzny są prostopadłe do osi obrotu ,a promień r każdego z równoleżników można wyliczyć wzorem:
r = N cosϕ
Tak więc obliczając długość równoleżnika a zawartą między dwoma południkami o określonych długościach geodezyjnych λ A, λB
a = r (, λB - λ A )
a =Δλ r = N cosϕ
![]()
![]()
- współczynnik zamiany miary łukowej na stopniową
LINIA GEODEZYJNA A ORTODROMA
Linia geodezyjna - krzywa mająca tę własność , że w każdym jej punkcie normalna przeprowadzona do jej powierzchni leży w płaszczyźnie ściśle stycznej tej krzywej , jest to krzywa , której krzywizna geodezyjna równa się zeru.
Linia geodezyjna to najkrótsza linia łącząca dwa punkty na danej powierzchni. Przez dwa punkty , w niektórych przypadkach może przechodzić nieskończenie wiele linii geodezyjnych . O linii geodezyjnej mówimy gdy rozpatrujemy odległość na elipsoidzie.
Ortodroma - krótszy łuk koła wielkiego. Odległość po ortodromie jest najkrótszą odległością między dwoma punktami na powierzchni kuli.
Mówiąc o ortodromie , rozpatrujemy linię na kuli, choć wyliczenia przeprowadzamy z uwzględnieniem parametrów elipsoidy np. powiększona szerokość
Iloczyn promienia równoleżnika danego punktu i sinusa azymutu linii geodezyjnej w tym punkcie jest wielkością stałą dla każdego punktu
r sin α = const
8
A
A
a
λ
H
Y
Z
X
O
X
Z
0
O
a
Z
λ =90
Y
H
A
X
a
λ
A
b
H
A
0
O
a
A
Y
H
Z
X
O
Z
ϕ
Z
λ
X
Y
![]()
a
Y
X
a+ H
X
Y
λ
H
Z
A
O
a
r
λ
Y
X
A
X
Z
ϕ
Z
a
H
A
0
O
a
A
Y
λ
λ =90
X
ϕ
ϕ
![]()
λ
ϕ
H
Y
Y
X
X
λ
X
r
Y
Z
b
r
N
ϕA
ϕB
A
B
M
OM
d
Δλ
λ A
λB
N
r
ϕ
a
Wyszukiwarka
Podobne podstrony:
7916
7916
7916
7916
7916
7916
praca-magisterska-wa-c-7916, Dokumenty(2)
7916
więcej podobnych podstron