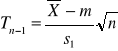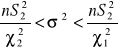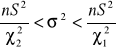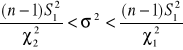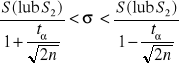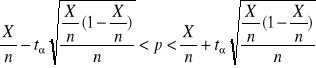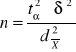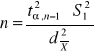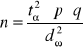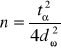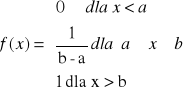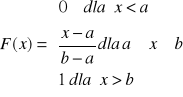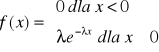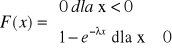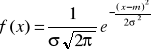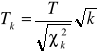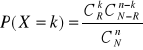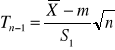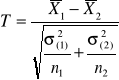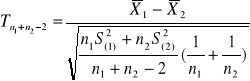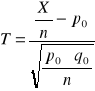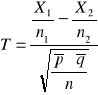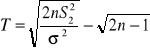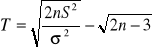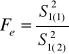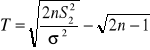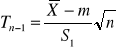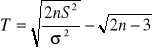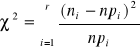ESTYMACJA PRZEDZIAŁOWA
Przedział ufności dla wartości przeciętnej m |
||
|
1
|
|
|
2 |
|
Przedział ufności dla wariancji |
||
1-α- poziom ufności dQ- bezwzględny błąd losowy (max błąd szacunku)- połowa przedziału ufności B(Q)- wzgłędny błąd losowy, względna precyzja ω=X/n- częstość występowania sukcesu Estymatory:
-nieobciążoność
-obciążenie estyma:
-asymptot nieobciąż
-jeżeli estymator jest nieobciążony (lub asympt nieo) i spełnia -estymator nieobciążony o najmniejszej wariancji jest najefektywniejszy - jeśli jest nieobciążony:
- -to wyżej/Q-względny średni błąd szacunku -1/sqrt(V(Q))- precyzja szacunku |
1 |
dla k=n |
|
2 |
dla k=n-1 |
|
3 |
|
Przedział ufności dla wskaźnika struktury (prawdopodobieństwa sukcesu, procentu, odsetka, frakcji) |
||
|
||
Minimalna liczebność próby: |
|
Dla oszacowania m |
|
|
|
|
|
Dla oszacowania p |
|
p- znane lub n>100→p=ω |
p- nieznane to p=0.5 |
|
|
ROZKŁADY ZMIENNEJ LOSOWEJ
CIĄGŁEJ |
SKOKOWEJ |
r. jednostajny [a,b]
|
r. zero-jedynkowy EX=np VX=pq
E(C)=C E(CX)=CE(X) E(X+Y)=E(X)+E(Y) E(X-Y)=E(X)-E(Y) E(Σxi)=ΣE(xi) V(C)=0 V(CX)=C2E(X) V(Σxi)=ΣV(xi)
|
r. wykładniczy
EX= |
r. dwumianowy EX=np VX=npq
gdy p<0.2 i n>100- przybliżamy r. Poissona
gdy n>30- przybliżamy r. normalnym X-N(np., |
r. normalny
EX=m VX= |
|
|
r. Poissona
EX=m VX=m |
r. chi-kwadrat
k>30⇒ |
r. geometryczny
|
r. studenta
|
r. hipergeometryczny
N-liczba el. W populacji R-liczba el majacych wyróżnioną cechę w populacji n- liczebność próbki k- liczba sukcesów (wyr elw próbce |
Statystyki z próby:
![]()
![]()
![]()
![]()
![]()
Test stosunku wiarogodności:
![]()
![]()
Statystyka testowa:![]()
-nie znamy rozkładu. Jeżeli próba duża to rozkład ![]()
zbiega do rozkładu chi-kwadrat o 1 stopniu swobody
Zbiór krytyczny Z jest prawostronny: ![]()
|
Warunki |
Sprawdzian hipotezy |
Wartość krytyczna |
|||||
WARTOŚĆ PRZECIĘTNA H0:m=m0 H1:m≠m0 H1:m>m0 H1:m<m0 |
σ znane, n<30 σ znane, n>30 σ nieznane, n>30 (σ=S) |
rozk:N(0,1) |
zb. dwustronny
zb. jednostronny |
|||||
|
σ nieznane n<30 |
rozk. Studenta o n-1 st. swo |
zb. dwustronny
zb. jednostronny |
|||||
DWIE WARTOŚCI PRZECIĘTNE H0:m1=m2 H1:m1≠m2 H1:m1>m2 H1:m1<m2 |
σ1,σ2 znane n1<30 n2<30 σ1,σ2 znane n1>30 n2>30 σ1,σ2 nieznane n1>30 n2>30 |
rozk: n(0,1)
|
zb. dwustronny
zb. jednostronny |
|||||
|
σ1,σ2 nieznane n1<30 n2<30, σ1=σ2 (Jeśli nie wiemy, czy σ1=σ2 to należy zweryfikować hipotezę o dwóch wariancjach H0:σ12=σ22) |
|
zb. dwustronny
zb. jednostronny |
|||||
WSKAŹNIK STRUKTURY H0:p=p0 H1:p≠p0 |
|
|
zb. dwustronny
zb. jednostronny |
|||||
DWA WSKAŹNIKI STRUKTURY H0:p1=p2 H1:p1≠p2 |
n1>100, n2>100
|
|
zb. dwustronny
zb. jednostronny
|
|||||
WARIANCJA H0:σ2=σ02 H1:σ2>σ02 (Zwykle prawostronny zbiór krytyczny) |
m znane n<30 |
rozk χ2 z n st swob |
|
|||||
|
m nieznane n<30 |
rozk χ2 z n-1 st swob |
|
|||||
|
m znane n>30 |
rozk: N(0,1) |
zb. dwustronny
zb. jednostronny |
|||||
|
m nieznane n>30 |
rozk: N(0,1) |
|
|||||
DWIE WARIANCJE H0:σ12=σ22 H1:σ12>σ22 |
Numerujemy tak aby |
rozk: F-Snedecora r1=(n1-1) r2=(n2-1) stopni swobody |
Jeśli Fe>Fα- odrzucamy H0
|
|||||
Dla średniej |
Dla wariancji |
|||||||
|
n<30, X-N(m,σ) |
n>30, X-dow |
|
n<30, X-N(m,σ) |
n>30, X-N(m,σ) |
|||
σ-znane |
|
|
m-znane |
|
|
|||
σ-nieznane |
dla n<10 |
|
m-nieznane |
dla n>=10
|
T-N(0,1)- roz norm Tn-1- stud o n-1 st swo χ2- chi2 o k(n lub n-1) st swob |
|||
Lemat Neumanna-Pearsona:
Zbiór odrzucenia hipotezy H0:
α= P(zbiór odrzucenia)(0,06)+pi*P(granica)
made by sheep®
|
TESTY ZGODNOŚCI:
Chi-kwadrat |
rozk: χ2 k=(r-s-1) st swob r- liczba przedziałów klasowych s- liczba wstępnie estymowanych parametrów
chie>chiα- odrzucamy H0 |
szereg rozdzielczy X-N(m,σ)
0.5-Φ(- ti1) gdy ti1<0 F(ti1)= 0.5 gdy ti1=0 0.5+Φ( ti1) gdy ti1>0 p1=F(ti1) pi=F(ti1)-F(t(i-1)1) pr=1-F(t(r-1)1) |
λ- Kołmo |
|
z tablic F(ti1) jak wyżej λe<λα- nie ma podstaw do odrzucenia |
Kołmo-Smirn |
rozk:λ-Kołmogorowa |
z tablic λe<λα- nie ma podstaw do odrzucenia H0
|
ESTYMACJA PUNKTOWA:
-nierówność Rao- Cramera 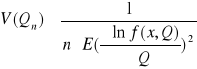
-efektywność estymatora 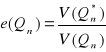
-metoda największej wiarygodności ![]()
![]()
INNE:
-wniosek z tw.M-L gdy ![]()
, ![]()
, ![]()
to ![]()
, n>30
-CTG Zn=X1+...+Xn to ![]()
-wniosek z CTG jeśli ![]()
to ![]()
, n duże
Przybliżenia normalnym:
-suma o różnych rozkładach normalnych:
![]()
-różnica różnych ![]()
-różnica jednakowych ![]()
-średnia różnych ![]()
Rozkład różnicy średnich arytmetycznych z n-elementowych prób z populacji normalnych ![]()
![]()
-m1,m2 znane, σ1,σ2 znane 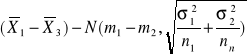
-m1,m2 znane, σ1,σ2 jednakowe, nieznane
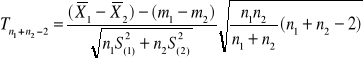
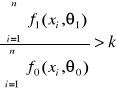
![]()
, ![]()
, ![]()
Wyszukiwarka
Podobne podstrony:
kartka ze wzorami ekonometriaSS Nieznany
ekonomika - 3 kartka ze wzorami, Norma techniczna
ekonomika - 1 kartka ze wzorami, Procent prosty
ekonomika - 2 kartka ze wzorami, Wskaźnik kosztu własnego produkcji 1m3 drewna na pniu
Kartka2, !Archiwalne, I Rok, Semestr II, Metody Numeryczne I, Kartki ze wzorami
opracowanie pytań na wykład ze statystyki, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie
SPSS paca domowa 1 odpowiedzi, Studia, Kognitywistyka UMK, I Semestr, Statystyczna analiza danych
dom0, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Kopia Opis techniczny B, Skrypty, UR - materiały ze studiów, studia, studia, 4 STASZEK, Semestr II,
pytania ze zdrowia, Studia, Psychologia, SWPS, 3 rok, Semestr 05 (zima), Psychologia Zdrowia
zapotrzebowanie, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr
crossgosp, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR V, Woi
ściana2, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
ściana3, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
dom1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Estzad, Studia, Przetwórstwo mięsa - Semestr 1, Statystyka, materiały na egzamin
kubaturap, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, N
Cwicz1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VIII, Bud
więcej podobnych podstron