Laboratorium Wytrzymałości Materiałów |
||
WMRiP Grupa M5 Rok II Semestr IV Nr podgrupy I
Posadzy Piotr Walkowiak Daniel Winiecki Mariusz Wróblewski Adam Wróblewski Paweł |
Temat: Tensometria statyczna. Naprężenia w zginanej belce. |
|
Data wykonania ćwiczenia: 1998-04-16 |
Data oddania sprawozdania: 1998-04-23 |
Ocena: |
Szkic belki.
P a
A x
C 100 b
D E
B
l
l = 700 mm
a = 350 mm
b = 5 mm
P = 5,10,15 kN
x - odległość tensometrów od podpory.
Opis stanowiska pomiarowego.
Do przeprowadzonego ćwiczenia zastosowany został układ tensometryczny
mostka Wheatstone`a z aparaturą wzmacniającą. Wykorzystany został również
układ o zwiększonej czułości: rozetę tensometryczną dwuczujnikową.
tablica z wynikami pomiarów i obliczenia.
Lp |
x [mm] |
P [kN] |
XAB |
CAB [mV/V] |
XC |
Cc [mV/V] |
εA·106 |
εB·106 |
γc·106 |
σA [MPa] |
σB [MPa] |
τc |
εc·106 |
1 2 3 |
260 |
5 10 15 |
95 93 55 |
0,1 0,2 0,5 |
32 69 54 |
0,1 0,1 0,2 |
|
|
37 85,2 127,8 |
18,5 36,26 56,44 |
-18,5 -36,26 -56,44 |
11,84 22,19 34,93 |
74 138,7 218,3 |
1` 2` 3` |
200 |
5 10 15 |
36 72 44 |
0,2 0,2 0,5 |
12 59 49 |
0,2 0,1 0,2 |
|
|
0 -55,4 -133,2 |
8,14 12,96 19,98 |
-8,14 -12,96 -19,98 |
6,51 19,8 26,64 |
40,7 92,5 166,5 |
1” 2” 3” |
120 |
5 10 15 |
46 90 66 |
0,1 0,1 0,2 |
17 50 89 |
0,1 0,1 0,1 |
|
|
37 51,8 -192,4 |
11,84 25,16 15,54 |
-11,84 -25,16 -15,54 |
6,51 15,98 27,82 |
40,7 99,9 173,9 |
przykładowe obliczenie εA
gdzie:
XAB - mierzona liczba działek,
A = 100 - kalibracja zakresu,
c - zakres pomiarowy mV/V,
k = 2,15 - stała czujników,
n = 2 - ilość czynnych tensometrów,
p = 1,0056 - wartość stała.
c1=0,1 mV/V
XAB1=95
n=2
k=2,15
A=100
p=1,0056
przykładowe obliczenie γc .
Cc1=0,1 mV/V
Xc1=40
n=1
k=2,15
A=100
p=1,0056
Przykładowe obliczenie σA
σA= E·εA
E=0,2·106 MPa
εA=0,0925·10-3
σA1 = 0,2·0,0925·103=18,5 MPa
Przykładowe obliczenie τc
τc= G ·2εc
G = 80000 MPa - moduł sztywności,
εc= 0,074·10-3
τc = 80000·2·0,074·10-3 = 11,84 MPa
Obliczenie teoretycznych σ i τ
Przykładowe obliczenia:
Mg = RE · x
ΣME = P · a - RD · l = 0
RD = P · a /l
ΣF = RD - RE - P = 0
RE = P - RD
RE = P - P · a / l = P·(1 - a / l)
P = 5kN
x = 280 mm
a = 345 mm
l = 705 mm
Mg = P · (1 - a / l) · x = 714,9 Nm
Wz = 34,2 cm3
T1 = RE = 2557,2 N
Smax = 19,9 cm3
b = 5 mm
I = 171 cm4
Lp. |
Mg [Nm] |
σ [MPa] |
τ [Mpa] |
1 2 3 |
714,9 1429,8 2144,7 |
20,9 41,8 62,71 |
5,95 11,9 17,8 |
1` 2` 3` |
255,3 510,6 765,9 |
7,46 14,9 22,4 |
5,95 11,9 17,8 |
1” 2” 3” |
485,1 970,2 1445,3 |
14,2 28,4 42,6 |
5,95 11,9 17,8 |
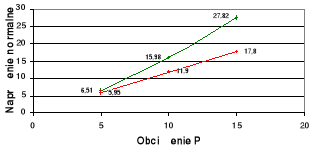
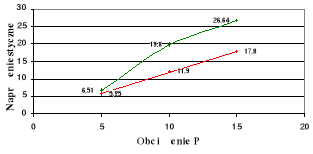
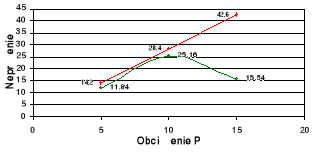
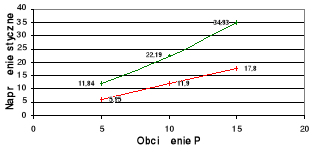
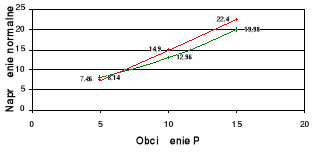
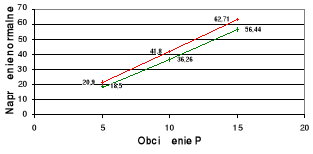
Wykresy zależności σ = σ(P) i τ = τ(P) dla poszczególnych x na tle zbieżności
teoretycznej.
wykresy teoretyczne,
wykresy doświadczalne.
x = 280
x = 100
X = 190
x = 280
x = 100
x = 190
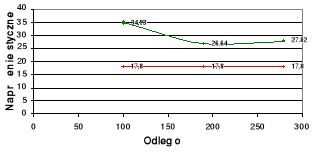
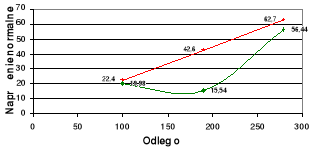
Wykresy rozkładów σ i τ na długości od 0 do a dla P = Pmax na tle rozkładów teoretycznych.
P = 15 kN
Wnioski.
Z porównania wykresów zależności σ = σ(P) i τ = τ(P) dla poszczególnych x na tle zależności teoretycznych i wykresów rozkładów σ i τ na długości od 0 do a dla P = Pmax na tle rozkładów teoretycznych wynika, że wartości wyznaczone doświadczalnie są zbliżone do wartości teoretycznych. Różnice w wartościach naprężeń mogą być spowodowane niedokładnością przyłożonej siły. Siły tej nie dało się dokładnie określić ze względu na bezwładność stosowanej aparatury. Różnice te mogą również wynikać z niedokładności pomiaru odległości usytuowania tensometrów na belce, jak również struktura materiału mogła być niejednorodna, co miało wpływ na wyniki pomiarów. Błąd mógł również wystąpić w samych obliczeniach, gdyż wzory wytrzymałościowe wykorzystywane do obliczeń opierają się na pewnych uproszczeniach.
![]()
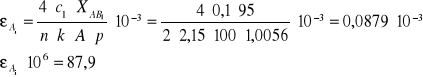
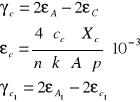
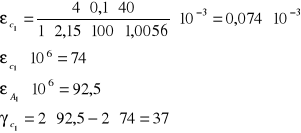
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
wytrzymalosc materialow, Szkoła Mechatronika, Semestr III, Wydyma
MATERIALOZNASTWO, Szkoła, Pollub, semestr III, KLIMEK, pytania honorata
Laboratorium wytrzymałości materiałów, ZiIP, semestr III, wydyma
zginanie wytrzymałość sprawozdanie, ZiIP, semestr III, wydyma
materiały 5, Edukacja, studia, Semestr III, Inżynieria Materiałowa, Laboratorium, Materiały 5
Napędy opracowanie ulepszone, Mechatronika, Semestr III, Napędy mechatroniczne, Napędy kolos
materialy 6, Edukacja, studia, Semestr III, Inżynieria Materiałowa, Laboratorium, Materiały 6
materialki6i9 7 8, Elektrotechnika AGH, Semestr III zimowy 2013-2014, semestr III, semestr III, Inży
więcej podobnych podstron