Politechnika Świętokrzyska w Kielcach Wydział Zarządzania i Modelowania Komputerowego
Zagadnienia Optymalizacji
Projekt nr. 2	Optymalny podział zadań między wytwórniami. Optymalizacja kosztów transportu.
Imię i nazwisko: Banak Rafał	Grupa 503	Data wykonania: 17-11-2010	Ocena	Podpis

Opis sytuacji:

Dwie wytwórnie mają produkować P=100 jednostek produktu na rok. Produkcja wymaga użycia dwóch czynników. Funkcje wytwórni mają postać:

, j=1,2

gdzie:

- zużycie czynnika 1 w j-tej wytwórni (na rok);

- zużycie czynnika 2 w j-tej wytwórni (na rok);

- roczna produkcja w j-tej wytwórni (całkowita produkcja roczna wynosi

Maksymalna zdolność przerobu wytwórni I wynosi 150 jednostek czynnika 1 na rok. Zużycie czynnika 2(
) powinno kształtować się miedzy
a
. Ponadto zachodzi, że
=1.

Maksymalna zdolność przerobu wytwórni II wynosi 140 jednostek czynnika 1 na rok. Zużycie czynnika 2(
) powinno kształtować się między 0.1
a
. Ponadto zachodzi, że
.

Koszty czynników 1 oraz 2 są odpowiednio równe

Rozwiązanie dla danych z zestawu nr.3:

Nr	a1	a2	a3
1	0.10	0.20	0.8
2	0.15	0.15	0.8
3	0.10	0.20	0.9
4	0.15	0.15	0.9
5	0.10	0.20	1.1
6	0.15	0.15	1.1
7	0.10	0.20	1.2
8	0.15	0.15	1.2
9	0.10	0.20	1.3
10	0.15	0.15	1.3

Problem 1. Dotyczy sformułowania problemu optymalnego podziału zadań między firmami.

Problem sprowadza się wyznaczenia minimum funkcji wyrażającej całkowity koszt użytych czynników, zapisanych w postaci:

Funkcja celu wyraża całkowity koszt zużytych czynników:

Podajemy punkty startowe:

x₁₁=100

x_21­=15

x₂₁=120

x₂₂=13

Minimalizację kosztów przeprowadzamy przy następujących warunkach ograniczających:

- równościowym wyrażającym, że całkowita produkcja obydwu wytwórni wynosi P

- nierównościowych nałożonych na zużycie poszczególnych czynników w każdej z wytwórni

*czynniki ograniczające:

*zakładamy, że zużycie musi być większe bądź równe 0:

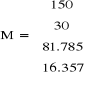
Minimalizacja funkcji celu:

Wnioski

W pierwszej wytwórni zużycie czynnika pierwszego wynosi 150 [j], natomiast zużycie czynnika drugiego 30 [j]. W drugiej wytwórni zużycie czynnika pierwszego wynosi 81.758 [j], a czynnika drugiego 16.257 [j].

Przy takim podziale produkcji minimalny jej koszt wyniesie 301.321 [j].

Warto zauważyć, że produkcja jest bardziej opłacalna w przetwórni pierwszej (mnożnik a₁=0.1). Jeśli zwiększyłaby ona zdolność przerobową czynnika 1 do poziomu 224 jednostek korzystanie z usług przetwórni 2 stałoby się nieopłacalne. Przy poziomie przerobu x₁₁=224 całkowity koszt wyniósłby 290.689 [j].

Problem 2, gdzie celem jest wyznaczenie optymalnej trasy przewozu czynnika 1 do przetwórni z trzech magazynów, przy czym zakładamy, że czynnik 1 jest dostępny w magazynie A, B, C w ilościach A - 100a₃, B - 1000a₂ , C - 120, zaś koszty przewozu są określone w poniższej tabeli.

Magazyn	A	B	C
Wytwórnia I	10	16	20
Wytwórnia II	18	14	12

Rozwiązanie

Funkcja celu jest następująca:

Podajemy punkty startowe

Rozwiązujemy problem przy następujących ograniczeniach:

- równościowym wyrażającym równość zapotrzebowania odpowiedniej wytwórni i ilości towaru sprowadzonego z poszczególnych magazynów do tej wytwórni (ilość warunków odpowiada ilości wytwórni), wartości M₀ i M₂ są wynikami minimalizacji funkcji z zadania poprzedniego;

- nierównościowych wyrażających warunek, że ilość towaru przewożonego z danego magazynu nie może być większa niż zapasy w tym magazynie (ilość warunków uzależniona jest od ilości magazynów).

Minimalizacja funkcji kosztów transportu:

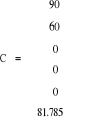
Wnioski

Dla wytwórni pierwszej czynnik pierwszy będzie dostarczany z magazynu 1 w ilości 90 [j] zaś z magazynu 2 w ilości 60 [j]. Magazyn trzeci nie będzie uczestniczył w dostawach.

Dostawy dla wytwórni 2 będą realizowane jedynie z magazynu 3 w ilości 81.785 [j].

Minimalny koszt transportu wynosi 2841.424 [j].

Warto zauważyć, że w obydwu przypadkach magazyny, z których transport jest najtańszy dostarczają najwięcej czynników. Magazyny, z których koszt transportu jest najdroższy uczestniczyłyby w dostawach jedynie wtedy, kiedy w pozostałych magazynach zabrakłoby czynników, a więc przy poziomie zapotrzebowania wytwórni 1 na poziomie większym niż 290 [j] a wytwórni 2 większym niż 320.

Należy również zauważyć, że otrzymanych ilości, które trzeba dostarczyć nie należy zaokrąglać, gdyż mogłoby to spowodować niedobór lub nadwyżkę towaru.

str. 4

---