Nazwisko i Imię (autor)
Nazwisko i Imię(kolega)
Rzeszów data
Zad1.
- wyznaczyć okres i długość fali elektromagnetycznej dla następujących częstotliwości:
a) 50 Hz i 60 Hz (częstotliwości wykorzystywane w energetyce)
b) 225 kHz (fale długie - częstotliwość nadawania programu 1)
c) 100 MHz (fale ultrakrótkie - popularne stacje radiowe)
d) 800 MHz (fale ultrakrótkie - telefonia komórkowa GSM)
e) 1,8 GHz (mikrofale - telefonia komórkowa GSM)
f) 2,5 GHz (mikrofale - sieci bezprzewodowe, kuchenki mikrofalowe)
g) 5,0 GHz (mikrofale - sieci bezprzewodowe - USA)
h) od 150 GHz do 428 THz (Tera, 10^12) - promienowanie podczerwone (cieplne)
i) od 428 THz do 750 THz - promieniowanie widzialne (światło)
![]()
![]()
T := ![]()
a)
![]()
![]()
![]()
![]()
![]()
b)
![]()
c)
![]()
![]()
d)
![]()
![]()
e)
![]()
![]()
f)
![]()
![]()
![]()
g)
![]()
![]()
h)
![]()
![]()
![]()
![]()
![]()
![]()
i)
![]()
![]()
![]()
![]()
![]()
czestotliwość |
Długość w metrach [m] |
Okres w sekundach [s] |
rozmiar systemów |
50 Hz i 60 Hz |
6*10^6; 5*10^6 |
0.017; 0.02 |
częstotliwości wykorzystywane w energetyce |
225 kHz |
1.333*10^3 |
4.444*10^-6 |
fale długie |
100 MHz |
3 |
1*10^-8 |
fale ultrakrótkie - popularne stacje radiowe |
800 MHz |
0.375 |
1.25*10^-9 |
fale ultrakrótkie - telefonia komórkowa GSM |
1,8 GHz |
0.167 |
5.556*10^-10 |
mikrofale - telefonia komórkowa GSM |
2,5 GHz |
0.12 |
4*10^-10 |
mikrofale - sieci bezprzewodowe, kuchenki mikrofalowe |
5,0 GHz |
0.06 |
2*10^-10 |
mikrofale - sieci bezprzewodowe - USA) |
od 150 GHz do 428 THz |
od 7.009*10^-7 do 2*10^-3 |
od 7.003*10^-16 Do 6.667*10^-12 |
promienowanie podczerwone |
od 428 THz do 750 THz |
od 4*10^-7 do7.009*10^-7 |
od 1.333*10^-15 do 2.336*10^-15 |
promieniowanie widzialne |
2.
- Wyznaczyć amplitudę i fazę sumy sygnałów u1 i u3, u2 i u3 oraz u1, u2 i u3 korzystając z wykresu
i danych powyżej zamieszczonych. Wyznaczyć również przesunięcie czasowe pomiędzy sygnałami składowymi a sygnałem wypadkowym oraz fazę początkową syganłów wypadkowych:
a) u1 i u3 (A1=3 V, f1=10 MHz, 1=0 rad, A3=6 V, f3=10 MHz, 3=/6 rad)
b) u2 i u3 (A2=1 V, f2=3 kHz, =/2 rad, A3=2 V, f3=3 kHz, 3=/3 rad)
c) u1, u2 i u3 (A1=3 V, f1=10 Hz, 1=0 rad, A2=6 V, f2=10 Hz, =/6 rad,
A3=4 V, f3=10 Hz, 3=0 rad)
Czy zmienia się pulsacja sygnału wypadkowego ? Odpowiedź uzasadnij.
Wskazówka!
Przesunięcia fazowe wyznaczyć "ręcznie" z wykorzystaniem narzedzia TRACE oraz wiedząc, że
=(t/T)2. Podczas wyznaczania fazy początkowej należy dodatkowo zauważyć, że u(0)=Asin( gdzie jest fazą początkową sygnału sinusoidalneg
a)
![]()
Z funkcji TRACE:
![]()
![]()
![]()
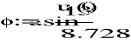
Faza początkowa:
![]()
Przesunięcie fazowe pomiędzy u1 a u13:
Przesunięcie fazowe pomiędzy u3 a u13:
b)
![]()
Faza początkowa:
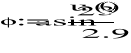
![]()
Z funkcji TRACE:
![]()
![]()
![]()
![]()
Przesunięcie fazowe pomiędzy u2 a u23:
![]()
Przesunięcie fazowe pomiedzy u3 a u23:
c)
![]()
Faza początkowa:
![]()
Z funkcji TRACE:
![]()
![]()
![]()
![]()
![]()
Przesunięcie fazowe pomiędzy u1 a u123:
![]()
Przesunięcie fazowe pomiędzy u2 a u123
![]()
Przesunięcie fazowe pomiędzy u3 a 123
Częstotliwość sygnałów składowych jest taka sama, jak częstotliwość sygnałów wypadkowych, ponieważ każdy składowy sygnał ma tą samą częstotliwość. Z tego względu pulsacja sygnału wypadkowego nie zmienia się.
ĆWICZENIA
3a) Przedstaw liczby w postaci wykladniczej i trygonometrycznej
z1:=1+i
z2:=1-2i
z3:=-4+3i
z4:=4i
3) Arytmetyka liczb zespolonych
- Wyznaczanie różnych postaci liczb zespolnych
- dodawanie, odejmowanie, mnożenie liczb zespolonych
3b) Przedstaw liczby zespolone w postaci kartezjanskiej
z1:=5e-j30
z2:=2.83ej45
z3:=3e-jpi/2
z4:=2ej75
3c) Podaj liczby sprzężone do podanych (w Mathcadzie z*=>z" )
z1:=3-2i
z2:=-5+5i
z3:=-4-i
3d) Wyznacz sume, różnice, iloczyn oraz iloraz liczb zespolonych
A) z1:=2+3i z2:=z1*
B) z1:=2+3i z2:=z1
C) z1:=3+3i z2:=1-1i
D) z1:=-2+1i z2:=2-1i
E) z1:=-2-2i z2:=4-3i
Wyniki przedstaw w postaci kartezanskiej i trygonometrycznej
W sprawozdaniu przedstawić wyniki na płaszczyźnie zespolonej
A1)
![]()
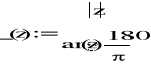
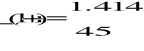
![]()
![]()
A2)
![]()
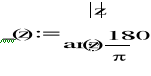
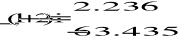
![]()
![]()
A3)
![]()
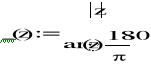
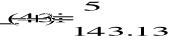
![]()
![]()
A4)
![]()
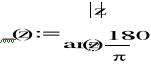
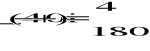
![]()
![]()
B1)
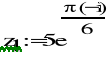
![]()
![]()
![]()
![]()
B2)
![]()
![]()
B3)
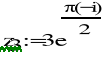
![]()
![]()
![]()
![]()
B4)
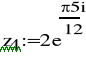
![]()
![]()
![]()
![]()
C1)
![]()
C2)
![]()
C3)
![]()
D1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D4)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D5)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D3)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zad4)
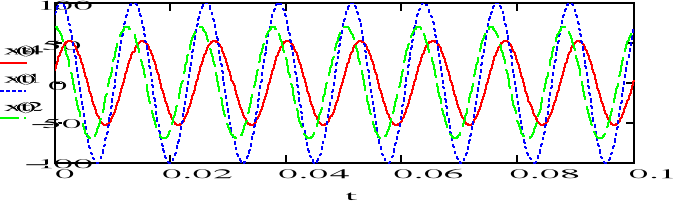
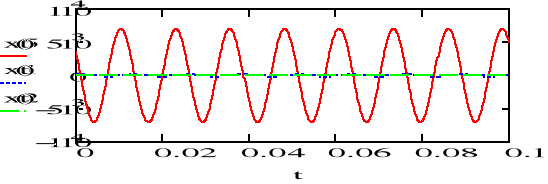
Wykorzystując metodę symboliczną należy wyznaczyć sygnał x3 na podstawie sygnałów x1 i x2 jeśli:
x3=x1+x2; x3=x1-x2; x3=x1x2; x3=x1/x2
x1=100sin(500t+/3) oraz x2=70cos(500t)
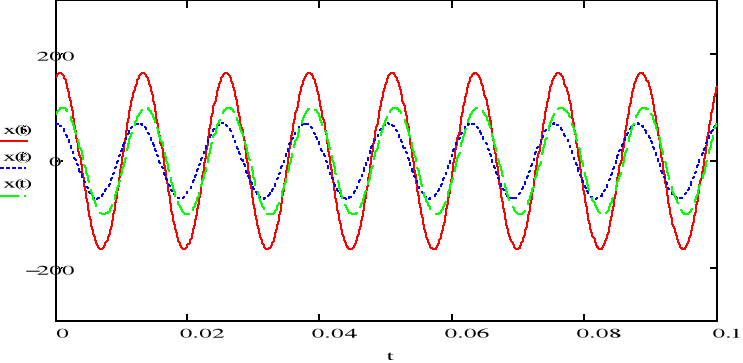
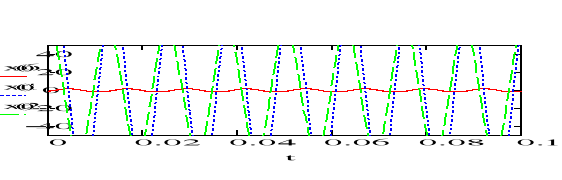
Przedstawić sygnały x3 na wykresie razem z sygnałami x1 i x2.
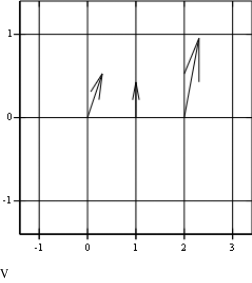
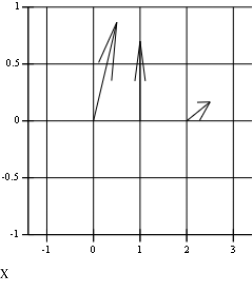
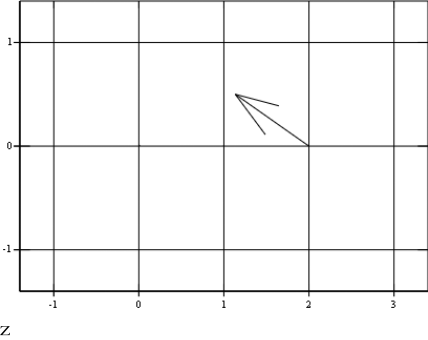
W sprawozdaniu narysować wskazy zespolone (wykresy wektorowe) sygnałów x1, x2 i x3.
Wnioski
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
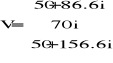
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
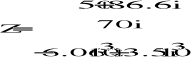
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
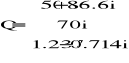
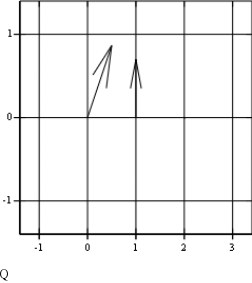
Wnioski: Jakieś napiszę.
Zad.5
5a)Przedstaw podane wielkosci fizyczne w skali logarytmicznej: [dB, dBm, dBu]
a) P=5
b) P=10mW
c)P= 35nW
5b) Przedstaw podane wielkosci fizyczne w skali logarytmicznej [dB, dBm, dBu]
a) U=15V
b) U=50mV
c)U= 23uV
5c) Oblicz wzmocnienie mocy wzmacniacza w [dB, dBm]
G=10log(P2/P1) [dB],
a) P1=3W P2=15mW
b) P1=12uW P2=40mW
c) U1=20mV U2=4V
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
157
.
0
2
10
10
42
.
1
10
445
.
1
2
7
7
7
T
t
12.6
)
(
0
123
u
asin
t
T
10
-7
7
7
2
1
.
5
10
10
2
0
.
346
2.408i
1.487
2
z
)
(
)
(
sin
i
)
(
cos
r
2
z
z
2
2.83
e
i
4
Wyszukiwarka
Podobne podstrony:
Sygnaly i systemy 2FD Linia dluga, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS Lab02 Micha 322 Kucab EF-DI1 2008 L06, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 2
Sprawozdanie nr.3 - SiS, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
LABSMO~2, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
TRAF, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS LAB05 Dawid Warchoł EF-DI1 2009 L14, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 5
LINIA, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
Transformata Z - R. Siwak, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS LAB04 Dawid Warchoł EF-DI1 2008 L14, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 4
sprawozdanie1 sis, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 1
PARTI1, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
wiczenie 4, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
ZET, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
SiS LAB03 Dawid Warchoł EF-DI1 2008 L14, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
sprawozdanie3, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 3
Transformata Laplace, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 4
Sygn&Sys sem3 C2-Rownanie stanu, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
Sprawozdanie 2, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 2
Filtracja i modulacja-spr, Studia, Semestr 1, Sygnały i Systemy, Sprawozdania
sygnały, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 1
więcej podobnych podstron