POLITECHNIKA WROCŁAWSKA

WYDZIAŁ GÓRNICZY

GEOINFORMATYKA

TEMAT: OBLICZENIE OSIADANIA PUNKTÓW PODŁOŻA BUDOWLANEGO Z UWZGLĘDNIENIEM RÓŻNYCH WARUNKÓW GRUNTOWO - WODNYCH.

PROWADZĄCY ĆWICZENIA:

DR INŻ. KRYSTYNA SZCZEŚNIAK

WYKONAŁ:

WOJCIECH IWAŚKÓW

WROCŁAW 29.03.2002

1. WSTĘP

Obiekt stanowi obszar o wymiarach 26x16x10 [m] (długość x szerokość x głębokość) oraz obciążenie ciągłe o wartości q = 150 kPa i wymiarach: 8 x 6 [m].

Podłoże tworzą ( w kolejności):

• glina piaszczysta (G_p) o miąższości 5,0 [m],

• piasek drobny (P_d) o miąższości 7,0 [m],

• glina (G) o miąższości 15,0 [m].

Ponadto na głębokości 11,0 [m] znajduje się zwierciadło wody gruntowej.

Na podstawie wyników badań i charakterystyki geologicznej gruntów podłoże zostało podzielone na warstwy geotechniczne. Dla każdej warstwy ustala się niezbędne do obliczeń wartości parametrów geotechnicznych.

Do ustalenia parametrów geotechnicznych stosuje się metody: A, B oraz C. W naszym przypadku wykorzystamy metodę B, która polega na oznaczeniu wartości parametru na podstawie ustalonych zależności korelacyjnych między parametrami fizycznymi lub wytrzymałościowymi a innym parametrem (np. I_L lub I_D) wyznaczanym metodą A (bezpośrednie oznaczenie wartości parametru za pomocą polowych lub laboratoryjnych badań gruntu).

PARAMETRY GEOTECHNICZNE

NAZWA GRUNTU	STOPIEŃ ZAGĘSZCZENIA/ STOPIEŃ PLASTYCZNOŚCI (ID / IL)	EDOMETRYCZNY MODUŁ ŚCIŚLIWOŚCI PIERWOTNEJ M0 [kPa]	EDOMETRYCZNY MODUŁ ŚCIŚLIWOŚCI WTÓRNEJ M [kPa]	GĘSTOŚĆ OBJĘTOŚCIOWA GRUNTU ρ [g/cm^3]	CIĘŻAR OBJĘTOŚCIOWY GRUNTU γ [KN/m^3]	GĘSTOŚĆ WŁASCIWA SZKIELETU GRUNTU ρS [g/cm^3]	WILGOTNOŚĆ NATURALNA wn [%}
GLINA PIASZCZYSTA GP	0,3	23 000	38 33 3	2,1	21,0	2,67	17
PIASEK DROBNY PD	0,,75	90 000	112 500	1,7	17,0	2,65	5
GLINA G	0,1	37 500	62 500	2,15	21,5	2,67	16

Parametry geotechniczne zostały odczytane wg normy: PN-81 B-03020.

Edometryczne moduły ściśliwości pierwotnej i wtórnej zostały określone przy pomocy wskaźnika skonsolidowania gruntu:

2. SCHEMATY OBLICZENIOWE, ZAŁOŻENIA DO OBLICZEŃ.

Ośrodek gruntowy uważa się za półprzestrzeń, która jest ograniczona od góry płaszczyzną poziomą (powierzchnią terenu) i rozciąga się nieskończenie głęboko i szeroko. Ośrodek gruntowy jest sprężysty (liniowo - odkształcalny), izotropowy i jednorodny.

Zasada superpozycji - w przypadku działania kilku sił Q naprężenie w dowolnym punkcie M wyznacza się jako sumę naprężeń powstałych od działania każdej z sił osobno. Obciążenie ciągłe q na półprzestrzeni można z pewnym przybliżeniem rozpatrywać jako sumaryczne działanie zastępczo wyznaczonych sił skupionych.

Naprężenia istniejące w gruncie od ciężaru wyżej leżących warstw nazywamy pierwotnymi (bytowymi) i oznaczamy symbolem σ_Zρ.

Wyznaczenie naprężeń pierwotnych.

Wartości naprężenia σ_Zρ wyznaczamy ze wzoru:

gdzie:

γ_i - ciężar objętościowy gruntu w każdej warstwie i,

h_i - grubość poszczególnych warstw i.

Przykładowy schemat obliczeniowy:

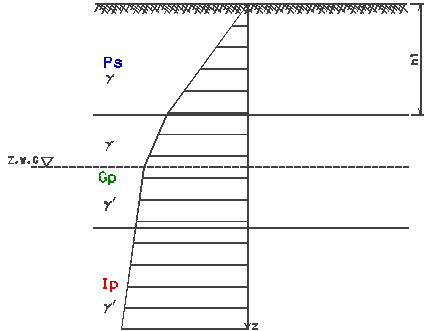
Obliczenia:

dla z = 0 [m]

dla z = 5 [m]

dla z = 11 [m]

dla z = 12 [m]

dla z = 27 [m]

Rozkład naprężeń w gruncie od działania obciążenia ciągłego.

Wyznaczanie naprężenia
metodą punktów narożnych - metodę tą stosuje się do wyznaczania naprężenia
w punkcie A, spowodowanego działaniem obciążenia q równomiernie rozłożonego na obszarze prostokątnym 1368, gdy punkt A jest położony wewnątrz tego obszaru.

Korzystając ze wzoru

gdzie:

- odprężenie spowodowane wykopem,

η_n - współczynnik rozkładu naprężenia w podłożu,

q - wartość naprężenia pierwotnego w poziomie dna wykopu,

, naprężenie
w punkcie A oblicza się jako sumę naprężeń wywołanych działaniem obciążenia q na obszarach prostokątnych mających wspólne naroże w punkcie A: 124A, 23A5, 4A67, A578.

Współczynnik η_n został wyznaczony wg wzoru:
( wyznaczenie wartości η_n jest możliwe również przy pomocy nomogramu).

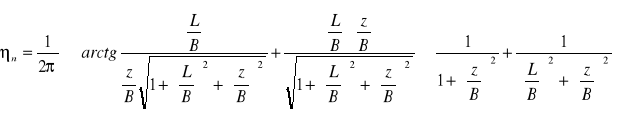
gdzie:

L - dłuższy bok prostokąta,

B - krótszy bok prostokąta,

z - zagłębienie mierzone od poziomu posadowienia.

Przykładowe obliczenia - naprężenia od odciążenia wykopem:

dla z = 0 [m] (dno wykopu)

dla z = 1[m]

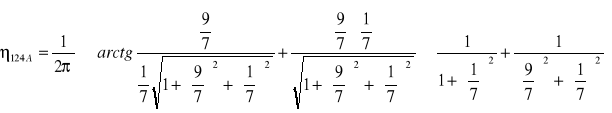
0,2496

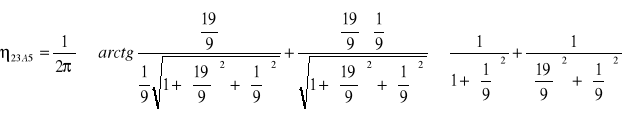
0,2498

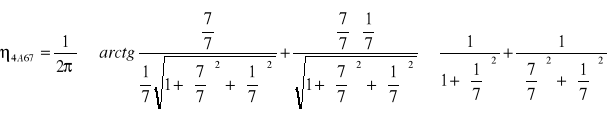
0,2495

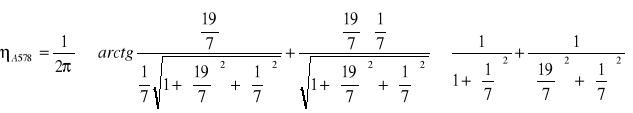
0,2497

189,73 [kPa]

z [m]	η124A	η23A5	η4A67	ηA578	η	[kPa]
1	0,2496	0,2498	0,2495	0,2497	0,9986	189,73
2	0,2470	0,2488	0,2460	0,2477	0,9895	188,00
3	0,2409	0,2463	0,2381	0,2430	0,9683	183,97
4	0,2311	0,2421	0,2258	0,2356	0,9346	177,57
5	0,2184	0,2360	0,2102	0,2259	0,8905	169,19
6	0,2037	0,2285	0,1929	0,2148	0,8399	159,58
7	0,1881	0,2199	0,1752	0,2029	0,7861	149,35
8	0,1726	0,2105	0,1581	0,1909	0,7321	139,09
9	0,1576	0,2007	0,1422	0,1792	0,6797	129,14
10	0,1436	0,1908	0,1277	0,1679	0,6300	119,70
11	0,1306	0,1809	0,1147	0,1573	0,5835	110,86
12	0,1188	0,1714	0,1032	0,1473	0,5407	102,73
13	0,1082	0,1621	0,0930	0,1380	0,5013	95,24
14	0,0987	0,1532	0,0840	0,1294	0,4653	88,40
15	0,0901	0,1448	0,0761	0,1213	0,4323	82,13
16	0,0825	0,1368	0,0692	0,1139	0,4024	76,45
17	0,0765	0,1293	0,0630	0,1070	0,3758	71,40

Wyznaczenie naprężenia σ_zq metodą punktów środkowych.

Naprężenie σ_zq od obciążenia q równomiernie rozłożonego na obszarze prostokątnym o wymiarach L×B, oblicza się ze wzoru:

gdzie:

- współczynnik rozkładu naprężenia w podłożu,

q - wartość obciążenia jednostkowego ( q = 150 kPa),

Współczynnik η_m został wyznaczony wg wzoru:

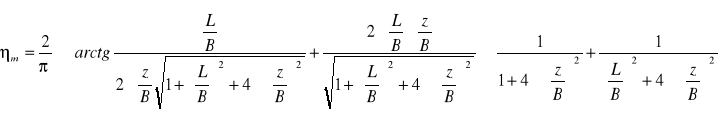
gdzie:

L - dłuższy bok prostokąta,

B - krótszy bok prostokąta,

z - zagłębienie mierzone od poziomu posadowienia.

gdzie:

- naprężenia od obciążenia budowlą,

- naprężenia wtórne,

- naprężenia dodatkowe.

Ponieważ:
≤
(150 kPa ≤ 190 kPa)

=

= 0

Przykładowe obliczenia:

dla z = 0 [m]

dla z = 1 [m]

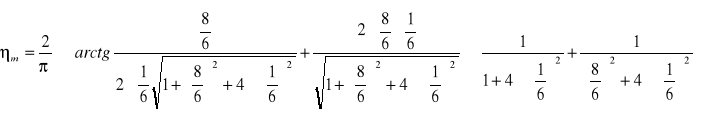
0,9822

z	η
1	0,9822	147,324
2	0,8945	134,168
3	0,7584	113,753
4	0,6190	92,844
5	0,4989	74,841
6	0,4029	60,431
7	0,3280	49,207
8	0,2701	40,515
9	0,2250	33,755
10	0,1897	28,449
11	0,1616	24,237
12	0,1390	20,856
13	0,1207	18,109
14	0,1057	15,854
15	0,0932	13,984
16	0,0828	12,418
17	0,0740	11,096

3. OBLICZENIE OSIADAŃ - PRZEMIESZCZEŃ KOŃCOWYCH.

Osiadaniem fundamentu nazywa się pionowe przemieszczenie fundamentu wskutek ściśliwości obciążonego podłoża.

Obliczenie osiadań metodą odkształceń jednowymiarowych jest oparte na następujących założeniach:

• bryła odkształcającego się podłoża gruntowego jest ograniczona u góry podstawą fundamentu, z boków pionowymi powierzchniami, przechodzącymi wzdłuż dolnych krawędzi podstawy fundamentu, od dołu kończy się na poziomie (strefa aktywna), gdzie spełniony jest warunek:

• osiadanie podłoża jest sumą osiadań poszczególnych warstw zawartych w bryle ściśliwej,

• osiadanie poszczególnych warstw wyznacza się przyjmując, że naprężenia w nich są równomiernie rozłożone i są równe maksymalnym wartościom naprężeń pod środkiem fundamentu (naprężenia środkowe),

• odkształcenia poszczególnych warstw oblicza się posługując się edometrycznymi modułami ściśliwości gruntu M_o, a więc w warunkach niemożliwej rozszerzalności bocznej warstw,

Wzór do obliczenia osiadania (zmniejszenia się grubości) pojedynczej warstwy podłoża wyprowadza się bezpośrednio ze wzoru na moduł ściśliwości edometrycznej ( w warunkach niemożliwej bocznej rozszerzalności gruntu):

Przyjmując s = Δh, mamy:

gdzie:

s - osiadanie pojedynczej warstwy,

Δσ - przyrost naprężenia,

h - grubość warstwy,

M - moduł ściśliwości (edometrycznej) danej warstwy.

Biorąc pod uwagę, że grunt został odciążony w czasie wykonywania wykopu i że podczas budowy jest wtórnie konsolidowany w zakresie wtórnych naprężeń, a więc i przy module ściśliwości wtórnej, osiadanie warstwy należy obliczać ze wzoru:

gdzie:

- naprężenie wtórne w poziomie środka danej warstwy,

- grubość danej warstwy,

- naprężenie dodatkowe,

- moduł ściśliwości wtórnej,

- moduł ściśliwości pierwotnej.

Osiadanie fundamentu wyznacza się jako sumę pionowych odkształceń poszczególnych warstw, zalegających w ściśliwym podłożu budowli, przy założeniu niemożliwej bocznej rozszerzalności:

Podłoże dzieli się na warstwy nie grubsze niż 0,5B; każda warstwa powinna być jednorodna.

Schemat obliczeniowy:

Przykładowe obliczenia osiadań:

W związku z tym, że :

≤
(150 kPa ≤ 190 kPa)

=

= 0

,będą występowały jedynie osiadania wtórne:

dla warstwy piasku drobnego (P_d):

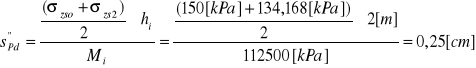
dla warstwy gliny (G)

( miąższość = 15 m, h_i≤ 3m ⇒ pięć warstewek obliczeniowych G₁...G₅):

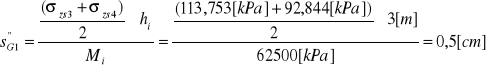
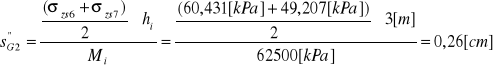
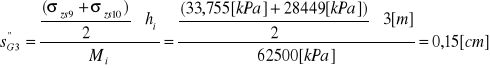
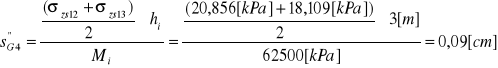
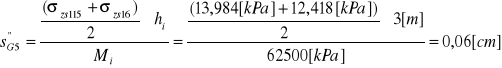
Osiadanie warstwy podłoża wynosi:

4. OMÓWIENIE WYNIKÓW I WNIOSKI

Sprawdzenie II stanu granicznego należy wykonywać dla wszystkich obiektów, które nie są posadowione na skałach litych. Jednak w niektórych przypadkach obliczeń tych można nie przeprowadzać, tj. gdy:

1. budowlą jest:

• budynek przemysłowy i magazynowy o wysokości do 3 kondygnacji

1. oraz gdy równocześnie w podłożu, do głębokości równej 3-krotnej szerokości największego fundamentu, występują wyłącznie:

• grunty niespoiste, z wyjątkiem piasków pylastych w stanie luźnym,

• grunty spoiste w stanie nie gorszym niż twardoplastyczny.

Biorąc pod uwagę wymiary budowli ( 8x6 m), wielkość jej osiadania (1,25 cm) i traktując ją np. jako budynek magazynowy dwukondygnacyjny zostanie spełniony warunek II stanu granicznego, tj.:




Na wartość naprężeń od obciążenia zewnętrznego miał znaczny wpływ naprężeń odciążających ( powstałych po wykonaniu wykopu). W związku z tym istnieją jedynie naprężenia wtórne.

Przy obliczaniu osiadania stosowałem się do warunku
, więc wartości z osiadania ostatniej warstwy (s = 0,06 cm) pominąłem.

MODELOWANIE PROCESÓW GEOLOGICZNO - INŻYNIERSKICH

15

WYDZIAŁ GÓRNICZY - GEOINFORMATYKA




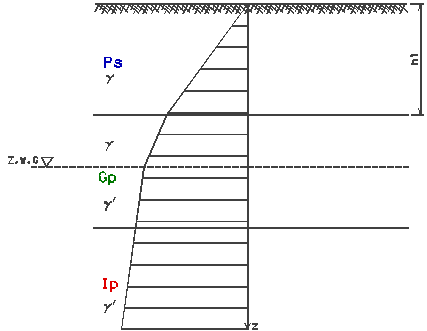
0,5 h_i

h_i ≤ 0,5 B

---